3.1. Accuracy of -Determination

The IRAS velocity field reconstructions may be produced using a variety of smoothing scales, and we have used 300 and 500 km s^-1 Gaussian smoothing. We found, however, that at 500 km s^-1 smoothing, VELMOD returned a mean _I biased high by ~ 20%; the predicted peculiar velocities were too small, and a too-large _I was needed to compensate. Our discussion from this point on will refer to 300 km s^-1 smoothing, which, as we now describe, we found to yield correct peculiar velocities and an unbiased estimate of _I.

VELMOD was run on the 20 mock catalogs, and likelihood (_forw) versus _I curves were generated for each. As with the real data (Section 4), we used the A82 and MAT TF samples only; we limited the analysis to cz 3500 km s^-1. ⁽¹⁰⁾ The curves were fitted with a cubic equation of the form

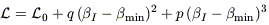
(17)

to determine _min, the value of _I for which _forw is minimized. This is the maximum likelihood value of _I. Four representative _forw versus _I plots are shown in Figure 2, along with the cubic fits. We estimate the 1 errors _± in our maximum likelihood estimate by noting the values ± _± at which = ₀ + 1. Given the presence of the cubic term in equation (17), this is not necessarily rigorous, but we can test our errors by defining the ²-like statistic

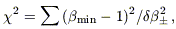
(18)

where ₊ was used if _min 1, and _- was used if _min > 1. For the 20 mock catalogs, it was found that ² = 21.2. Thus, our tests were consistent with the statement that the error estimates obtained from the change in the likelihood statistic near its minimum are true 1 error estimates. Although we formally derive two-sided error bars, the upper and lower errors differ little, and when we discuss the real data (Section 4), we will give only the average of the two. The weighted mean value of _min over the mock catalogs was 0.984, with an error in the mean of ~ 0.08 / (20)^1/2 = 0.017. Thus, the mean _min is within ~ 1 from the true answer. We conclude that there is no statistically significant bias in the VELMOD estimate of _I. The results of this and other tests that we carried out using the mock catalogs are summarized in Table 1.

TABLE 1
COMPARISON OF TRUE PARAMETERS WITH MEANS FROM VELMOD ANALYSES OF MOCK CATALOGS

Quantity	Input Value	Mock Results a	Typical Error b
I	1.0	0.984 ± 0.017	0.08
v	147	149 ± 5	20 km s-1
wLG,x c	89 ± 8	77 ± 12	54 km s-1
wLG,y c	-51 ± 10	-50 ± 14	63 km s-1
wLG,z c	-57 ± 9	-55 ± 10	45 km s-1
bA82	10.0	10.12 ± 0.08	0.36
AA82	-13.40 d	-13.44 ± 0.02	0.09
TF,A82	0.45	0.460 ± 0.006	0.026
bMAT	6.71	6.68 ± 0.05	0.22
AMAT	-5.86 d	-5.92 ± 0.02	0.09
TF,MAT	0.42	0.419 ± 0.003	0.013
a The errors given are in the mean.
b Errors in a single realization.
c Cartesian coordinates defined by Galactic coordinates.
d These true zero points differ from those reported by Kolatt et al. 1996, their Table 1, because they measured distances in units of megaparsecs, whereas we measure in units of km s-1.

Figure 2. Plots of the likelihood statistic, forw, vs. I for VELMOD runs using four of the mock catalogs. (The true value of I for the mock catalogs is unity, as discussed in the text.) Also indicated on the plots are min, the maximum likelihood values for I, and the average of its two one-sided errors ±. The solid lines drawn through the points are the cubic fits used to determine min and ±.

¹⁰ The real data analysis extended only to 3000 km s^-1, but because there are fewer nearby TF galaxies in the mock catalogs, we extended the mock analysis to a slightly larger distance. Back.