6.3. What is the Value of ?

Measuring = ^0.6 / b is an important objective of velocity analysis. Of course, the more important objective is the determination of itself. There are, broadly speaking, two ways to proceed.

6.3.1. Nonlinear Analysis

One may attempt to break the degeneracy between and biasing by extending the gravitational instability theory to the nonlinear dynamical regime. In an earlier phase of the VELMOD project, we attempted to do this; very preliminary results of this effort were described in SW, Section 8.1.2. In brief, the IRAS reconstruction was done as described in Appendix A, but a nonlinear generalization of equation (1),

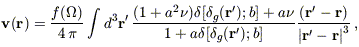
(27)

was used to derive peculiar velocities from the redshift survey density field _g. In equation (27), a = 0.28 and <²> is the mean square value of (G. Ganon et al. 1995, private communication; cf. Nusser et al. 1991). Note that the mass fluctuation is written as a generic function of _g and b, rather than simply as _g / b. This is because once we generalize to nonlinear dynamics, we must allow for the possibility of nonlinear biasing as well. There are many ways one might imagine doing this (SW, Section 2.5; Fry & Gaztañaga 1993). Generically, however, all these complications can be expanded to second order to yield a correction to equation (3):

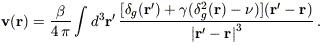
(28)

where parameterizes the combined effects of nonlinear dynamics and nonlinear biasing.

We carried out a suite of VELMOD runs using predicted peculiar velocities based on equation (28) for a range of values of , both positive and negative. Our hope was that the VELMOD likelihood statistic would be significantly lower for some value of than for the pure linear case. However, to our surprise, we found that the linear dynamics/linear biasing reconstruction ( = 0) gives the best likelihood of all. We are not certain why this is the case. Nonlinear dynamics must enter to some degree, because we know for a fact that _g is not everywhere << 1 and indeed can be quite large with our small smoothing. (Of course, we do not know whether or not nonlinear biasing is important.) Nevertheless, the small scatter between the true and IRAS-predicted peculiar velocity fields for the mock catalogs (Section 3.2) confirms that the linear IRAS velocity field, smoothed on a 300 km s^-1 scale, is a good match to actual peculiar velocities that arise from gravitational instability, at least in an N-body simulation.

A possible explanation for this seeming contradiction is as follows. Our method for predicting peculiar velocities (Appendix A) entails assigning a smooth, continuous density field from discrete redshift survey data - a procedure that takes into account the probability distribution of distance given redshift (eq. [A2]), smoothes the data with a 300 km s^-1 Gaussian, and applies a Wiener filter - and thus this reduces small-scale density enhancements. In doing so, this procedure mimics qualitatively the effects of nonlinear corrections on the velocity-density relation. The good match between the IRAS predictions and the actual peculiar velocities suggests that this mimicry is in fact fortuitously good, to the degree that formal nonlinear corrections are unnecessary. Unfortunately, if this is true, it is unlikely that nonlinear analyses will enable us to determine and b separately.

6.3.2. Constraining from Independent Estimates of b_I

The second way to estimate , given our measurement of _I, is to constrain b_I using independent information. If equation (2) with constant b holds exactly, then b_I is the ratio of the rms fluctuations of IRAS galaxies on an 8 h^-1 Mpc scale, ₈(IRAS), to the corresponding mass density fluctuations, ₈. Fisher et al. (1994a) found that ₈(IRAS) = 0.69 ± 0.04 in real space. It follows that _I can be viewed as a prediction of ₈ for a given value of :

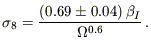
(29)

An entirely independent (although highly model-dependent) way to predict ₈ as a function of is to use COBE-normalized power spectra for a range of cosmological parameters. Liddle et al. (1996a, 1996b) have presented fitting functions that provide the normalization of CDM power spectra, in open and flat cosmologies, as a function of , , the Hubble parameter h H₀ / (100 km s^-1 Mpc^-1), and the primordial power spectrum index n, based on the four-year COBE observations (Bennett et al. 1996; Górski et al. 1996). Eke, Cole, & Frenk (1996) used these fitting functions to obtain ₈ by direct integration of the Liddle et al. power spectra and have kindly provided us with their code for doing this calculation. Thus, we may constrain ₈ by comparing the VELMOD and COBE/CDM predictions of its value and requiring that they agree to within the errors. This will be the case only for a limited range of (the "concordance range"). We emphasize, however, that the discussion to follow depends on two uncertain assumptions: first, that the CMB fluctuations measured by COBE can be reliably extrapolated down to 8 h^-1 Mpc scales, and second, that the bias parameter is scale independent from 3 to 8 h^-1 Mpc.

In Figure 20, we compare the two constraints on ₈ for a scale-invariant (n = 1) power spectrum. Figure 20a shows results for an open (i.e., = 0) universe, and Figure 20b for a spatially flat ( + = 1) universe. The COBE/CDM predictions (solid lines labeled with the values of the Hubble constant) and the constraint from equation (29) (shaded region) scale very differently with , so that the two together give strong constraints on ₈ and thus . The shaded region represents the combined VELMOD error on _I and the error in ₈(IRAS) from Fisher et al. (1994a). We do not show corresponding error regions for the COBE/CDM predictions that result from uncertainty in the COBE normalization, because the error in the predicted ₈ is in fact dominated by the allowed range of H₀, which we take to be 55 H₀ 85 km s^-1 Mpc^-1 based on a number of recent measurements (Sandage et al. 1996; Freedman 1997; Riess, Press, & Kirshner 1996; Mould et al. 1996; Tonry et al. 1997; Kundic et al. 1997).

Figure 20. Predictions of 8 as a function of for (a) open and (b) flat universes. The lines sloping up and to the right show the COBE-normalized CDM values of 8 as a function of , for four values of the Hubble constant, 55, 65, 75, and 85 km s-1 Mpc-1, under the assumption of a scale-invariant primordial power spectrum. The line sloping down and to the right shows the result from this paper, 8 = 0.69I / 0.6. The shaded region represents the 1 uncertainty in our value of I.

Figure 20 gives the following constraints for n = 1. For an open model, the concordance range is = 0.28-0.46 with the low (high) value corresponding to the highest (lowest) value of H₀ considered. For the flat model, it is = 0.16-0.34. Expressed in terms of the IRAS bias parameter, these ranges correspond to b_I = 0.92-1.38 (open) and b_I = 0.68-1.11 (flat). We also considered n 1 flat models. For example, with n = 0.9, the concordance ranges are = 0.19-0.40 and 0.21-0.45, depending, respectively, on whether tensor fluctuations are not, or are, included in the COBE normalization (Liddle et al. 1996b). The corresponding bias parameters are b_I = 0.74-1.21 and b_I = 0.80-1.29.

Two salient points follow from this comparison. First, if H₀ 60 km s^-1 Mpc^-1, the concordance range for the flat, n = 1 models requires 0.30, implying 0.70. However, studies of gravitational lensing have placed an upper limit of 0.65 at 95% confidence (Maoz & Rix 1993; Kochanek 1996), while a recent analysis of intermediate-redshift Type Ia supernovae (Perlmutter et al. 1997) indicates 0.50 at 95% confidence (both of these constraints apply when a flat universe is assumed). This contradiction constitutes evidence against a flat universe with a scale-invariant primordial power spectrum index and H₀ 60 km s^-1 Mpc^-1. If n < 1.0, one can more easily accommodate flat universes with < 0.65, provided the Hubble constant is 70 km s^-1 Mpc^-1. The second point is that the combined VELMOD and COBE/CDM predictions of ₈ are extremely difficult to reconcile with an Einstein-de Sitter universe for most reasonable values of the remaining cosmological parameters. If one assumes n 0.9, a Hubble constant 30 km s^-1 Mpc^-1, far below current observational limits, would be required for the concordance range to include = 1. Alternatively, if H₀ = 50 km s^-1 Mpc^-1, one would require a primordial power spectrum index n = 0.7 and tensor fluctuation contributions to the CMB anisotropies. Such a power spectrum index is at the lowest end of the range currently considered plausible in inflationary universe scenarios (e.g., Steinhardt 1996).

Another independent constraint on the bias parameter comes from models of structure formation that predict ₈ as a function of from the number density of locally observed rich clusters (e.g., White et al. 1993; Eke et al. 1996). The ₈() relation obtained by these authors is quite similar in form to equation (29), so we can merely test for qualitative agreement with our VELMOD results, not use it to place strong constraints on . For example, if = 0.3, equation (6.1) of Eke et al. (1996) gives ₈ = 0.85 ± 0.07, while the VELMOD result, _I = 0.492, yields ₈ = 0.70 ± 0.11. Thus, the two estimates agree to within ~ 1.2 for = 0.3; the agreement is improved for smaller . For = 1, the Eke et al. formula gives ₈ = 0.50 ± 0.04, whereas the VELMOD result yields ₈ = 0.34 ± 0.05; they disagree at about the 2.5 level. (In each case, the error bar for the comparison is obtained as the quadrature sum of the individual error bars.) A recent analysis of the cluster gas mass function (Shimasaku 1997) yields a value ₈ = 0.80 ± 0.15 that is independent of . The VELMOD result for ₈ is in good agreement with this provided 0.15 0.4.