APPENDIX B: THE RESIDUAL QUADRUPOLE

In this appendix, we calculate the expected amplitude of the velocity quadrupole generated by density fluctuations external to the IRAS sample (i.e., outside of R = 12,800 km s^-1), and internal to it, that are due to the difference between the true density field and the noisy, smoothed estimation of the density field we have from the IRAS redshift survey. The IRAS-excluded zone is another potential source of quadrupole error, but it is filled in by interpolation from regions above and below the excluded zone (Yahil et al. 1991), a procedure that agrees well with a multipole interpolation procedure based on spherical harmonics, at least for the 10° wide IRAS zone of avoidance (Lahav et al. 1994).

B1. QUADRUPOLE INDUCED BY FLUCTUATIONS BEYOND IRAS VOLUME

We express peculiar velocity in terms of a potential function (r), such that the radial component of the velocity field is given by u(r) = - / r. We will isolate the quadrupole component of this potential and calculate its angle-averaged rms contribution.

The contribution to from material at distances greater than R is given by

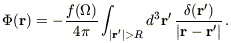
(B1)

Here is the mass, not the galaxy, density fluctuation. We now expand the denominator in the integrand in terms of spherical harmonics (e.g., Jackson 1976, eq. [3.70]) and isolate the quadrupole term to obtain

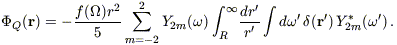
(B2)

where is the solid angle. Taking the radial component of the quadrupole velocity u_Q = -_Q / r, squaring, and averaging over the solid angle gives, after several steps of algebra,

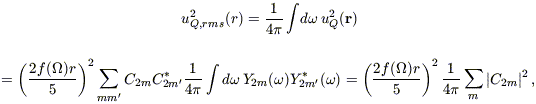
(B3)

where the last step follows from the orthonormality of the Y_lm, and for convenience we have defined the five complex coefficients

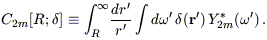
(B4)

The expectation value of |C_2m|² is independent of m, so when we take the expectation value of equation (B3), we can replace the sum with 5 × <C₂₀²>:

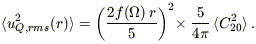
(B5)

Using the definition of Y₂₀ in terms of the second Legendre polynomial P₂ in equations (B4) and (B5) gives

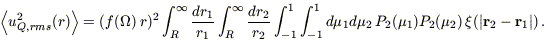
(B6)

Expressing the correlation function as the Fourier transform of the power spectrum P(k) (e.g., SW, eq. [46]) allows the integrals over r₁ and r₂ to separate. This yields

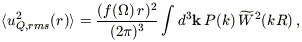
(B7)

where the kernel is given by

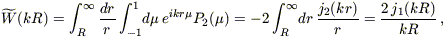
(B8)

and j_n is the nth order spherical Bessel function. A comparison of equations (B7) and (B8) with equations (37) and (38) of SW allows us to recast our result as

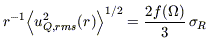
(B9)

for the expected rms quadrupole velocity on a sphere due to mass density fluctuations at distances greater than R, expressed as a fraction of Hubble flow. Here _R² is the variance in the mass overdensity within spheres of radius R. As mentioned in the text, this gives a fractional quadrupole of the order of 1%-2% for a variety of COBE-normalized power spectra.

B2. EFFECTS OF WIENER FILTERING AND SHOT NOISE

The Wiener filter operates on the Fourier transform of the IRAS density field. The final density field differs from the true density field for two reasons: the discreteness of the galaxy distribution gives rise to shot noise, and the Wiener filter, while suppressing shot noise, also suppresses the density field itself. We calculate the contribution to the quadrupole from both effects.

Let 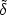_T(k) represent the true Fourier component of the underlying (noiseless) density field at wavevector k; the quantity with which we calculate the velocity field is the Wiener-filtered noisy image, whose Fourier modes are given by

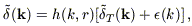
(B10)

where the Wiener filter itself is (e.g., Zaroubi et al. 1995)

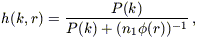
(B11)

and P(k) is set a priori; we used a functional fit to the IRAS power spectrum found by Fisher et al. (1993). The noise term in the denominator of the Wiener filter is independent of k (cf. Fisher et al. 1993; SW, Section 5.3); however, it is dependent on the density of galaxies, which is a decreasing function of distance in the flux-limited IRAS sample. As explained in Sigad et al. (1997), we therefore calculate a series of Wiener-filtered density fields for different noise levels and interpolate between them to find the appropriate density field at any given distance.

We wish to calculate the quadrupole due to the error in the derived density field, i.e., that due to the difference between equation (B10) and 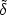_T(k). If we expand the density field in equation (B4) into its Fourier components, substitute this difference for each component, and square the result, we find the rms contribution to u_Q due to the Wiener filter:

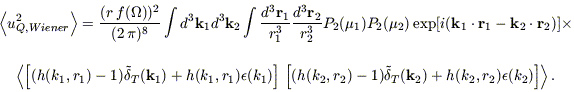
(B12)

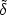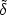This rather horrific expression can be simplified by multiplying out the term in braces, realizing that the cross terms vanish and that <_T(k₁) _T(k₂)> = (2)³ P_T(k) _D(k₁ - k₂), where P_T(k) is the true underlying power spectrum, not necessarily the same as that assumed in equation (B11). We then get two terms, one depending on the power spectrum and the other due to shot noise. For the first term, the integrals over r₁ and r₂ separate to give

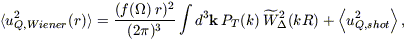
(B13)

where the new window function is given by

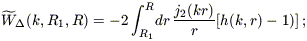
(B14)

(cf. eq. [B8]). We integrate from the outer volume of our peculiar velocity sample, R₁ = 3000 km s^-1, to R = 12,800 km s^-1; at smaller radii, the contribution to the quadrupole goes like r^-2, not r, and this is not included in our modeling of the quadrupole (eq. [19]). The contribution to the quadrupole from this term is between 1.5% and 3%, depending on which model we take for the true power spectrum. This is pleasingly close to the value we find for the real universe. The mock catalogs have a power spectrum set by the observed IRAS power spectrum (of course, with a cutoff at k < 2 /L) and thus give a somewhat smaller contribution to this integral, about 1%.

Let us now calculate the shot noise contribution to the quadrupole. It is given by

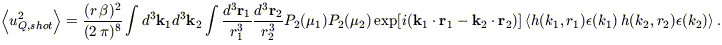
(B15)

Notice now the dependence on , not ; here we will make no reference to a COBE-normalized power spectrum. The Fourier modes are calculated in a box of side L = 25,600 km s^-1 and therefore are uncorrelated for k > 2 /L. Thus, we can write the product of the two shot noise terms as a Dirac delta function:

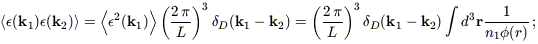
(B16)

the expression for <²(k)> comes from Fisher et al. (1993). When we insert equation (B16) into equation (B15), the latter simplifies dramatically. The integrals over r₁ and r₂ now separate, giving

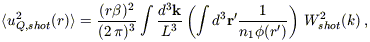
(B17)

where the shot noise window function looks very similar to what we have seen before:

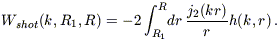
(B18)

Notice that unlike the previous calculation, this result is independent of the true power spectrum. If we calculate this using the observed IRAS selection function, integrating from 3000 to 12,800 km s^-1, we find an rms quadrupole of r^-1 <u²_{Q, shot}(r)>^1/2 = 1.7%.

We conclude that the 3.3% quadrupole found for the real data can be understood as a combination of the three effects discussed here: power on scales larger than the IRAS sample, the Wiener suppression factor, and shot noise; the Wiener suppression factor is the dominant one of the three. For the mock catalogs, we still do not understand completely why the measured residual quadrupole (< 1%) is smaller than we have calculated (~ 2%).