Annu. Rev. Astron. Astrophys. 1996. 34: 155-206 Copyright © 1996 by Annual Reviews. All rights reserved

2. INTERPRETATION OF RADIO OBSERVATIONS

Interstellar magnetic fields can be observed indirectly at optical and radio wavelengths. Heiles (1976), Verschuur (1979), Tinbergen (1996) provide extensive reviews of observational methods. In recent years, observations of the linearly polarized radio continuum emission have improved significantly; these provide the most extensive and reliable information about galactic magnetic fields. We thus concentrate on results based on radio continuum data. Zeeman splitting measurements are discussed by Heiles et al (1993). For optical and infrared polarization data, see Roberge & Whittet (1996).

2.1. Field Strength Estimates

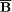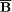
The strengths of the projections of the total (B) and regular () magnetic fields onto the plane of the sky (B and ) can be determined from the intensity of the total and linearly polarized synchrotron emission (e.g. Rybicki & Lightman 1979, p. 180). However, a relation between the energy densities of relativistic electrons, _e, and the total magnetic field, _B, has to be assumed. Direct measurements of cosmic rays are possible only near the Earth. The local cosmic-ray energy density _CR is comparable to _B, and K = _CR / _e 100 locally, but is possibly lower in other galaxies (Pohl 1993).

It is plausible to assume _CR = a_B, where a depends on the detailed model: pressure equilibrium, minimum total energy, or energy density equipartition. Although the validity of these assumptions may be questioned (Longair 1994, Urbanik et al 1994, Heiles 1996), they generally provide reasonable estimates.

Gamma-ray observations have been used to obtain indirect data about the distribution of cosmic-ray electrons in the Galaxy (Bloemen et al 1986) and in the Magellanic Clouds (Chi & Wolfendale 1993). Comparing radio and -ray data for the Magellanic Clouds, Chi & Wolfendale claimed that energy equipartition is not valid (see, however, Pohl 1993). Their arguments would not apply if and radio emissions originate from different regions.

The standard minimum-energy formulae generally use a fixed integration interval in frequency to determine the total energy density of cosmic-ray electrons. This procedure makes it difficult to compare minimum-energy field strengths between galaxies because a fixed frequency interval corresponds to different electron energy intervals, depending on the field strength itself. When a fixed integration interval in electron energy is used, the minimum-energy and energy equipartition estimates give similar values for <B² B^1+_s> <B^3+_s>, where _s is the synchrotron spectral index (typically 0.9). The resulting estimate <B^3+_s>^1/(3+_s) is larger than the mean field <B> if the field strength varies along the path length, since <B>^3+_s <B^3+_s>. (Here and elsewhere we denote the magnitude of a vector by B = |B|.)

If the field is concentrated in filaments with a volume filling factor f, the equipartition estimate is smaller than the field strength in the filaments by a factor f^1/(3+_s). The derived field strength depends on the power (3 + _s)^-1 1/4 of any of the input values, so that even large uncertainties cause only a moderate error in field strength. For example, a probable uncertainty in K of 50% gives an error in magnetic field strength of 15%, with the total uncertainty perhaps reaching 30%.

An estimate of the regular field strength can be obtained by using the observed degree of polarization P, from P P₀ ( / B)², where P₀ 75% (Burn 1966). Note that regular field strengths are always lower limits because of limited instrumental resolution.