


3.2. Constraints and Uncertainties
Time-delays can be predicted from lens modeling, for any observed image configuration and compared with the measured ones in order to infer the value of H0. The task requires detailed observations, deep, and at high angular resolution, and a good mass model for the lensing galaxy, as can be seen from the explicit expression for the time-delay in equations (1-3). A full description of the calculation can be found in Schneider, Ehlers & Falco (1992). We only use the result here to illustrate how observations help to achieve our goal. As explained above, the total time delay is the sum of two contributions, so that:
 |
(1) |
Each contribution to the total time-delay writes as:
 |
(2) |
 |
(3) |
where zL is the redshift of the lensing galaxy. As
illustrated in Fig. 3, the angle
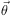 (in 2D in
real cases) gives the position of the images on the plane of the sky and
(in 2D in
real cases) gives the position of the images on the plane of the sky and
 is the
angular position of the source.
is the
angular position of the source.
The Hubble parameter H0 is contained in the geometrical part of the time-delay, through the angular diameter distances to the lens DL, to the source DS and through the distance between the lens and the source, DLS.
Equation (3), the gravitational part of the time-delay, depends only
on well known physical constants, and on the inverse of the 2D
Laplacian of the mass density profile in the lensing galaxy
 (
(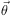 ). In other
words, it strongly depends on the shape of
the 2D mass profile of the lens (ellipticity, position angle), and on
its slope. We will see later that the main source of uncertainty on
the gravitational part of the time-delay comes from the radial
slope of the mass distribution.
). In other
words, it strongly depends on the shape of
the 2D mass profile of the lens (ellipticity, position angle), and on
its slope. We will see later that the main source of uncertainty on
the gravitational part of the time-delay comes from the radial
slope of the mass distribution.
Several of the ingredients necessary to compute the time-delay can be
precisely measured from observations. Although every lensed system has
its own particularities, the positions of the lensed images defined by
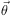 are
usually the easiest quantities to constrain. With
present day instrumentation, an accuracy of a few milli-arcsec is
reached. The position of the lensing galaxy relative to the quasar
images, when it is not double or multiple can be of the order of 10
milli-arcsec. As for the position
are
usually the easiest quantities to constrain. With
present day instrumentation, an accuracy of a few milli-arcsec is
reached. The position of the lensing galaxy relative to the quasar
images, when it is not double or multiple can be of the order of 10
milli-arcsec. As for the position
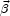 of the source relative to the lens, it is usually free in lens
models. No observation can constrain it.
of the source relative to the lens, it is usually free in lens
models. No observation can constrain it.
In most cases, astrometry is not a major limitation to the use of
lensed quasars. However, image configurations that are very symmetric
about the center of the lens are more sensitive to astrometric errors
than assymetric configurations. Let us assume that
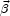 is very small compared with
is very small compared with
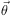 (i.e.,
the source is almost
aligned with the lens and the observer). Lets then consider a doubly
imaged quasar with two images located at positions
(i.e.,
the source is almost
aligned with the lens and the observer). Lets then consider a doubly
imaged quasar with two images located at positions
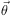 1
and
1
and
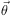 2
away from the lens, and separated by
2
away from the lens, and separated by
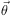 . The
geometrical time-delay between the two images is:
. The
geometrical time-delay between the two images is:
 |
(4) |
If we now consider that the error on the image separation
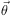 is much
smaller than the error on the position of image
1 relative to the lens,
is much
smaller than the error on the position of image
1 relative to the lens,
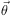 1,
we can approximate the error on the time-delay. Since the errors
d
1,
we can approximate the error on the time-delay. Since the errors
d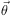 1 and
d
1 and
d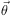 on
on
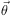 1
and
1
and
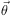 are not much
correlated, they propagate on the time-delay as
are not much
correlated, they propagate on the time-delay as
 |
(5) |
In symmetric configurations, where the lens is almost midway between
the images, 2|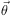 1|
1|
 |
|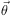 |, so
that the
denominator in equation (5) is zero or close to it, leading to large
relative errors on the time-delay, and hence on H0, whatever mass
model is adopted for the lensing galaxy.
|, so
that the
denominator in equation (5) is zero or close to it, leading to large
relative errors on the time-delay, and hence on H0, whatever mass
model is adopted for the lensing galaxy.
The advantage of symmetric configurations over assymetric ones is that they often have more than two lensed images (the source is more likely to be within the area enclosed by the radial caustic; see previous chapters on the basics of quasar lensing), offering the opportunity to measure several time-delays per system. The drawback is a larger sensitivity to astrometric errors.
Redshift information is also of capital importance in the calculation of the time-delay. Time-delays are proportional to (1 + zL) as seen in equation (4). The angular diameter distances also depend on the redshift of the lens and source zL and zS. Both should therefore be measured carefully. Although the lens and source redshifts are available for most know system, their measurement is not as straightforward as one could expect. Given the small separation between the lensed images and the high luminosity contrast between the source and lens, obtaining a spectrum of the lens is often challenging and may involve significant struggling with the data (e.g., Lidman et al. 2000). In other cases, for example in systems discovered in the radio, one faces the opposite situation: the optical counterpart of the source is so faint that no spectrum can be obtained of it, while the lens is well visible (e.g., Rusin et al. 2001).
Finally, the other cosmological parameters such as

 and
and  0
also play a role in the calculation of the time-delay,
through the angular diameter distances. The dependence of the
distances on (
0
also play a role in the calculation of the time-delay,
through the angular diameter distances. The dependence of the
distances on (
 ,
,
 0) is
however very weak. In
addition, other methods (Supernovae, CMB) seem much better at pinning
down their values than quasar lensing does. One shall therefore use
the known values of
(
0) is
however very weak. In
addition, other methods (Supernovae, CMB) seem much better at pinning
down their values than quasar lensing does. One shall therefore use
the known values of
(
 ,
,
 0) in
quasar lensing
and infer H0, to which it is much more sensitive.
0) in
quasar lensing
and infer H0, to which it is much more sensitive.