Annu. Rev. Astron. Astrophys. 1997. 35: 101-136 Copyright © 1997 by Annual Reviews. All rights reserved

8.3. Gould's Effect

Gould (1993) pointed out a complication present when a sample of galaxies to be used, for example, for infrared I-mag TF relation, is constructed from a sample originally based on selection criteria other than those of I mag, e.g. apparent diameter. 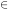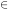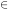The Malmquist bias of the first kind in the distance moduli from the I-mag TF relation does not now generally depend on the squared dispersion _I² = <_I²> of the I-mag TF relation nor on the squared dispersion _D² = <_D²> of the diameter relation, but on the covariance <_{I 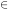D}> between the corresponding logarithmic distance errors 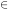. An interesting extreme case is when this covariance is zero, i.e. the deflections about the two TF relations are independent. Then there should be no Malmquist bias in the distance moduli from the I-mag TF relation. This is easy to understand: Though the original D-limited sample was selected "from the sky," the second set of I-mag measurements produces symmetrical residuals around the TF relation because of the assumed independence on D residuals and because in this case there is no I-mag limit (cf also Section 3.2 in Landy & Szalay 1992).

In practice, it may be difficult to find such pairs of observables that correlate with a common distance-independent parameter (e.g. TF parameter p), but have independent deflections (larger-than-average galaxies tend to be also more luminous than average). Also, it should be noted that the above argument is valid only if one could measure I for all the galaxies first taken from the D-limited sample, i.e. if the I limit was really = . In fact, though to measure the relevant covariance is one approach, Gould (1993) also sees the described problem as supporting the use of the "good old" B-band TF-relation. [For further discussions of Gould's effect, see Willick (1994), Strauss & Willick (1995).]

In the KLUN project (e.g. Paturel et al 1994), the sample of 5174 spirals has been selected on the basis of apparent size D₂₅ (in B), and in the analysis of the diameter TF distance moduli, Gould's effect should not appear. However, in such cases a somewhat related problem is that the measured diameters contain measurement error, and when one constructs a diameter-limited sample from measured galaxies, there is a Malmquist effect due to the dispersion in the measurement error: The sample contains an excess of overestimated apparent diameters. Ekholm & Teerikorpi (1997) pointed out that this may have a significant influence on the results, especially on those from the inverse TF relation where all galaxies (in view of the method's supposedly unbiased nature) are used. Assume now that the apparent sizes of such a diameter-limited sample are once more measured. Because the first and second measurement errors are independent, their influence vanishes from Gould's covariance, and now the second sample has correct measured apparent sizes, on the average. In practice, such a remeasurement of large samples is out of the question, and one has to be aware of the problem.