Copyright © 1982 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1982. 20:
399-429 Copyright © 1982 by Annual Reviews. All rights reserved |
4.2. Observations of Nonspherical Structure
PHOTOMETRY A number of authors have studied the shapes of the isophotes of elliptical galaxies during the last five years (King 1978, Carter 1979, Bertola & Galletta 1979, di Tullio 1979, Williams & Schwarzschild 1979, Leach 1981). The key points to have emerged from this work are the following.
1. The isophotes of ellipticals show little or no deviation from pure ellipses. This contrasts with the box-like shapes of the bulges of some lenticular galaxies.
2. The ellipticity
 (r) can vary
with semimajor axis length r in a complex
way. The isophotes generally do not tend to become circular near the center
as models that have distribution functions of the form
f = g(E) h(Jz) require,
though di Tullio (1979)
finds that this type of behavior is characteristic of the
brightest galaxies in clusters and groups. The isophotes of isolated
galaxies usually become more elliptical as the center is approached, and
every type of variation of
(r) can vary
with semimajor axis length r in a complex
way. The isophotes generally do not tend to become circular near the center
as models that have distribution functions of the form
f = g(E) h(Jz) require,
though di Tullio (1979)
finds that this type of behavior is characteristic of the
brightest galaxies in clusters and groups. The isophotes of isolated
galaxies usually become more elliptical as the center is approached, and
every type of variation of
 (r) occurs in
general group and cluster members.
(r) occurs in
general group and cluster members.
3. In some galaxies the major axes of different isophotes are not parallel to one another - that is, the isophotes are twisted. This phenomenon would not be possible if elliptical galaxies were axisymmetric and dust-free. It is readily understood if the isodensity surfaces of ellipticals are coaxial but triaxial ellipsoids, for then changes in the axial ratios of these ellipsoids would lead to the isophotes twisting on the sky (e.g. Mihalas & Binney 1981). Alternative explanations are that the isodensity surfaces are not coaxial, or that absorption by dust substantially alters the brightness profiles of these systems. Neither of these seems particularly attractive.
Statistical studies of the frequency with which elliptical galaxies of various apparent axial ratios occur have shown that the data may be accounted for very satisfactorily under any hypothesis as to the true shapes of elliptical galaxies: the galaxies may be oblate or prolate figures of revolution or any of the triaxial ellipsoids that lie between these extremes (Binney 1978a, Noerdlinger 1979, Binggelli 1980, Binney & de Vaucouleurs 1981). Under any hypothesis, the commonest ratio of the shortest to the longest body axes lies near 0.6:1. If most ellipticals are prolate, there must be more nearly spherical galaxies than if the oblate type is commonest.
If elliptical galaxies were identical prolate bodies, the central surface brightness of the best-fitting r1/4 profile of an apparently round galaxy would be higher than the corresponding quantity for an apparently highly elongated galaxy - and vice versa if galaxies were all oblate bodies. Attempts to detect such a correlation between surface brightness and apparent ellipticity (Marchant & Olson 1979, Richstone 1979) have tentatively concluded that the galaxies are more likely to be oblate than prolate. Lake (1979) has discussed the possibility that there is a similar correlation between ellipticity and central line-of-sight velocity dispersion. He concludes from a small data set that the galaxies studied may be prolate.
Galletta (1980) has confirmed that the most pronounced isophotal twists tend to occur in E1 and E0 galaxies. Only a small shift in the relative lengths of the body axes of successive isodensity surfaces in a nearly spherical galaxy is required to interchange the major and the minor axes and thus swing the apparent major axis through 90°.
The relative orientation of optical galaxies and any associated gas, dust, and radio components may lead to inferences about the shape of the optical galaxy (Bertola & Galletta 1978). Gas clouds are expected to settle quickly into closed orbits (Tohline et al. 1981). At most radii the only suitable closed orbits circulate about either the longest or shortest body axes of the potential (Heiligman & Schwarzschild 1979, Binney 1981); thus the plane of any dust or gas disk may be assumed to define one of these fundamental planes. Furthermore, observation suggests (Kotanyi & Ekers 1979) that radio jets tend to emerge along the rotation axes of these disks, just as one might expect if the radio sources are powered by accretion of the material of the disks onto compact objects. If radio axes are good tracers of the body axes of ellipticals, it is interesting that Battistini et al. (1980) find no evidence that radio axes align with the apparent principal axes of a sample of 51 galaxies, for this would indicate that these (abnormal) galaxies are strongly triaxial. Van Albada et al. (1981) have discussed the possibility of determining the angular velocity of the figures of radio galaxies from their radio structure.
SPECTROSCOPY The mean stellar rotation velocity has now been measured along the major axis of a few dozen elliptical galaxies out to radii r > 2 kpc at which the rotation curves cease to rise steeply. Some rotation is normally detected. By contrast, attempts to detect streaming motions along the apparent minor axes of normal galaxies have not yet produced unambiguous evidence, of minor-axis rotation (Williams 1979, Schechter & Gunn 1979). However, Jenkins & Scheuer (1980) find that two of three radio galaxies show minor-axis rotation.
The major-axis rotation curves are generally characterized by a steep rise just outside the center, followed by a long, flat or slightly falling portion. Exceptions to this pattern do occur, however. For example, Efstathiou et al. (1980) find that the rotation speed of the E1 galaxy NGC 5813 peaks 5" from the nucleus and then drops steeply to zero.
It is convenient to discuss the rotation of spheroidal components in
terms of the relationship between a characteristic ellipticity
 and the ratio
vp /
and the ratio
vp /
 of the
peak line-of-sight rotation speed vp to the central
velocity dispersion
of the
peak line-of-sight rotation speed vp to the central
velocity dispersion  .
Figure 1 plots the relationship between these
variables for elliptical galaxies. Evidently e is not correlated with
vp /
.
Figure 1 plots the relationship between these
variables for elliptical galaxies. Evidently e is not correlated with
vp /  .
.
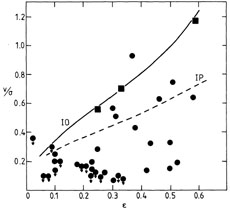 |
Figure 1. The ratio
vp / |
This result enables one to eliminate immediately the simplest picture of an elliptical galaxy - that in which the galaxy is an oblate spheroid in which the velocity dispersion is everywhere fairly isotropic and rotational-streaming is responsible for the galaxy's flattening [the isotropic oblate (IO) picture]. In fact, the flat rotation and velocity dispersion profiles of ellipticals imply that the projected central velocity dispersion should be nearly equal to the rms velocity dispersion through the entire galaxy; in addition, the projected peak rotation velocity in the IO picture should differ from the rms rotation velocity by a factor that depends in a simple way on the inclination angle i between the symmetry axis of the system and the line of sight. On the other hand, in this picture the apparent axial ratio of the galaxy also depends on the inclination i in a simple way, so that as i varies, the representative point of the galaxy in Figure 1 will move along a well-defined path. By good fortune, in the IO picture this path nearly coincides with the curve formed by the representative points, as estimated from the tensor virial theorem (Binney 1978a) of IO models that have i = 90° and various true flattenings. This curve is marked IO in Figure 1. If elliptical galaxies were rotationally flattened oblate figures of rotation, their representative points would lie close to these nearly coincident lines, rather than scattered all over the lower portion of the diagram.
It has been suggested that despite the wide scatter of the observational
points in Figure 1, the true shapes of
elliptical galaxies may be due to rotation, but
the rotation of prolate bodies that tumble end over end
(Miller & Smith 1980).
It is easy to understand that if elliptical galaxies were tumbling bars,
there could be no tight correlation between
 and
vp /
and
vp /  ;
when such a bar is viewed down its rotation axis it has large
;
when such a bar is viewed down its rotation axis it has large
 and small
vp /
and small
vp /  ,
and just the reverse when it is viewed down its long axis. In fact, the
representative points of a single
tumbling bar would occupy a more or less triangular region, two of whose
sides run parallel to the axes in
Figure 1, depending on the orientation
of the bar to the line of sight. Hence in this picture one would expect
the representative points of a number of galaxies to lie close to the
vp /
,
and just the reverse when it is viewed down its long axis. In fact, the
representative points of a single
tumbling bar would occupy a more or less triangular region, two of whose
sides run parallel to the axes in
Figure 1, depending on the orientation
of the bar to the line of sight. Hence in this picture one would expect
the representative points of a number of galaxies to lie close to the
vp /  axis in Figure 1
(where in fact there are no points). Furthermore, if one assumes that the
velocity dispersion in these bars is always isotropic, one may again
apply the virial theorem and the distribution of true ellipticities that
are required of such bars if the predicted distribution of apparent
ellipticities is to match the observed distribution, to predict the
expected distribution of points in Figure 1.
The line in the figure marked IP is such that half of the points should
lie above this line. Evidently elliptical galaxies cannot be prolate
bars having isotropic velocity distributions.
axis in Figure 1
(where in fact there are no points). Furthermore, if one assumes that the
velocity dispersion in these bars is always isotropic, one may again
apply the virial theorem and the distribution of true ellipticities that
are required of such bars if the predicted distribution of apparent
ellipticities is to match the observed distribution, to predict the
expected distribution of points in Figure 1.
The line in the figure marked IP is such that half of the points should
lie above this line. Evidently elliptical galaxies cannot be prolate
bars having isotropic velocity distributions.
Recent work on the bulges of early-type disk galaxies indicates that these
systems are quite unlike ellipticals, in that rotation probably accounts
for their flattenings.
Kormendy (1981a)
and Illingworth and co-workers
(Kormendy &
Illingworth 1982,
Illingworth &
Schechter 1981,
Verter et al., in preparation)
have mapped the velocity fields of a few normal lenticular and spiral
galaxies. When they extract from their observations the probable
rotation patterns of the
bulges of these systems, they find (a) the ratio of rotational to
random kinetic energy in these systems is nearly equal to that expected
in the IO picture (see
Figure 1); (b) the shapes of the
rotational curves of these galaxies
are similar to those of giant ellipticals; near the center
<v > rises steeply and then
becomes constant; and (c) most of these systems rotate as if they
were constructed of rigid coaxial spheroids, although one galaxy, NGC 4565,
which has a box-shaped bulge, rotates on cylinders.
> rises steeply and then
becomes constant; and (c) most of these systems rotate as if they
were constructed of rigid coaxial spheroids, although one galaxy, NGC 4565,
which has a box-shaped bulge, rotates on cylinders.
Kormendy (1981b) has studied the kinematics of six barred lenticulars. He finds that the bulges of these galaxies rotate at least as rapidly as the IO picture would suggest. Some of the bulges that appear to be triaxial rotate even faster than in the IO picture. This is to be expected if these bulges are tumbling bars that have near-isotropic velocity dispersion tensors.
Work undertaken by Davies et al. (in preparation) suggests that the differences between the rotation properties of giant ellipticals and those of the bulges of disk galaxies are related to differences in the luminosities of these two types of system; the absolute magnitudes of the bulges that contribute to Figure 1 lie in the range -18 > MB > -21, whereas the great majority of the elliptical galaxies contributing to this figure have MB < -20.5. Davies et al. find that all very-low-luminosity ellipticals rotate as rapidly as bulges of the same luminosity. Why this should be so is not clear.