Let us turn first to the issue of why the vacuum energy is smaller than we might expect. When Einstein proposed general relativity, his field equation was
 |
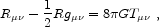(1.1) |
where the left-hand side characterizes the geometry of spacetime
and the right-hand side the energy sources;
gµ
is the
spacetime metric,
Rµ is
the Ricci tensor, R is the curvature scalar, and
Tµ is
the energy-momentum tensor. (I use conventions in which c =
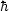= 1.) If the energy sources
are a combination of matter and radiation, there are no solutions
to (1.1) describing a static, homogeneous universe.
Since astronomers at the time believed the universe was static,
Einstein suggested modifying the left-hand side of his equation
to obtain
 |
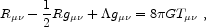(1.2) |
where 
is a new
free parameter, the cosmological
constant. This new equation admits a static, homogeneous solution
for which , the
matter density, and the spatial curvature
are all positive: the "Einstein static universe." The need for
such a universe was soon swept away by improved astronomical
observations, and the cosmological constant acquired a somewhat
compromised reputation.
Later, particle physicists began to contemplate the possibility of an energy density inherent in the vacuum (defined as the state of lowest attainable energy). If the vacuum is to look Lorentz-invariant to a local observer, its energy-momentum tensor must take on the unique form
 |
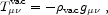(1.3) |
where
vac
is a constant vacuum energy density.
Such an energy is associated with an isotropic pressure
 |
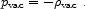(1.4) |
Comparing this kind of energy-momentum tensor to the appearance of the
cosmological constant in (1.2), we find that they
are formally equivalent, as can be seen by moving the
gµ term in
(1.2) to the right-hand side and setting
 |
(1.5) |
This equivalence is the origin of the identification of the cosmological constant with the energy of the vacuum.
From either side of Einstein's equation, the cosmological constant
is
a completely free parameter. It has dimensions of [length]-2
(while the energy density
has
units [energy/volume]), and hence defines a scale, while general
relativity is otherwise scale-free. Indeed, from purely classical
considerations, we can't even say whether a specific value of
is "large" or
"small"; it is simply a constant of nature we should go out and
determine through experiment.