2.4. Supersymmetric Dark Matter

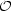The appearance of supersymmetry at the TeV scale was originally motivated by the hierarchy problem (Maiani 1979; 't Hooft 1979; Witten 1981) - why is m_W << m_P ~ 10¹⁹ GeV, the only candidate we have for a fundamental mass scale in physics, or alternatively why is the Coulomb potential in an atom so much larger than the Newton potential? The former is e² = (1), whereas the latter is G_N m² ~ m² / m_P², where m is a typical particle mass scale. It is not sufficient simply to set particle masses such as m_W >> m_P, since quantum corrections will increase them again. Many one-loop quantum corrections each yield

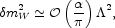(2.13)

where is an effective cut-off, representing the scale at which the Standard Model ceases to be valid, and new physics appears. If m_P or the GUT scale ~ 10¹⁶ GeV, the `small' correction (2.13) will be much larger than the physical value of m<sub>W</sub><sup>2</sup>. It would require `unnatural' fine-tuning to choose the bare value of m_W² to be almost equal and opposite to the `small' correction (2.13), so that their combination happens to have the right magnitude. Alternatively, supersymmetry introduces an effective cut-off by postulating equal numbers of bosons and fermions with identical couplings, in which case the corrections (2.13) cancel among themselves, leaving

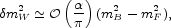(2.14)

which is m_W² if

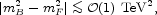(2.15)

i.e., if supersymmetry appears at relatively low energy.

This naturalness argument for low-energy supersymmetry is supported by several pieces of indirect empirical evidence. One is that the strengths of the different gauge interactions measured at low energies, particularly at the LEP accelerator, are consistent with unification at high energies if there are low-mass supersymmetric particles (Ellis et al. 1991b; Amaldi et al. 1991; Langacker & Luo 1991; Giunti et al. 1991). A second is that LEP and other precision low-energy data are fitted well by the Standard Model if there is a relatively light Higgs boson with mass < 200 GeV, very consistent with the range m_h 130 GeV predicted by supersymmetry (Okada et al. 1991; Ellis et al. 1991a; Haber & Hempfling 1991). A third is that the minimal supersymmetric extension of the Standard Model (MSSM) contains a good candidate for cold dark matter, which has a suitable relic density if the supersymmetric mass scale 1 TeV (Ellis et al. 1984; Goldberg 1983). A fourth may be provided by the anomalous magnetic moment of the muon, g_µ - 2 (Brown et al. 2001; Bennett et al. 2002), if its experimental value deviates significantly from the Standard Model prediction.

When considering the experimental, cosmological and theoretical constraints on the MSSM, it is common to assume that all the unseen spin-0 supersymmetric particles have some universal mass m₀ at some GUT input scale, and similarly for the unseen fermion masses m_1/2. These two parameters of this constrained MSSM (CMSSM) are restricted by the absences of supersymmetric particles at LEP: m^_± 103 GeV, m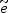 99 GeV, and at the Fermilab Tevatron collider. They are also restricted indirectly by the absence of a Higgs boson at LEP: m_h > 114.4 GeV, and by the fact that b s decay is consistent with the Standard Model, and potentially by the BNL measurement of g_µ - 2, as seen in Fig. 9 (Ellis et al. 2003a; Lahanas & Naopoulos 2003).

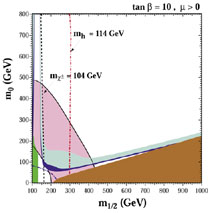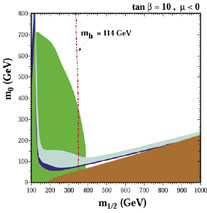Figure 9. The (m1/2, m0) planes for (left panel) tan = 10, µ > 0, and (right panel) tan = 10, µ < 0. In each panel, the region allowed by the older cosmological constraint 0.1 h2 0.3 has light shading, and the region allowed by the newer WMAP cosmological constraint 0.094 h2 0.129 has very dark shading. The region with dark (red) shading is disallowed because there the lightest supersymmetric particle would be charged. The regions excluded by b s have medium (green) shading, and those in panels (a,d) that are favoured by gµ - 2 at the 2- level have medium (pink) shading. LEP constraints on the Higgs and supersymmetric particle masses are also shown (Ellis et al. 2003a).

As shown there, the CMSSM parameter space is also restricted by cosmological bounds on the amount of cold dark matter, _CDM h². Since = m n, and the relic number density n 1 / _ann ( ...) where _ann ( ...) 1 / m², the relic density generically increases with increasing sparticle masses. For some time, the conservative upper limit on _CDM h² has been < 0.3 (Lahanas et al. 2000, 2001a, 2001b; Barger & Kao 2001; Arnowitt & Dutta 2002), but the recent WMAP data allow this to be reduced to < 0.129 at the 2- level. As seen in Fig. 9, this improved upper limit significantly improves the cosmological upper limit on the sparticle mass scale (Ellis et al. 2003a, Lahanas & Nanopoulos 2003). If there are other important components of the cold dark matter, the CMSSM parameters could lie below the dark (blue) strips in Fig. 9.

In order to facilitate discussion of the physics reaches of different accelerators and strategies for detecting dark matter, it is convenient to focus on a limited number of benchmark scenarios that illustrate the various different supersymmetric possibilities (Battaglia et al. 2001). In many of these scenarios, supersymmetry would be very easy to observe at the LHC, and many different types of supersymmetric particle might be discovered. However, searches for astrophysical dark matter may be competitive for some scenarios (Ellis et al. 2001).

One strategy is to look for relic annihilations out in the galactic halo, which might produce detectable antiprotons or positrons in the cosmic rays (Silk & Srednicki 1984). As discussed here by Carr (2003), both the PAMELA (Pearce et al. 2002) and AMS (Aguilar et al. 2002) space experiments will be looking for these signals, though the rates are not very promising in the benchmark scenarios we studied (Ellis et al. 2001). Alternatively, one might look for annihilations in the core of our galaxy, which might produce detectable gamma rays. As seen in the left panel of Fig. 10, this may be possible in certain benchmark scenarios (Ellis et al. 2001), although the rate is rather uncertain because of the unknown enhancement of relic particles in our galactic core. A third strategy is to look for annihilations inside the Sun or Earth (Silk et al. 1985), where the local density of relic particles is enhanced in a calculable way by scattering off matter, which causes them to lose energy and become gravitationally bound. The signature would then be energetic neutrinos that might produce detectable muons. As also discussed here by Carr (2003), several underwater and ice experiments are underway or planned to look for this signature, and this strategy looks promising for several benchmark scenarios, as seen in the right panel of Fig. 10 ¹.

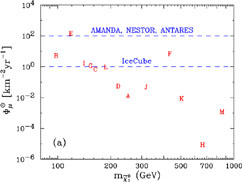Figure 10. Left panel: Spectra of photons from the annihilations of dark matter particles in the core of our galaxy, in different benchmark supersymmetric models (Ellis et al. 2001). Right panel: Signals for muons produced by energetic neutrinos originating from annihilations of dark matter particles in the core of the Sun, in the same benchmark supersymmetric models (Ellis et al. 2001).

The most satisfactory way to look for supersymmetric relic particles is directly via their scattering on nuclei in a low-background laboratory experiment Goodman & Witten 1985). There are two types of scattering matrix elements, spin-independent - which are normally dominant for heavier nuclei, and spin-dependent - which could be interesting for lighter elements such as fluorine. The best experimental sensitivities so far are for spin-independent scattering, and one experiment has claimed a positive signal (Bernabei et al. 1998). However, this has not been confirmed by a number of other experiments, as discussed here by Kraus (2003) and Smith (2003). In the benchmark scenarios the rates are considerably below the present experimental sensitivities, but there are prospects for improving the sensitivity into the interesting range, as also discussed by Kraus (2003) and Smith (2003), as seen in Fig. 11.

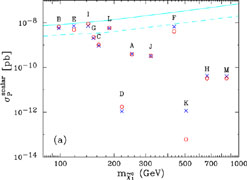Figure 11. Rates calculated for the spin-independent elastic scattering of dark matter particles off protons in the same benchmark supersymmetric models (Ellis et al. 2001) as in Fig. 10.

Overall, the searches for astrophysical supersymmetric dark matter have discovery prospects (Ellis et al. 2001) that are comparable with those of the LHC (Battaglia et al. 2001).

¹ It will be interesting to have such neutrino telescopes in different hemispheres, which will be able to scan different regions of the sky for astrophysical high-energy neutrino sources. Back.