3. CALCULATE IT!

Now that we have a good idea of the matter and energy content of the Universe, and some prospects for detecting it, the next task is to calculate it from first principles on the basis of microphysics and laboratory data.

_b: As Sakharov taught us (Sakharov 1967), baryogenesis requires the violation of charge conjugation C and its combination CP with parity, interactions that violate baryon number B, and a departure from thermal equilibrium. The first two have been observed for quarks, and are expected within the Standard Model. B violation is also expected in the Standard Model, at the non-perturbative level. One might therefore wonder whether the observed cosmological baryon asymmetry could have been generated by the Standard Model alone, but the answer seems to be no (Gavela et al. 1994). However, it might be possible in the MSSM, if it contains additional sources of CP violation beyond the Standard Model (Carena et al. 2003). An attractive alternative is leptogenesis (Fukugita & Yanagida 1986), according to which first the decays of heavy singlet neutrinos create a CP-violating asymmetry L 0, and then this is partially converted into a baryon asymmetry by non-perturbative weak interactions.

At the one-loop level, the asymmetry in the decays of one heavy singlet neutrino N_i due to exchanges of another one, N_j, is

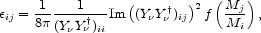(3.1)

where Y is a matrix of Yukawa couplings between heavy singlet and light doublet neutrinos. The expression (3.1) involves a sum over the light leptons, and hence is independent of the CP-violating MNS phase and the Majorana phases _1,2. Instead, it is controlled by extra phase parameters that are not directly accessible to low-energy experiments.

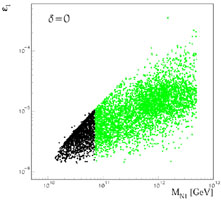
This leptogenesis scenario produces effortlessly a baryon-to-photon ratio Y_B of the right order of magnitude. However, as seen in Fig. 13, the CP-violating decay asymmetry (3.1) is explicitly independent of (Ellis & Raidal 2002). On the other hand, other observables such as the charged-lepton-flavour-violating decays µ e and µ may cast some indirect light on the mechanism of leptogenesis (Ellis et al. 2002a, b). Predictions for these decays may be refined if one makes extra hypotheses.

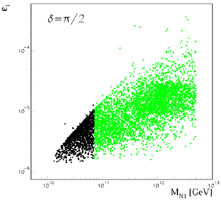Figure 13. Comparison of the CP-violating asymmetries in the decays of heavy singlet neutrinos giving rise to the cosmological baryon asymmetry via leptogenesis (left panel) without and (right panel) with maximal CP violation in neutrino oscillations (Ellis & Raidal 2002). They are indistinguishable.

One possibility is that the inflaton might be a heavy singlet sneutrino (Murayama et al. 1993, 1994). This would require a mass 2 × 10¹³ GeV, which is well within the range favoured by seesaw models. The sneutrino inflaton model predicts (Ellis et al. 2003b) values of the spectral index of scalar perturbations, the fraction of tensor perturbations and other CMB observables that are consistent with the WMAP data (Peiris et al. 2003). Moreover, this model predicts a branching ratio for µ e within a couple of orders of magnitude of the present experimental upper limit.

_CDM: The relic density of supersymmetric dark matter is calculable in terms of supersymmetric particle masses and Standard Model parameters. The sensitivity to these parameters is quite small in generic regions, but may be larger in some exceptional regions corresponding to `tails' of the MSSM parameter space (Ellis & Olive 2001). At least away from these regions, data from the LHC on supersymmetric parameters should enable the cold dark matter density to be calculated quite reliably.

: The biggest challenge may be the cosmological vacuum energy. For a long time, theorists tried to find reasons why the cosmological constant should vanish, but no convincing symmetry to guarantee this was ever found. Now cosmologists tell us that the vacuum energy actually does not vanish. Perhaps theorists' previous failure should be reinterpreted as a success? If the vacuum energy is indeed a constant, the hope is that it could be calculated from first principles in string or M theory. Alternatively, as argued here by Steinhardt 2003, perhaps the vacuum energy is presently relaxing towards zero, as in quintessence models (Maor et al. 2002). Such models are getting to be quite strongly constrained by the cosmological data, in particular those from high-redshift supernovae and WMAP (Spergel et al. 2003) as seen in Fig. 14, and it seems that the quintessence equation of state must be quite similar to that of a true cosmological constant (Spergel et al. 2003). Either way, the vacuum energy is a fascinating discovery that provides an exciting new opportunity for theoretical physics.

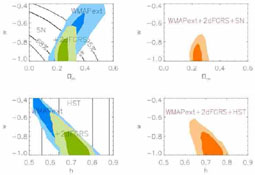Figure 14. Constraints on the equation of state of the dark energy from WMAP and other CMB data (WMAPext) combined with data on high-redshift supernovae, from the 2dF galaxy redshift survey and from the Hubble Space Telescope (Spergel et al. 2003).