2.2. Thermal Remnants

2.2.1. Cosmic Background Radiation

Entry 2.1 is based on the COBE measurement of the temperature of the thermal cosmic electromagnetic background radiation (the CMBR), T_o = 2.725 K (Mather et al. 1999). The COBE and UBC measurements (Mather et al. 1990; Gush, Halpern, & Wishnow 1990) show that the spectrum is very close to thermal. It has been slightly disturbed by the observed interaction with the hot plasma in clusters of galaxies (LaRoque et al. 2003 and references therein). The limit on the resulting fractional increase in the radiation energy density is (Fixsen et al. 1996)

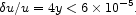(14)

This means that the background radiation energy density has been perturbed by the amount < 10^-8.5. Improvements of this number are under discussion (e.g. Zhang, Pen & Trac 2004), and might be entered in a future version of the inventory.

The thermal background radiation has been perturbed also by the dissipation of the primeval fluctuations in the distributions of baryons and radiation on scales smaller than the Hubble length at the epoch of decoupling of baryonic matter and radiation. If the initial mass fluctuations are adiabatic and scale-invariant the fractional perturbation to the radiation energy per logarithmic increment of the comoving length scale is u / u ~ _h², where _h ~ 10^-5 is the density contrast appearing at the Hubble length. This is small compared to the subsequent perturbation by hot plasma (eq [14]).

Entry 2.2 uses the standard estimates of the relict thermal neutrino temperature, T = (4/11)^1/3 T_o, and the number density per family, n = 112 cm^-3. We adopt the neutrino mass differences from oscillation experiments (Fukuda et al. 1998; Kameda et al. 2001; Eguchi, et al. 2003; Bahcall & Peña-Garay 2003),

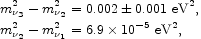(15)

where the neutrino mass eigenstates are ordered as m₁ < m₂ < m₃. Entry 2.2, the density parameter in primeval neutrinos, assumes that m_e may be neglected. The upper limit from WMAP and SDSS is < 0.04 (Tegmark et al. 2004a). At this limit the three families would have almost equal masses, m = 0.6 eV. This may not be very likely, but one certainly must bear in mind the possibility that our entry is a considerable underestimate.

2.2.2. Primordial Nucleosynthesis

Light elements are produced as the universe expanded and cooled through kT ~ 0.1 MeV, in amounts that depend on the baryon abundance. The general agreement of the baryon abundance inferred in this way with that derived from the CMBR temperature anisotropy gives confidence that the total amount of baryons - excluding what might have been trapped in the dark matter prior to light element nucleosynthesis - is securely constrained.

Estimates of the baryon density parameter from the WMAP and SDSS data (Spergel et al. 2003; Tegmark et al. 2004a), and from the deuterium (Kirkman et al. 2003) and helium abundance measurements (Izotov & Thuan 2004) are, respectively, _b h² = 0.023 ± 0.001, 0.0214 ± 0.0020, and 0.013^+.002_-0.001, where the last number is the all-sample average for helium from Izotov & Thuan. We adopt

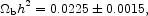(16)

close to the mean of the first two. Since the relation between the helium abundance and the baryon density parameter has a very shallow slope, an accurate abundance estimate (say, with < 1% error) is needed for a strong constraint on _b h². We consider that the current estimates may still suffer from systematic errors which are not included in the error estimates in the literature. ³ Within the standard cosmology our adopted value in equation (16) requires that the primeval helium abundance is

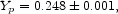(17)

and the ratio of the total matter density to the baryon component is

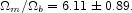(18)

We need in later sections the stellar helium production rate with respect to that of the heavy elements. The all-sample analysis of Izotov & Thuan (2004) gives Y / Z 2.8± 0.5. The value derived by Peimbert, Peimbert & Ruiz (2000) corresponds to 2.3± 0.6. These value may be compared to estimates from the perturbative effects on the effective temperature-luminosity relation for the atmosphere of main sequence dwarfs, Y / Z 3± 2 (Pagel & Portinari 1998), and 2.1± 0.4 (Jimenez et al. 2003). From the initial elemental abundance estimate in the standard solar model of Bahcall, Pinsonneault & Basu (2001; hereinafter BP2000) we derive Y / Z 1.4. We adopt

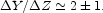(19)

Nuclear binding energy was released during nucleosynthesis. This appears in entry 2.3 as a negative value, meaning the comoving baryon mass density has been reduced and the energy density in radiation and neutrinos increased. The effect on the radiation background has long since been thermalized, of course, but the entry is worth recording for comparison to the nuclear binding energy released in stellar evolution. For the same reason, we compute the binding energy relative to free protons and electrons. The convention is artificial, because light element formation at high redshifts was dominated by radiative exchanges of neutrons, protons and atomic nuclei, and the abundance of the neutrons was determined by energy exchanges with the cosmic neutrino background. It facilitates comparison with category 6, however. The nuclear binding energy in entry 2.3 is the product

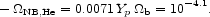(20)

This is larger in magnitude than the energy in the CMBR today.

³ We note, as an indication of the difficulty of these observations, that helium abundances inferred from the triplet 4d-2p transition (4471) are lower than what is indicated by the triplet 3d-2p (5876) and singlet 3d-2p (6678) transitions, by an amount that is significantly larger than the quoted errors. Another uncertainty arises from stellar absorption corrections, which are calculated only for the 4471 line. The table given in Izotov and Thuan suggests that a small change in absorption corrections for the 4471 line induces a sizable change in the final helium abundance estimate. We must remember also that Y / Z is not very well determined. Back.