2. TIME DELAY BASICS

The observations of gravitationally lensed quasars are best understood in light of Fermat's principle (e.g., Blandford & Narayan 1986). Intervening mass between a source and an observer introduces an effective index of refraction, thereby increasing the light-travel time. The competition between this Shapiro delay from the gravitational field and the geometric delay due to bending the ray paths leads to the formation of multiple images at the stationary points (minima, maxima, and saddle points) of the travel time (for more complete reviews, see Narayan & Bartelmann 1999 or Schneider, Ehlers, & Falco 1992).

As with glass optics, there is a thin-lens approximation that applies when the optics are small compared to the distances to the source and the observer. In this approximation, we need only the effective potential, () = (2 / c²)(D_ls / D_s) dz, found by integrating the 3D potential along the line of sight. The light-travel time is

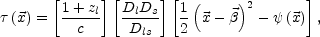(1)

where = (x, y) = R(cos , sin ) and are the angular positions of the image and the source, () is the effective potential, ( - )² / 2 is the geometric delay in the small-angle approximation, z_l is the lens redshift, and D_l, D_s, and D_ls are angular-diameter distances to the lens, to the source, and from the lens to the source, respectively. The only dimensioned quantity in the travel time is a factor of H₀^-1 10h^-1 Gyr arising from the H₀^-1 scaling of the angular-diameter distances.

We observe the images at the extrema of the time delay function, which we find by setting the gradients with respect to the image positions equal to zero, _x = 0, and finding all the stationary points (_A, _B, ...) associated with a given source position . The local magnification of an image is determined by the magnification tensor M_ij, whose inverse is determined by the second derivatives of the time delay function,

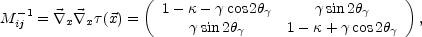(2)

where the convergence = / _c is the local surface density in units of the critical surface density _c = c² D_s / 4 G D_l D_ls, and and define the local shear field and its orientation. The determinant of the magnification tensor is the net magnification of the image, but it is a signed quantity depending on whether the image has positive (maxima, minima) or negative (saddle points) parity.

A simple but surprisingly realistic starting point for modeling lens potentials is the singular isothermal sphere (the SIS model) in which the lens potential is simply

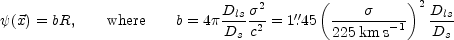(3)

is a deflection scale determined by geometry and is the 1D velocity dispersion of the lens galaxy. For || < b, the SIS lens produces two colinear images at radii R_A = || + b and R_B = b - || on opposite sides of the lens galaxy (as in Fig. 1 but with _AB = 180°). ⁽¹⁾ The A image is a minimum of the time delay and leads the saddle point, B, with a time delay difference of

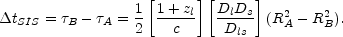(4)

Typical time delay differences of months or years are the consequence of multiplying the ~ 10h^-1 Gyr total propagation times by the square of a very small angle (b 3 × 10^-6 radians so, R_A² 10^-11). The SIS model suggests that lens time delay measurements reduce the determination of the Hubble constant to a problem of differential astrometry. This is almost correct, but we have made two idealizations in using the SIS model.

Figure 1. Schematic diagram of a two-image time delay lens. The lens lies at the origin, with two images A and B at radii RA and RB from the lens center. The images define an annulus of average radius <R> = (RA + RB) / 2 and width R = RA - RB, and the images subtend an angle AB relative to the lens center. For a circular lens AB = 180° by symmetry.

The first idealization was to ignore deviations of the radial (monopole) density profile from that of an SIS with density r^-2, surface density R^-1, and a flat rotation curve. The SIS is a special case of a power-law monopole with lens potential

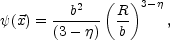(5)

corresponding to a (3D) density distribution with density r^-, surface density R^1-, and rotation curve _c r^{(2-) / 2}. For = 2 we recover the SIS model, and the normalization is chosen so that the scale b is always the Einstein ring radius. Models with smaller (larger) have less (more) centrally concentrated mass distributions and have rising (falling) rotation curves. The limit 3 approaches the potential of a point mass. By adjusting the scale b and the source position ||, we can fit the observed positions of two images at radii R_A and R_B on opposite sides ( _AB = 180°) of the lens for any value of . ⁽²⁾ The expression for the time delay difference can be well approximated by (Witt, Mao, & Keeton 2000; Kochanek 2002)

(6)

where <R> = (R_A + R_B) / 2 b and R = R_A - R_B (see Fig. 1). While the expansion assumes R / <R> (or ||) is small, we can usually ignore the higher-order terms. There are two important lessons from this model.

1. Image astrometry of simple two-image and four-image lenses generally cannot constrain the radial mass distribution of the lens.

2. More centrally concentrated mass distributions (larger ) predict longer time delays, resulting in a larger Hubble constant for a given time delay measurement.

These problems, which we will address from a different perspective in Section 3, are the cause of the uncertainties in estimates of H₀ from time delays.

The second idealization was to ignore deviations from circular symmetry due to either the ellipticity of the lens galaxy or the local tidal gravity field from nearby objects. A very nice analytic example of a lens with angular structure is a singular isothermal model with arbitrary angular structure, where the effective potential is = bRF(), and F() is an arbitrary function. The model family includes the most common lens model, the singular isothermal ellipsoid (SIE). The time delays for this model family are simply t_SIS, independent of the angular structure of the lens (Witt et al. 2000)! This result, while attractive, does not hold in general, and we will require the results of Section 3 to understand the effects of angular structure in the potential.

¹ The deflections produced by the SIS lens are constant, | - | = b, so the total image separation is always 2b. The outer image is brighter than the inner image, with signed magnifications M_A^-1 = 1 - b / R_A > 0 (a positive parity minimum) and M_B^-1 = 1 - b / R_B < 0 (a negative parity saddle point). The model parameters, b = (R_A + R_B) / 2 = <R> and || = (R_A - R_B) / 2 = R / 2, can be determined uniquely from the image positions. Back.

² In theory we have one additional constraint because the image flux ratio measures the magnification ratio, f_A / f_B = | M_A| / | M_B|, and the magnification ratio depends on . Unfortunately, the systematic errors created by milli- and microlensing make it difficult to use flux ratios as model constraints (see Section 5). Back.