


B.5.1. A General Theory of Time Delays
Just as for estimating mass distributions (Section B.4), the aspect of modeling time delays that creates the greatest suspicion is the need to model the gravitational potential of the lens. Just as for mass distributions, this problem is largely of our own making, arising from poor communication, understanding and competition between groups. Here we will use simple mathematical expansions to show exactly what properties of the potential determine time delays. Any models which have these generic properties have all the degrees of freedom needed to properly interpret time delays. This does not, unfortunately, avoid the problem of degeneracies between the mass models and the Hubble constant.
The key to understanding time delays comes from Gorenstein, Falco &
Shapiro
([1988],
Kochanek
[2002a],
see also Saha
[2000])
who showed that the time delay in a circular
lens depends only on the image positions and the surface density
 (
( ) in the annulus between the
images. The two lensed images at radii
) in the annulus between the
images. The two lensed images at radii
 A >
A >
 B define an
annulus bounded by their radii, with an interior region for
B define an
annulus bounded by their radii, with an interior region for
 <
<
 B and an
exterior region for
B and an
exterior region for  >
>
 A
(Fig. B.20). As we discussed in
Section B.4.1, the mass in the interior
region is implicit in
the image positions and constrained by the astrometry. From
Gauss' law we know that the distribution of the mass in the interior
and the amount or distribution of mass in the exterior region is
irrelevant (see Section B.4.3). A useful
approximation is to assume that the surface density
in the annulus can be locally approximated by a power law,
A
(Fig. B.20). As we discussed in
Section B.4.1, the mass in the interior
region is implicit in
the image positions and constrained by the astrometry. From
Gauss' law we know that the distribution of the mass in the interior
and the amount or distribution of mass in the exterior region is
irrelevant (see Section B.4.3). A useful
approximation is to assume that the surface density
in the annulus can be locally approximated by a power law,
 (
( )
)

 1-n for
1-n for
 B <
B <
 <
<
 A,
with a mean surface density in the annulus of
<
A,
with a mean surface density in the annulus of
< > =
<
> =
< > /
> /
 c.
The time delay between the images is then (Kochanek
[2002a])
c.
The time delay between the images is then (Kochanek
[2002a])
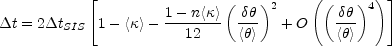 |
(B.97) |
where < > =
(
> =
( A +
A +
 B) / 2 and
B) / 2 and

 =
=
 A -
A -
 B as before.
Thus, the time delay is largely determined by the average surface density
<
B as before.
Thus, the time delay is largely determined by the average surface density
< > in the annulus
with only modest corrections from the local shape of the surface
density distribution even when
> in the annulus
with only modest corrections from the local shape of the surface
density distribution even when

 /
<
/
< > ~ 1. This
second order expansion is exact for an SIS lens
(<
> ~ 1. This
second order expansion is exact for an SIS lens
(< > = 1/2, n
= 2), and it reproduces the time delay of a point mass lens
(<
> = 1/2, n
= 2), and it reproduces the time delay of a point mass lens
(< > = 0) to better
than 1% even when
> = 0) to better
than 1% even when 
 /
<
/
< > = 1. The local
model also explains the scalings of the global power-law models. A
> = 1. The local
model also explains the scalings of the global power-law models. A


 1-n global power
law has surface density
<
1-n global power
law has surface density
< > = (3 -
n) / 2 near the Einstein ring, so the
leading term of the time delay is
> = (3 -
n) / 2 near the Einstein ring, so the
leading term of the time delay is
 t =
2
t =
2 SIS(1 -
<
SIS(1 -
< >) = (n -
1)
>) = (n -
1) tSIS
just as in Eqn. B.96.
tSIS
just as in Eqn. B.96.
The role of the angular structure of the lens is easily incorporated into
the expansion through the multipole expansion of
Section B.4. A
quadrupole term in the potential with dimensionless amplitude

 produces ray deflections of order
O(
produces ray deflections of order
O(
 b)
at the Einstein radius
b of the lens. In a four-image lens, the quadrupole deflections are
comparable to the fractional thickness of the annulus,
b)
at the Einstein radius
b of the lens. In a four-image lens, the quadrupole deflections are
comparable to the fractional thickness of the annulus,




 /
<
/
< >,
while in a two-image lens they are smaller. For an ellipsoidal density
distribution, the
cos(2m
>,
while in a two-image lens they are smaller. For an ellipsoidal density
distribution, the
cos(2m )
multipole amplitude is smaller than the quadrupole amplitude by
)
multipole amplitude is smaller than the quadrupole amplitude by
 2m ~
2m ~

 m
m
 (
(
 /
<
/
< >)m.
Hence, to lowest order in the expansion we only need to include the internal
and external quadrupoles of the potential but not the changes of the
quadrupoles in the annulus or any higher order multipoles. Remember that
what counts is the angular structure of the potential rather than of the
density, and that potentials are always much rounder than densities with
a typical scaling of m-2:m-1:1
between the potential, deflections and surface density for the
cos m
>)m.
Hence, to lowest order in the expansion we only need to include the internal
and external quadrupoles of the potential but not the changes of the
quadrupoles in the annulus or any higher order multipoles. Remember that
what counts is the angular structure of the potential rather than of the
density, and that potentials are always much rounder than densities with
a typical scaling of m-2:m-1:1
between the potential, deflections and surface density for the
cos m multipoles (see Section B.4.4)
multipoles (see Section B.4.4)
While the full expansion for independent internal and external quadrupoles
is too complex to be informative, the leading term for the case when the
internal and external quadrupoles are aligned is informative. We have
an internal shear of amplitude
 and an external
shear of amplitude
and an external
shear of amplitude
 with
with

 =
=

 as defined in
Eqns. B.51 and B.52. The leading term of the time delay is
as defined in
Eqns. B.51 and B.52. The leading term of the time delay is
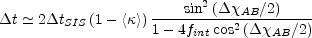 |
(B.98) |
where 
 AB is the angle
between the images (Fig. B.20)
and fint =
AB is the angle
between the images (Fig. B.20)
and fint =
 /
(
/
( +
+
 ) is the
internal quadrupole fraction we
explored in Fig. B.31.
We need not worry about a singular denominator - successful models of
the image positions do not allow such configurations.
) is the
internal quadrupole fraction we
explored in Fig. B.31.
We need not worry about a singular denominator - successful models of
the image positions do not allow such configurations.
A two-image lens has too few astrometric constraints to fully constrain
a model
with independent, misaligned internal and external quadrupoles. Fortunately,
when the lensed images lie on opposite sides of the lens galaxy
(
 AB
AB

 +
+
 with
|
with
| | << 1), the time
delay becomes insensitive to the quadrupole structure. Provided the
angular deflections are smaller than the radial deflections
(|
| << 1), the time
delay becomes insensitive to the quadrupole structure. Provided the
angular deflections are smaller than the radial deflections
(| |
<
|
< >
>


 ), the leading term of
the time delay reduces to the result for a circular lens,
), the leading term of
the time delay reduces to the result for a circular lens,
 t = 2
t = 2 tSIS(1
- <
tSIS(1
- < >)
if we minimize the total shear of the lens. In the minimum shear solution
the shear converges to the invariant shear
(
>)
if we minimize the total shear of the lens. In the minimum shear solution
the shear converges to the invariant shear
( 1)
and the other shear component
1)
and the other shear component
 2
= 0 (see Section B.4.5).
If, however, you allow the other shear
component to be non-zero, then you find that
2
= 0 (see Section B.4.5).
If, however, you allow the other shear
component to be non-zero, then you find that
 t =
2
t =
2 tSIS(1 - <
tSIS(1 - < > -
> -
 2)
to lowest order - the second shear component acts like a contribution to
the convergence. In the absence of any other constraints, this adds a modest
additional uncertainty (5-10%) to interpretations of time delays in
two-image lenses. To first order its effects should average out in an
ensemble of lenses because the extra shear has no preferred sign.
2)
to lowest order - the second shear component acts like a contribution to
the convergence. In the absence of any other constraints, this adds a modest
additional uncertainty (5-10%) to interpretations of time delays in
two-image lenses. To first order its effects should average out in an
ensemble of lenses because the extra shear has no preferred sign.
A four image lens has more astrometric constraints and can constrain a model
with independent, misaligned internal and external quadrupoles - this was
the basis of the Turner et al.
([2004])
summary of the internal to total quadrupole ratios shown in
Fig. B.31. If the external shear
dominates, then
fint  0 and the leading term of the delay becomes
0 and the leading term of the delay becomes
 t =
2
t =
2 tSIS(1 -
<
tSIS(1 -
< >)sin2
>)sin2

 AB / 2.
If the model is isothermal, like the
AB / 2.
If the model is isothermal, like the
 =
=
 F(
F( )
model we introduced in Eqn. B.42, then
fint = 1/4 and we obtain the Witt et al.
([2000])
result that the time delay is independent of the angle between the images
)
model we introduced in Eqn. B.42, then
fint = 1/4 and we obtain the Witt et al.
([2000])
result that the time delay is independent of the angle between the images
 t
t
 2
2 tSIS(1 -
<
tSIS(1 -
< >). Thus, delay
ratios in a four-image lens are largely determined by the angular
structure and provide a check on the potential model. Unfortunately, the
only lens with precisely measured delay ratios, B1608+656
(Fassnacht et al.
[2002]),
also has two galaxies inside
the Einstein ring and is a poor candidate for a simple multipole treatment
(although it is dominated by an internal quadrupole as expected, see
Fig. B.31).
The delay ratios for PG1115+080 are less well measured (Schechter et al.
[1997],
Barkana
[1997],
Chartas
[2003]),
but should be dominated by external shear since the estimate from the
image astrometry is that fint = 0.083 (0.055 <
fint < 0.111 at
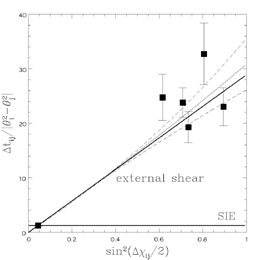
95% confidence). Fig. B.34 shows the
dependence of the
PG1115+080 delays on the leading angular dependence
of the time delay (Eqn. B.98) after scaling out the
standard astrometry factor for the different radii of the images
(Eqn. B.94). Formally, the estimate from the time delays
that fint = - 0.02 (-0.09 < fint
< 0.03 at 68% confidence) is
a little discrepant, but the two estimates agree at the 95% confidence
level and there are still some systematic uncertainties in the shorter
optical delays of PG1115+080. Changes in fint between
lenses is the reason Saha
([2004])
found significant scatter between time delays scaled only by
>). Thus, delay
ratios in a four-image lens are largely determined by the angular
structure and provide a check on the potential model. Unfortunately, the
only lens with precisely measured delay ratios, B1608+656
(Fassnacht et al.
[2002]),
also has two galaxies inside
the Einstein ring and is a poor candidate for a simple multipole treatment
(although it is dominated by an internal quadrupole as expected, see
Fig. B.31).
The delay ratios for PG1115+080 are less well measured (Schechter et al.
[1997],
Barkana
[1997],
Chartas
[2003]),
but should be dominated by external shear since the estimate from the
image astrometry is that fint = 0.083 (0.055 <
fint < 0.111 at
95% confidence). Fig. B.34 shows the
dependence of the
PG1115+080 delays on the leading angular dependence
of the time delay (Eqn. B.98) after scaling out the
standard astrometry factor for the different radii of the images
(Eqn. B.94). Formally, the estimate from the time delays
that fint = - 0.02 (-0.09 < fint
< 0.03 at 68% confidence) is
a little discrepant, but the two estimates agree at the 95% confidence
level and there are still some systematic uncertainties in the shorter
optical delays of PG1115+080. Changes in fint between
lenses is the reason Saha
([2004])
found significant scatter between time delays scaled only by
 tSIS, since the time delay lenses
range from external shear dominated systems like PG1115+080 to internal
shear dominated systems like B1608+656.
tSIS, since the time delay lenses
range from external shear dominated systems like PG1115+080 to internal
shear dominated systems like B1608+656.
 |
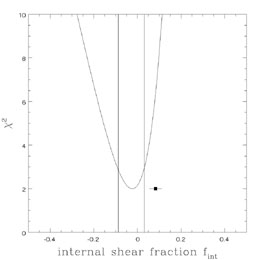 |
Figure B.34. (Top) The PG1115+080 time delays
scaled by the astrometric factor
|