B.8.1. Low Mass Dark Halos

When we are examining a particular lens, almost all the substructure will consist of satellites associated with the lens, with only a ~ 10% contamination from other small halos along the line-of-sight to the source (Chen, Kravtsov & Keeton [2003]). However, the excess of low mass halos in CDM mass functions relative to visible galaxies is a much more general problem because the low mass CDM satellites should exist everywhere, not just as satellites of massive galaxies. Crudely, luminosity functions diverge as dn / dL ~ 1 / L ~ 1 / M while CDM mass functions diverge as dn / dM ~ M^-1.8 so the fraction of low mass halos that must be dark increases ~ M^-0.8 at low masses. Fig. B.51 illustrates this assuming that all low mass halos have baryons which have cooled (e.g. Gonzalez et al. [2000], Kochanek [2003c]). In the context of CDM, the solution to this general problem is presumably the same as for the satellites responsible for anomalous flux ratio - they exist but lost their baryons before they could form stars. Such processes are implicit in semianalytic models which can reproduce galaxy luminosity function (e.g. Benson et al. [2003]) but can be modeled empirically in much the same way was employed for the break between galaxies in clusters in Section B.7 (e.g. Kochanek [2003c]). In any model, the probability of the baryons cooling to form a galaxy has to drop rapidly for halo masses below ~ 10¹¹ M just as it has to drop rapidly for halo masses above ~ 10¹³ M. Unlike groups and clusters, where we still expect to be able to detect the halos from either their member galaxies or X-ray emission from the hot baryons trapped in the halo, these low mass halos almost certainly cannot be detected in emission.

We can only detect isolated, low-mass dark halos if they multiply image background sources. For SIS lenses the distribution of image separations for small separations ( / _* << 1, Eqn. B.112) scales as

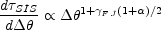(B.126)

where describes the divergence of the mass/luminosity function at low mass and _FJ is the conversion from mass to velocity dispersion (see Section B.6.2). For the standard parameters of galaxies, - 1 and _FJ 4, the separation distribution is d _SIS / d . In practice we do not observe this distribution because the surveys have angular selection effects that prevent the detection of small image separations (below 0."25 for the radio surveys), so the observed distributions show a much sharper cutoff (Fig. B.1). Even without a cutoff, there would be few lenses to find - the CLASS survey found 9 lenses between 0."3 1."0 in which case we expect only one lens with < 0."3 even in the absence of any angular selection effects. A VLBI survey of 3% of the CLASS sources with milli-arcsecond resolution found no lenses (Wilkinson et al. [2001]), nor would it be expected to for normal galaxy populations. Our non-parametric reconstruction of the velocity function including selection effects confirms that the existing lens samples are consistent with this standard model (Fig. B.50).

The result is very different if we extrapolate to low mass with the - 1.8 slope of the CDM halo mass function. The separation distribution becomes integrably divergent, d_SIS / d ^-0.6, and we would expect 15 lenses with < 0."3 given 9 between 0."3 1."0. Unfortunately, the Wilkinson et al. ([2001]) VLBI survey is too small to rule out such a model. A larger VLBI survey could easily do so, allowing the lenses to confirm the galaxy counting argument for the existence of second break in the density structure of halos at low mass (Kochanek [2003c], Ma [2003]) similar to the one between galaxies and high mass halos (Section B.7). If the baryons in the low mass halos either fail to cool, or cool and are then ejected by feedback, then their density distributions should revert to those of their CDM halos. If they are standard NFW halos, Ma ([2003]) shows that such low mass dark lenses will be very difficult to detect even in far larger surveys than are presently possible. Nonetheless, improving the scale of searches for very small separations from the initial attempt by Wilkinson et al. ([2001]) would provide valuable limits on their existence.

The resulting small, dark lenses would be the same as the dark lenses we discussed in Section B.7.2 for binary quasars and explored by Rusin ([2002]). They will also create the same problems about proving or disproving the lens hypothesis as was raised by the binary quasars with the added difficulty that they will be far more difficult to resolve. Time delays, while short enough to be easily measured, will also be on time scales where quasars show little variability. Confirmation of any small dark lens will probably requires systems with three or four images, rather than two images, and the presence of resolvable (VLBI) structures.