


1.4. The standard cosmological model
We now have most of the ingredients in place to describe the
cosmological model.
Beyond those of the previous subsections, there is only one parameter which
is essential, which is a measure of the ionization state of the
Universe. The Universe is known to be highly ionized at low redshifts
(otherwise radiation from
distant quasars would be heavily absorbed in the ultra-violet), and the
ionized
electrons can scatter microwave photons altering the pattern of observed
anisotropies. The most convenient parameter to describe this is the optical
depth to scattering  (i.e. the probability that a given photon
scatters once); in the approximation of instantaneous and complete
re-ionization, this could equivalently be described by the redshift of
re-ionization zion.
(i.e. the probability that a given photon
scatters once); in the approximation of instantaneous and complete
re-ionization, this could equivalently be described by the redshift of
re-ionization zion.
The basic set of cosmological parameters is therefore as shown in
Table 1.
The spatial curvature does not appear in the list, because it can be
determined from the other parameters using Eq. (1.1). The total
present matter density
 m =
m =
 dm +
dm +
 b is
usually used in place of the dark matter density.
b is
usually used in place of the dark matter density.
| Parameter | Symbol | Value |
| Hubble parameter | h | 0.73 ± 0.03 |
| Total matter density |
 m m |
 m
h2 = 0.134 ± 0.006 m
h2 = 0.134 ± 0.006 |
| Baryon density |
 b b |
 b
h2 = 0.023 ± 0.001 b
h2 = 0.023 ± 0.001 |
| Cosmological constant |   |
See Ref. [7] |
| Radiation density |
 r r |
 r
h2 = 2.47 × 10-5 r
h2 = 2.47 × 10-5 |
| Neutrino density |   |
See Sec. 1.2 |
| Density perturbation amplitude | 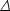 2 2 (k*) (k*) |
See Ref. [7] |
| Density perturbation spectral index | n | n = 0.97 ± 0.03 |
| Tensor to scalar ratio | r | r < 0.53 (95% conf) |
| Ionization optical depth |  |
 = 0.15 ± 0.07 = 0.15 ± 0.07 |
As described in Sec. 4, models based on these
ten parameters are
able to give a good fit to the complete set of high-quality data
available at present, and indeed some simplification is
possible. Observations are consistent
with spatial flatness, and indeed the inflation models so far described
automatically generate spatial flatness, so we can set k = 0; the
density parameters then must sum to
one, and so one can be eliminated. The neutrino energy density is often not
taken as an independent parameter. Provided the neutrino sector has the
standard
interactions the neutrino energy density while relativistic can be
related to the photon density
using thermal physics arguments, and it is currently difficult to see
the effect of the neutrino mass although observations of large-scale
structure have already placed interesting upper limits.
This reduces the standard parameter set to eight. In addition,
there is no observational evidence for the existence
of tensor perturbations (though the upper limits are quite weak), and so
r
could be set to zero. 1
More controversially, one could argue that as no
evidence against the Harrison-Zel'dovich spectrum has yet been seen,
then n could be set to one. We will however allow it to
vary. This leaves seven parameters, which is
the smallest set that can usefully be compared to the present
cosmological data set. This model is referred to by various names,
including  CDM, the
concordance cosmology, and the standard cosmological model.
CDM, the
concordance cosmology, and the standard cosmological model.
Of these parameters, only
 r is
accurately measured directly.
The radiation density is dominated by the energy in the cosmic microwave
background, and the COBE FIRAS experiment has determined its temperature
to be T = 2.725 ± 0.001 Kelvin
[8],
corresponding to
r is
accurately measured directly.
The radiation density is dominated by the energy in the cosmic microwave
background, and the COBE FIRAS experiment has determined its temperature
to be T = 2.725 ± 0.001 Kelvin
[8],
corresponding to
 r = 2.47
× 10-5 h-2.
r = 2.47
× 10-5 h-2.
In addition to this minimal set, there is a range of other parameters which might prove important in future as the dataset further improves, but for which there is so far no direct evidence, allowing them to be set to a specific value. We discuss various speculative options in the next section. For completeness at this point, we mention one other interesting parameter, the helium fraction, which is a non-zero parameter that can affect the microwave anisotropies at a subtle level. Presently, big-bang nucleosynthesis provides the best measurement of this parameter, and it is usually fixed in microwave anisotropy studies, but the data are just reaching a level where allowing its variation may become mandatory.
1 More controversially, one could argue that as no evidence against the Harrison-Zel'dovich spectrum has yet been seen, then n could be set to one. We will however allow it to vary. Back.