5.2. Carbon Star Kinematics

Among the discrete tracers in the LMC that have been studied kinematically, carbon stars have yielded some of the largest and most useful datasets in recent years. Van der Marel et al. (2002) fitted the general velocity field expression in equation (5.1) to the data for 1041 carbon stars, obtained from the work of Kunkel et al. (1997a) and Hardy, Schommer & Suntzeff (unpublished). The combined dataset samples both the inner and the outer parts of the LMC, although with a discontinuous distribution in radius and position angle. Figure 7 shows the data, with the best model fit overplotted. Overall, the model provides a good fit to the data.

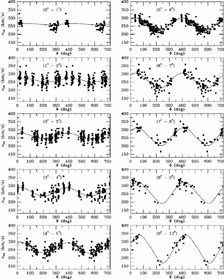Figure 7. Carbon star line-of-sight velocity data from Kunkel, Irwin & Demers (1997a) and Hardy et al. (unpublished), as function of position angle on the sky. The displayed range of the angle is 0°-720°, so each star is plotted twice. Each panel corresponds to a different range of angular distances from the LMC center, as indicated. The curves show the predictions of the best-fitting circularly-rotating disk model from van der Marel et al. (2002).

As discussed in Section 5.1, the line-of-nodes position angle is uniquely determined by the data; the model yields = 129.9° ± 6.0°. The LMC inclination cannot be determined kinematically, but it is known reasonably well from other considerations (see Section 6). With both viewing angles and the LMC proper motion known, the rotation curve V(R') follows from equation (5.3). The result is shown in Figure 8. The inferred rotation curve V(R') rises linearly in the central region and is roughly flat at V 50 km s^-1 for R' 4 kpc. The negative value at the innermost radius R' 0.5 kpc has limited significance; it is probably affected by the sparse coverage of the data at these radii (see Figure 7), as well as potential non-circular streaming motions in the region of the bar. The error bars on V(R') in Figure 8 reflect the random errors due to the sampling of the data. However, there are also contributions from the errors in the line-of-nodes position angle , the LMC proper motion and the inclination i. In particular, V(R') scales as 1 / sin i; and if the component v_tc of the transverse velocity vector along the line of nodes is larger than given in equation (4.1), then V(R') will go up. When all uncertainties are properly accounted for, the amplitude of the flat part of the rotation curve and its formal error become V = 49.8 ± 15.9 km s^-1.

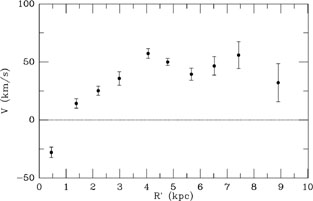Figure 8. Rotation velocity V of carbon stars in the plane of the LMC disk as function of the cylindrical radius R' in kpc from the carbon star fits of van der Marel et al. (2002). For reference, the exponential disk scale length of the LMC is approximately 1.4 kpc.

When asymmetric drift is corrected for, the circular velocity in the disk plane can be calculated to be V_circ = 64.8 ± 15.9 km s^-1. The implied total mass of the LMC inside the last measured data point is therefore M_LMC(8.9 kpc) = (8.7 ± 4.3) × 10⁹ M. By contrast, the total stellar mass of the LMC disk is ~ 2.7 × 10⁹ M and the mass of the neutral gas in the LMC is ~ 0.5 × 10⁹ M (Kim et al. 1998). The combined mass of the visible material in the LMC is therefore insufficient to explain the dynamically inferred mass. The LMC must therefore be embedded in a dark halo. This is consistent with the fact that the observed rotation curve amplitude is relatively flat as a function of radius. The LMC tidal radius can be calculated to be r_t = 15.0 ± 4.5 kpc, which corresponds to an angle on the sky of 17.1° ± 5.1°. The uncertainty in the tidal radius is due primarily to our ignorance of how far the LMC dark halo extends. Either way, the tidal radius extends beyond the region for which most observations of the main body of the LMC are available. However, it should be kept in mind that the tidal radius marks the position beyond which material becomes unbound. The structure of a galaxy can be altered well inside of this radius (Weinberg 2000).

As discussed in Section 5.1, the line-of-sight velocity field constrains the value of w_ts = v_ts + D₀(di / dt). The carbon stars yield w_ts = - 402.9 ± 13.0 km s^-1. Given our knowledge of the proper motion and distance of the LMC (see Section 4) this implies that di / dt = - 0.37 ± 0.22 mas yr^-1 = - 103 ± 61 degrees / Gyr. The LMC is the first galaxy for which it has been possible to measure di / dt. The N-body simulations by Weinberg (2000) show that the tidal torques from the Milky Way are expected to induce precession and nutation in the symmetry axis of the LMC disk plane. Although a detailed data-model comparison is not possible at the present time, it is comforting to note that the observed di / dt is of the same order as the rate of change of the disk orientation seen in the simulations.