B. Particle Acceleration

It is now generally accepted that Cosmic rays (more specifically the lower energy component below 10¹⁵ eV) are accelerated within shocks in SNRs is the Galaxy (see e.g. Gaisser [117]). A beautiful demonstration of this effect arises in the observation of synchrotron emission from Supernova remnants, which shows X-ray emission from these accelerated particles within the shocks.

The common model for particle shock acceleration is the Diffuse Shock Acceleration (DSA) model. According to this model the particles are accelerated when they repeatedly cross a shock. Magnetic field irregularities keep scattering the particles back so that they keep crossing the same shock. The competition [96] between the average energy gain, E_f / E_i per shock crossing cycle (upstream-downstream and back) and the escape probability per cycle, P_esc leads to a power-law spectrum N(E)dE E^-p dE with

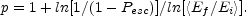(13)

Note that within the particle acceleration literature this index p is usually denoted as s. Our notation follows the common notation within the GRB literature.

Blandford and Eichler [29] review the theory of DSA in non-relativistic shocks. However, in GRBs the shocks are relativistic (mildly relativistic in internal shocks and extremely relativistic in external shocks). Acceleration in ultra relativistic shocks have been discussed by several groups [1, 17, 121, 161, 190, 424]. In relativistic shocks the considerations are quite different from those in non-relativistic ones. Using the relativistic shock jump conditions (Eq. 11 and kinematic considerations one can find (see Vietri [422], Gallant and Achterberg [122], Achterberg et al. [1]) that the energy gain in the first shock crossing is of the order _sh². However, subsequent shock crossing are not as efficient and the energy gain is of order unity <E_f / E_i> 2 [1, 122].

The deflection process in the upstream region is due to a large scale smooth background magnetic field perturbed by MHD fluctuations. A tiny change of the particle's momentum in the upstream region is sufficient for the shock to overtake the particle. Within the downstream region the momentum change should have a large angle before the particle overtakes the shock and reaches the upstream region. As the shock moves with a sub-relativistic velocity ( c / 3^1/2) relative to this frame it is easy for a relativistic particle to overtake the shock. A finite fraction of the particles reach the upstream region. Repeated cycles of this type (in each one the particles gain a factor of ~ 2 in energy) lead to a power-law spectrum with p 2.2 - 2.3 (for _sh >> 1). Like in non-relativistic shock this result it fairly robust and it does not depend on specific assumptions on the scattering process. It was obtained by several groups using different approaches, including both numerical simulations and analytic considerations. The insensitivity of this result arises, naturally from the logarithmic dependence in equation 13 and from the fact that both the denominator and the numerator are of order unity. This result agrees nicely with what was inferred from GRB spectrum [369] or with the afterglow spectrum [291]. Ostrowski and Bednarz [283] point out, however, that this result requires highly turbulent conditions downstream of the shock. If the turbulence is weaker the resulting energy spectrum could be much steeper. Additionally as internal shocks are only mildly relativistic the conditions in these shocks might be different.

The maximal energy that the shock accelerated particles can be obtained by comparing the age of the shock R / c (in the upstream frame) with the duration of an acceleration cycle. For a simple magnetic deflection, this later time is just half of the Larmour time, E / Z q_eB (in the same frame). The combination yields:

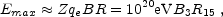(14)

where the values that I have used in the last equality reflect the conditions within the reverse external shocks where UHECRs (Ultra High Energy Cosmic Rays) can be accelerated (see Section VIIIC below). For particle diffusion in a random upstream field (with a diffusion length l) one finds that R in the above equation is replaced by (R l / 3)^1/2.

The acceleration process has to compete with radiation losses of the accelerated particles. Synchrotron losses are inevitable as they occur within the same magnetic field that is essential for deflecting the particles. Comparing the energy loss rate with the energy gain one obtain a maximal energy of:

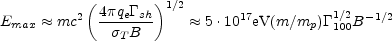(15)

The corresponding Lorentz factor is of the order of 10⁸ for _sh = 100 and B = 1 Gauss. Note that this formula assumes that the acceleration time is the Larmour time and hence that the synchrotron cooling time is equal to the Larmour time. Obviously it should be modified by a numerical factor which is mostly likely of order unity.