C. Light Curves for the early radiative phase

If the electrons' energy is large (namely if _e is not far from unity), then early on during the first few hours of the afterglow there will be a radiative phase in which a significant fraction of the kinetic energy is lost via the radiative processes. One can generalize the BM solution to this radiative stage (see Cohen et al. [58] and Section VIIA). The essence of the radiative phase is that in this case the energy varies as E , where (R / L)^-3. Note that L is calculated in terms of M and the initial energy of the explosion, E₀, via M = E₀ / ₀ c², where ₀ is the initial Lorentz factor of the ejecta:

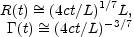(93)

The transition time from the radiative to the adiabatic phase takes place when the radiation losses become negligible. This happens at:

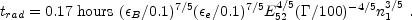(94)

Following Sari et al. [376] one can use the above expressions to express the different typical frequencies and fluxes as:

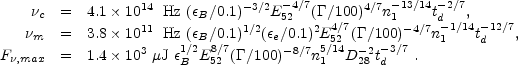(95)

Like in the adiabatic case this can be translated to the times of passage of the break frequencies at a given observed frequency:

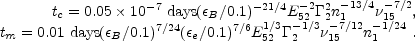(96)

Unlike the adiabatic case, here _c must be below _m. Otherwise the bulk of the electrons do not cool and the system won't be radiative. Indeed at t_rad (given by Eq. 94 above) _c = _m.