6.4. The Matter-Dominated Phase

The radiation dominated regime extends out to a radius r ~ (e₀ / ₀) r₀. At larger radii, the first and last terms in Eq. 20 become comparable and tends to its asymptotic value of _f = (4e₀ / 3₀ + 1)₀. This is the matter dominated regime. (The transition occurs when 4e / 3 = , which happens when = _f / 2.) In this regime, D r^2/3, leading to the scalings:

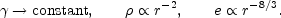(23)

The modified scalings of and e arise because the fireball now moves with a constant radial width in the comoving frame. (The steeper fall-off of e with r is because of the work done by the radiation through tangential expansion.) Moreover, since e << , the radiation has no important dynamical effect on the motion and produces no significant radial acceleration. Therefore, remains constant on streamlines and the fluid coasts with a constant asymptotic radial velocity. Of course, since each shell moves with a velocity that is slightly less than c and that is different from one shell to the next, the frozen pulse approximation on which Eq. 19 is based must ultimately break down at some large radius.