8.7. Shocks with the ISM - External shocks

We turn now to the interaction of a relativistic shell with the ISM. We have seen in section 7.4 that external shocks cannot produce bursts with a complicated temporal structure. Still it is worthwhile to explore this situation. First, there are some smooth bursts that might be produced in this way. Second, one needs to understand the evolution of external shocks in order to see why they cannot satisfy the condition R_E / ² . Third, it is possible that in some bursts emission is observed from both internal and external shocks [253]. Finally, as we see in the following section 9 the observed afterglow is most likely produced by external shocks.

8.7.1. Newtonian vs. Relativistic Reverse Shocks

The interaction between a relativistic flow and an external medium depends, like in SNRs, on the Sedov length, l (E / n_ism m_p c²)^1/3. The ISM rest mass energy within a volume l³ equals the energy of the GRB: E. For a canonical cosmological burst with E 10⁵² ergs and a typical ISM density n_ism = 1 particle/cm³ we have l 10¹⁸ cm. A second length scale that appears in the problem is , the width of the relativistic shell in the observer's rest frame.

There are two possible types of external shocks [233]. They are characterized according to the nature of the reverse shock: Newtonian Reverse Shock (NRS) vs. Relativistic Reverse Shock (RRS). If the reverse shock is relativistic (RRS) then it reduces significantly the kinetic energy of each layer that it crosses. Each layer within the shell loses its energy independently from the rest of the shock. The energy conversion process is over once the reverse shock crosses the shell (see Fig. 13). A Newtonian or even mildly relativistic reverse shock (NRS) is comparatively weak. Such a shock reduces the energy of the layer that it crosses by a relatively small amount. Significant energy conversion takes place only after the shock has crossed the shell several time after it has been reflected as a rarefraction wave from the inner edge (see Fig. 12). The shell behaves practically like a single object and it loses its energy only by the time that it accumulates an external mass equal to M / .

The question which scenario is taking place depends on the parameters of the shell relative to the parameters of the ISM. As we see shortly it depends on a single dimensionless parameter constructed from l, and : [233]:

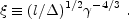(92)

As the shell propagates outwards it is initially very dense and the density ratio between the shell and the ISM, f n₄ / n₁, is extremely large (more specifically f > ²). The reverse shock is initially Newtonian (see Eq. 43). Such a shock converts only a small fraction of the kinetic energy to thermal energy. As the shell propagates the density ratio, f, decreases (like R^-2 if the width of the shell is constant and like R^-3 if the shell is spreading). Eventually the reverse shock becomes relativistic at R_N where f = ². The question where is the kinetic energy converted depends on whether the reverse shock reaches the inner edge of the shell before or after it becomes relativistic.

There are four different radii that should be considered. The following estimates assume a spherically symmetric shell, or that E and M are energy and rest mass divided by the fraction of a sphere into which they are launched. The reverse shock becomes relativistic at R_N, where f = n₄ / n₁ = 1:

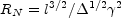(93)

Using the expression for the velocity of the reverse shock into the shell (Eq. 46) we find that the reverse shock reaches the inner edge of the shell at R [233]:

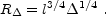(94)

A third radius is R, where the shell collects an ISM mass of M / [27, 18]. For NRS this is where an effective energy release occurs:

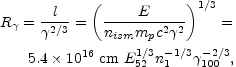(95)

where we defined n₁ = n_ism / 1 particle / cm³. Finally we have R = ², (see Eq. 73). The different radii are related by the dimensionless parameter , and this determines the character of the shock:

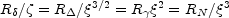(96)

If > 1 then:

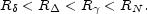(97)

The reverse shock remains Newtonian or at best mildly relativistic during the whole energy extraction process. The reverse shock reaches the inner edge of the shock at R while it is still Newtonian. At this stage a reflected rarefraction wave begins to move forwards. This wave is, in turn, reflected from the contact discontinuity, between the shell's material and the ISM material, and another reverse shock begins. The overall outcome of these waves is that in this case the shell acts as a single fluid element of mass M E / c² that is interacting collectively with the ISM. It follows from Eq. 39 that an external mass m = M / is required to reduce to / 2 and to convert half of the kinetic energy to thermal energy. Energy conversion takes place at R. Comparison of R with R_e (equation 27) shows that the optical depth is much smaller than unity.

If the shell propagates with a constant width then R_N / = R = ^1/2 R (see Fig. 25) and for > 1 the reverse shock remains Newtonian during the energy extraction period. If there are significant variations in the particles velocity within the shell it will spread during the expansion. If the typical variation in is of the same order as then the shell width increases like R / ². Thus changes with time in such a manner that at each moment the current width, (t), satisfies (t) ~ max[(0), R / ²]. This delays the time that the reverse shock reaches the inner edge of the shell and increases R. It also reduces the shell's density which, in turn, reduces f and leads to a decrease in R_N. The overall result is a triple coincidence R_N R R with a mildly relativistic reverse shock and a significant energy conversion in the reverse shock as well. This means that due to spreading a shell which begins with a value of > 1 adjusts itself so as to satisfy = 1.

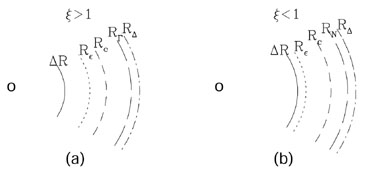Figure 25. (a) Schematic description of the different radii for the case > 1. The different distances are marked on a logarithmic scale. Beginning from the inside we have R, the initial size of the shell, R, the radius in which a fireball becomes matter-dominated (see the following discussion), Rc, the radius where inner shells overtake each other and collide, R, where the reverse shock reaches the inner boundary of the shell, and R, where the kinetic energy of the shell is converted into thermal energy. (b) Same as (a) for < 1. R does not appear here since it is not relevant. RN marks the place where the reverse shock becomes relativistic. From [31]

For 1 we find that T_radial ~ T_ang ~ R / ² > . Therefore, NRS can produce only smooth bursts. The bursts' duration is determined by the slowing down time of the shell. In section 7 we have shown that only one time scale is possible in this case. Given the typical radius of energy conversion, R this time scale is:

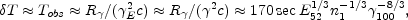(98)

If or are larger then < 1. In this case the order is reversed:

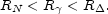(99)

The reverse shock becomes relativistic very early (see Fig. 25). Since _sh = ₂ << the relativistic reverse shock converts very efficiently the kinetic energy of the shell to thermal energy. Each layer of the shell that is shocked loses effectively all its kinetic energy at once and the time scale of converting the shell's kinetic energy to thermal energy is the shell crossing time. The kinetic energy is consumed at R, where the reverse shock reaches the inner edge of the shell. Using Eq. 94 for R and Eq. 45 we find that at R

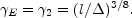(100)

Note that _E is independent of . The observed radial or angular time scales are:

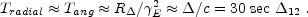(101)

Thus even for RRS we find that T ~ T and there is only one time scale. This time scale depends only on and it is independent of ! Spreading does not affect this estimate since for < 1 spreading does not occur before the energy extraction.

In the following discussions we focus on the RRS case and we express all results in terms of the parameter . By setting < 1 in the expressions we obtain results corresponding to RRS, and by choosing = 1 in the same expressions we obtain the spreading NRS limit. We shall not discuss the case of non-spreading NRS ( >> 1), since spreading will always bring these shells to the mildly relativistic limit ( ~ 1). Therefore, in this way, the same formulae are valid for both the RRS and NRS limits.

If > 1 it follows from Eq. 97 that internal shocks will take place before external shocks. If < 1 then the condition for internal shocks R < R becomes Eq. 74: ^3/2 > . As we have seen earlier (see section 8.6.1) this sets an upper limit on for internal shocks.

8.7.2. Physical Conditions in External Shocks

The interaction between the outward moving shell and the ISM takes place in the form of two shocks: a forward shock that propagates into the ISM and a reverse shock that propagates into the relativistic shell. This results in four distinct regions: the ISM at rest (denoted by the subscript 1 when we consider properties in this region), the shocked ISM material which has passed through the forward shock (subscript 2 or f), the shocked shell material which has passed through the reverse shock (3 or r), and the unshocked material in the shell (4). See Fig. 21. The nature of the emitted radiation and the efficiency of the cooling processes depend on the conditions in the shocked regions 2 and 3. Both regions have the same energy density e. The particle densities n₂ and n₃ are, however, different and hence the effective "temperatures," i.e. the mean Lorentz factors of the random motions of the shocked protons and electrons, are different.

The bulk of the kinetic energy of the shell is converted to thermal energy via the two shocks at around the time the shell has expanded to the radius R. At this radius, the conditions at the forward shock are as follows,

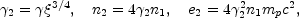(102)

while at the reverse shock we have

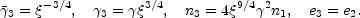(103)

Substitution of _sh = ₂ = ^3/4 in Eq. 49 yields:

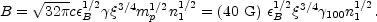(104)

If the magnetic field in region 2 behind the forward shock is obtained purely by shock compression of the ISM field, the field would be very weak, with _B << 1. Such low fields are incompatible with observations of GRBs. We therefore consider the possibility that there may be some kind of a turbulent instability which may bring the magnetic field to approximate equipartition. In the case of the reverse shock, magnetic fields of considerable strength might be present in the pre-shock shell material if the original exploding fireball was magnetic. The exact nature of magnetic field evolution during fireball expansion depends on several assumptions. Thompson [224] found that the magnetic field will remain in equipartition if it started off originally in equipartition. Mészáros, Laguna & Rees [240] on the other hand estimated that if the magnetic field was initially in equipartition then it would be below equipartition by a factor of 10^-5 by the time the shell expands to R. It is uncertain which, if either, is right. As in the forward shock, an instability could boost the field back to equipartition. Thus, while both shocks may have _B << 1 with pure flux freezing, both could achieve _B 1 in the presence of instabilities. In principle, _B could be different for the two shocks, but we limit ourselves to the same _B in both shocks.

In both regions 2 and 3 the electrons have a power law distribution with a minimal Lorentz factor _e,min given by Eq. 53 with the corresponding Lorentz factors for the forward and the reverse shock.

8.7.3. Synchrotron Cooling in External Shocks

The typical energy of synchrotron photons as well as the synchrotron cooling time depend on the Lorentz factor _e of the relativistic electrons under consideration and on the strength of the magnetic field. Using Eq. 53 for _e,min we find the characteristic synchrotron energy for the forward shock:

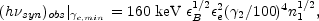(105)

and

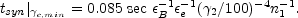(106)

The characteristic frequency and the corresponding cooling time for the "typical" electron are larger by a factor of [(p - 2) / (p - 1)]² and shorter by a factor of [(p - 2) / (p - 1)]², correspondingly.

These photons seems to be right in the observed soft gamma-ray range. However, one should recall that the frequency calculated in Eq. 105 depends on the forth power of ₂. An increase of the canonical ₂ by a factor of 3(that is ₂ = 300 instead of ₂ = 100) will yield a "typical" synchrotron emission at the 16 MeV instead of 160 keV. The Lorentz factor of a "typical electron" in the reverse shock is lower by a factor ^3/2. Therefore the observed energy is lower by a factor ³ while the cooling time scale is longer by a factor ^-3/4.

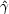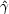Alternatively we can check the conditions in order that there are electrons with a Lorentz factor _e that be emitting soft gamma-rays with energies ~ 100 keV. Using Eq. 56 we calculate _e:

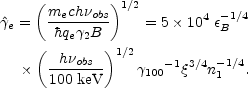(107)

Electrons with _e = 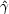_e are available in the shocked material if _e,min < 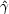_e. This corresponds to the condition

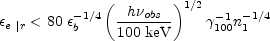(108)

in the reverse shock, and the condition

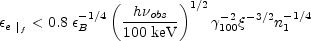(109)

in the forward shock. Since by definition _e 1, we see that the reverse shock always has electrons with the right Lorentz factors to produce soft gamma-ray synchrotron photons. However, the situation is marginal in the case of the forward shock. If > 100 and if the heating of the electrons is efficient, i.e. if _e |f ~ 1, then most of the electrons may be too energetic. Of course, as an electron cools, it radiates at progressively softer energies. Therefore, even if _min is initially too large for the synchrotron radiation to be in soft gamma-rays, the same electrons would at a later time have _e ~ 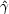_e and become visible. However, the energy remaining in the electrons at the later time will also be lower (by a factor 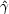/ _min), which means that the burst will be inefficient. For simplicity, we ignore this radiation.

Substituting the value of 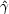_e from equation 107 into the cooling rate Eq. 58 we obtain the cooling time scale as a function of the observed photon energy to be

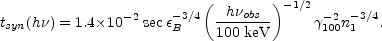(110)

Eq. 110 is valid for both the forward and reverse shock, and is moreover independent of whether the reverse shock is relativistic or Newtonian.

The cooling time calculated above sets a lower limit to the variability time scale of a GRB since the burst cannot possibly contain spikes that are shorter than its cooling time. However, it is unlikely that this cooling time actually determines the observed time scales.