2.4. Nonstandard BBN

The predictions of the primordial abundance of ⁴He depend sensitively on the early expansion rate (the Hubble parameter H) and on the amount - if any - of a _e - _e asymmetry (the _e chemical potential µ_e or the neutrino degeneracy parameter _e). In contrast to ⁴He, the BBN-predicted abundances of D, ³He and ⁷Li are determined by the competition between the various two-body production/destruction rates and the universal expansion rate. As a result, the D, ³He, and ⁷Li abundances are sensitive to the post-e^± annihilation expansion rate, while that of ⁴He depends on both the pre- and post-e^± annihilation expansion rates; the former determines the "freeze-in" and the latter modulates the importance of -decay (see, e.g., Kneller & Steigman 2003). Also, the primordial abundances of D, ³He, and ⁷Li, while not entirely insensitive to neutrino degeneracy, are much less affected by a nonzero _e (e.g., Kang & Steigman 1992). Each of these nonstandard cases will be considered below. Note that the abundances of at least two different relic nuclei are needed to break the degeneracy between the baryon density and a possible nonstandard expansion rate resulting from new physics or cosmology, and/or a neutrino asymmetry.

2.4.1. Additional Relativistic Energy Density

The most straightforward variation of SBBN is to consider the effect of a nonstandard expansion rate H' H. To quantify the deviation from the standard model it is convenient to introduce the "expansion rate factor" (or speedup/slowdown factor) S, where

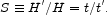(7)

Such a nonstandard expansion rate might result from the presence of "extra" energy contributed by new, light (relativistic at BBN) particles "X". These might, but need not, be additional flavors of active or sterile neutrinos. For X particles that are decoupled, in the sense that they do not share in the energy released by e^± annihilation, it is convenient to account for the extra contribution to the standard-model energy density by normalizing it to that of an "equivalent" neutrino flavor (Steigman et al. 1977),

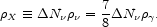(8)

For SBBN, N = 0 (N 3 + N) and for each such additional "neutrino-like" particle (i.e. any two-component fermion), if T_X = T, then N = 1; if X should be a scalar, N = 4/7. However, it may well be that the X have decoupled even earlier in the evolution of the Universe and have failed to profit from the heating when various other particle-antiparticle pairs annihilated (or unstable particles decayed). In this case, the contribution to N from each such particle will be < 1 (< 4/7). Henceforth we drop the X subscript. Note that, in principle, we are considering any term in the energy density that scales like "radiation" (i.e. decreases with the expansion of the Universe as the fourth power of the scale factor). In this sense, the modification to the usual Friedman equation due to higher dimensional effects, as in the Randall-Sundrum model (Randall & Sundrum 1999a, b; see also Cline, Grojean, & Servant 1999; Binetruy et al. 2000; Bratt et al. 2002), may be included as well. The interest in this latter case is that it permits the possibility of an apparent negative contribution to the radiation density ( N < 0; S < 1). For such a modification to the energy density, the pre-e^± annihilation energy density in Equation 1 is changed to

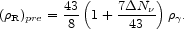(9)

Since any extra energy density ( N > 0) speeds up the expansion of the Universe (S > 1), the right-hand side of the time-temperature relation in Equation 3 is smaller by the square root of the factor in parentheses in Equation 9.

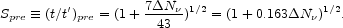(10)

In the post-e^± annihilation Universe the extra energy density is diluted by the heating of the photons, so that

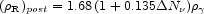(11)

and

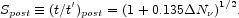(12)

While the abundances of D, ³He, and ⁷Li are most sensitive to the baryon density (), the ⁴He mass fraction (Y) provides the best probe of the expansion rate. This is illustrated in Figure 2 where, in the N - ₁₀ plane, are shown isoabundance contours for D/H and Y_P (the isoabundance curves for ³He/H and for ⁷Li/H, omitted for clarity, are similar in behavior to that of D/H). The trends illustrated in Figure 2 are easy to understand in the context of the discussion above. The higher the baryon density (₁₀), the faster primordial D is destroyed, so the relic abundance of D is anticorrelated with ₁₀. But, the faster the Universe expands ( N > 0), the less time is available for D destruction, so D/H is positively, albeit weakly, correlated with N. In contrast to D (and to ³He and ⁷Li), since the incorporation of all available neutrons into ⁴He is not limited by the nuclear reaction rates, the ⁴He mass fraction is relatively insensitive to the baryon density, but it is very sensitive to both the pre- and post-e^± annihilation expansion rates (which control the neutron-to-proton ratio). The faster the Universe expands, the more neutrons are available for ⁴He. The very slow increase of Y_P with ₁₀ is a reflection of the fact that for a higher baryon density, BBN begins earlier, when there are more neutrons. As a result of these complementary correlations, the pair of primordial abundances y_D 10⁵(D / H)_P and Y_P, the ⁴He mass fraction, provide observational constraints on both the baryon density () and on the universal expansion rate factor S (or on N) when the Universe was some 20 minutes old. Comparing these to similar constraints from when the Universe was some 380 Kyr old, provided by the WMAP observations of the CBR polarization and the spectrum of temperature fluctuations, provides a test of the consistency of the standard models of cosmology and of particle physics and further constrains the allowed range of the present-Universe baryon density (e.g., Barger et al. 2003a, b; Crotty, Lesgourgues, & Pastor 2003; Hannestad 2003; Pierpaoli 2003).

Figure 2. Isoabundance curves for D and 4He in the N - 10 plane. The solid curves are for 4He (from top to bottom: Y = 0.25, 0.24, 0.23). The dotted curves are for D (from left to right: yD 105(D/H) = 3.0, 2.5, 2.0). The data point with error bars corresponds to yD = 2.6 ± 0.4 and YP = 0.238 ± 0.005; see the text for discussion of these abundances.

2.4.2. Neutrino Degeneracy

The baryon-to-photon ratio provides a dimensionless measure of the universal baryon asymmetry, which is very small ( 10^-9). By charge neutrality the asymmetry in the charged leptons must also be of this order. However, there are no observational constraints, save those to be discussed here (see Kang & Steigman 1992; Kneller et al. 2001, and further references therein), on the magnitude of any asymmetry among the neutral leptons (neutrinos). A relatively small asymmetry between electron type neutrinos and antineutrinos (_e 10^-2) can have a significant impact on the early-Universe ratio of neutrons to protons, thereby affecting the yields of the light nuclides formed during BBN. The strongest effect is on the BBN ⁴He abundance, which is neutron limited. For _e > 0, there is an excess of neutrinos (_e) over antineutrinos (_e), and the two-body reactions regulating the neutron-to-proton ratio (Eq. 5) drive down the neutron abundance; the reverse is true for _e < 0. The effect of a nonzero _e asymmetry on the relic abundances of the other light nuclides is much weaker. This is illustrated in Figure 3, which shows the D and ⁴He isoabundance curves in the _e - ₁₀ plane. The nearly horizontal ⁴He curves reflect the weak dependence of Y_P on the baryon density, along with its significant dependence on the neutrino asymmetry. In contrast, the nearly vertical D curves reveal the strong dependence of y_D on the baryon density and its weak dependence on any neutrino asymmetry (³He/H and ⁷Li/H behave similarly: strongly dependent on , weakly dependent on _e). This complementarity between y_D and Y_P permits the pair {, _e} to be determined once the primordial abundances of D and ⁴He are inferred from the appropriate observational data.

Figure 3. Isoabundance curves for D and 4He in the e - 10 plane. The solid curves are for 4He (from top to bottom: YP = 0.23, 0.24, 0.25). The dotted curves are for D (from left to right: yD 105(D/H) = 3.0, 2.5, 2.0.) The data point with error bars corresponds to yD = 2.6 ± 0.4 and YP = 0.238 ± 0.005; see the text for discussion of these abundances.