2.1. Early-Universe Expansion Rate

The Friedman equation relates the expansion rate (measured by the Hubble parameter H) to the energy density (): H² = (8 G / 3) where, during the early, "radiation-dominated" (RD) evolution the energy density is dominated by the relativistic particles present ( = _R). For SBBN, prior to e^± annihilation, these are: photons, e^± pairs and, three flavors of left-handed (i.e. one helicity state) neutrinos (and their right-handed, antineutrinos).

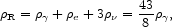(2)

where is the energy density in CBR photons. At this early epoch, when T few MeV, the neutrinos are beginning to decouple from the - e^± plasma and the neutron to proton ratio, crucial for the production of primordial ⁴He, is decreasing. The time-temperature relation follows from the Friedman equation and the temperature dependence of

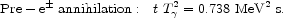(3)

To a very good (but not exact) approximation the neutrinos (_e, _µ, ) are decoupled when the e^± pairs annihilate as the Universe cools below m_e c². In this approximation the neutrinos don't share in the energy transferred from the annihilating e^± pairs to the CBR photons so that in the post-e^± annihilation universe the photons are hotter than the neutrinos by a factor T / T = (11/4)^1/3, and the relativistic energy density is

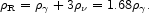(4)

The post-e^± annihilation time-temperature relation is

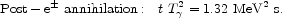(5)

2.1.1. Additional Relativistic Energy Density

One of the most straightforward variations of the standard model of cosmology is to allow for an early (RD) nonstandard expansion rate H' SH, where S H' / H = t / t' is the expansion rate factor. One possibility for S 1 is from the modification of the RD energy density (see Eqs. 2 & 4) due to "extra" relativistic particles X: _{R R} + _X. If the extra energy density is normalized to that which would be contributed by one additional flavor of (decoupled) neutrinos (Steigman, Schramm & Gunn 1977), _X N (N 3 + N), then

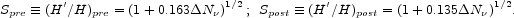(6)

Notice that S and N are related nonlinearly. It must be emphasized that it is S and not N that is the fundamental parameter in the sense that any term in the Friedman equation which scales as radiation, decreasing with the fourth power of the scale factor, will change the standard-model expansion rate (S 1). For example, higher-dimensional effects such as in the Randall-Sundrum model (Randall & Sundrum 1999a) may lead to either a speed-up in the expansion rate (S > 1; N > 0) or, to a slow-down (S < 1; N < 0); see, also, [Randall & Sundrum (1999b)], [Binetruy et al. (2000)], [Cline et al. (2000)].