4.1. Deuterium - The Baryometer Of Choice

The deuteron is the most weakly bound of the light nuclides. As a result, any deuterium cycled through stars is burned to ³He and beyond. Thus, its post-BBN evolution is straightforward: deuterium observed anywhere, anytime, provides a lower bound to the primordial D abundance. For "young" systems, in the sense of little stellar evolution (e.g. sites at high redshift and/or with very low metallicity), the observed D abundance should reach a plateau at the primordial value. Although there are observations of deuterium in the solar system and the interstellar medium (ISM) of the Galaxy which provide interesting lower bounds to its primordial abundance, the observations of relic D in a few, high redshift, low metallicity, QSO absorption line systems (QSOALS) are of most value in estimating its primordial abundance.

While its simple post-BBN evolution is the greatest asset for relic D, the identical absorption spectra of DI and HI (except for the velocity/wavelength shift resulting from the heavier reduced mass of the deuterium atom) is a severe liability, limiting significantly the number of useful targets in the vast Lyman-alpha forest of the QSO absorption spectra (see [Kirkman et al. (2003)] for a discussion). It is essential in choosing a target QSOALS that its velocity structure be "simple" since a low column density HI absorber, shifted by ~ 81 km/s with respect to the main HI absorber (an "interloper") would masquerade as DI absorption. If this is not recognized, a too high D/H ratio would be inferred. Since there are many more low-column density absorbers than those with high HI column densities, absorption systems with somewhat lower HI column density (e.g. Lyman-limit systems: LLS) are more susceptible to this contamination than the higher HI column density absorbers (e.g. damped Ly absorbers: DLA). However, while the DLA have many advantages over the LLS, a precise determination of the HI column density requires an accurate placement of the continuum, which could be compromised by interlopers. This might lead to an overestimate of the HI column density and a concomitant underestimate of D/H (J. Linsky, private communication). As a result of these complications, the path to primordial D using QSOALS has not been straightforward, and some abundance claims have had to be withdrawn or revised. Presently there are only five QSOALS with reasonably firm deuterium detections [Kirkman et al. (2003)] (and references therein); these are shown in Figure 2 along with the corresponding solar system and ISM D abundances. It is clear from Figure 2, that there is significant dispersion among the derived D abundances at low metallicity which, so far, mask the anticipated deuterium plateau. This suggests that systematic errors of the sort described here may have contaminated some of the determinations of the DI and/or HI column densities.

Figure 2. Deuterium abundances, by number with respect to hydrogen D/H, versus metallicity (relative to solar on a log scale) from observations (as of early 2003) of QSOALS (filled circles). "X" is usually silicon or oxygen. Shown for comparison are the D abundances inferred for the local ISM (filled square) and the solar system (presolar nebula: "Sun"; filled triangle).

To explore the possibility that such systematic effects, which would be correlated with the HI column density, may be responsible for at least some of the dispersion revealed in Figure 2, it is useful to plot the same QSOALS data versus the HI column density; this is shown in Figure 3. Indeed, there is the suggestion from this very limited data set that the low column density absorbers (LLS) have high D/H, while the high column density systems (DLA) have low abundances. However, on the basis of extant data it is impossible to decide which, if any, of these systems has been contaminated; there is no justification for excluding any of the present data. Indeed, perhaps the data is telling us that our ideas about post-BBN deuterium evolution need to be revised.

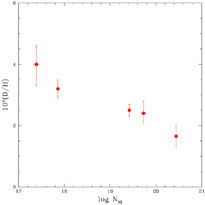Figure 3. Deuterium abundances versus the HI column densities for the corresponding QSOALS shown in Figure 2.

To proceed further using the current data I follow the lead of [O'Meara et al. (2001)] and [Kirkman et al. (2003)] and adopt for the primordial D abundance the weighted mean of the D abundances for the five lines of sight (Kirkman et al. 2003); the dispersion in the data is used to set the error in y_D: y_D = 2.6 ± 0.4. It should be noted that using the same data [Kirkman et al. (2003)] derive a slightly higher mean D abundance: y_D = 2.74. The difference is traced to their first finding the mean of log(y_D) and then using it to compute the mean D abundance (y_D 10^<log(y_D)>).

The BBN-predicted relic abundance of deuterium depends sensitively on the baryon density, y_D ^-1.6, so that a ~ 10% determination of y_D can be used to estimate the baryon density to ~ 6%. For SBBN (S = 1 (N = 3), _e = 0), the adopted primordial D abundance corresponds to ₁₀(SBBN) = 6.10^+0.67_-0.52 (_B h² = 0.0223^+0.0024_-0.0019), in spectacular agreement with the [Spergel et al. (2003)] estimate of ₁₀ = 6.14 ± 0.25 (_B h² = 0.0224 ± 0.0009) based on WMAP and other CBR data (ACBAR and CBI) combined with large scale structure (2dFGRS) and Lyman-alpha forest constraints. Indeed, if the [Spergel et al. (2003)] estimate is used for the BBN baryon density, the BBN-predicted deuterium abundance is y_D = 2.57 ± 0.27 (where a generous allowance of ~ 8% has been made for the uncertainty in the BBN prediction at fixed ; for the [Burles, Nollett & Turner (2001)] nuclear cross sections and uncertainties the result is y_D = 2.60^+0.20_-0.18).