2.6. Starbursts

2.6.1. What are they?

Starbursts are galaxies (sometimes, the term also refers only to particular regions of galaxies) undergoing a large-scale star formation episode. They feature strong infrared emission originating in the high levels of interstellar extinction, strong HII-region-type emission-line spectrum (due to a large number of O and B-type stars), and considerable radio emission produced by recent SNRs. Typically, starburst regions are located close to the galactic center, in the central kiloparsec. This region alone can be orders of magnitude brighter than the center of normal spiral galaxies. From such an active region, a galactic-scale superwind is driven by the collective effect of supernovae and particular massive star winds. The enhanced supernova explosion rate creates a cavity of hot gas (~ 10⁸ K) whose cooling time is much greater than the expansion time scale. Since the wind is sufficiently powerful, it can blow out the interstellar medium of the galaxy preventing it from remaining trapped as a hot bubble. As the cavity expands, a strong shock front is formed on the contact surface with the cool interstellar medium. The shock velocity can reach several thousands of kilometers per second and ions like iron nuclei can be efficiently accelerated in this scenario, up to ultrahigh energies, by Fermi's mechanism [301]. If the super-GZK particles are heavy nuclei from outside our Galaxy, then the nearby (~ 3 Mpc [302]) starburst galaxies M82 (l = 141°, b = 41°) and NGC 253 (l = 89°, b = -88°) are prime candidates for their origin.

2.6.2. M82 and NGC253

M82 is probably the best studied starburst galaxy, located at only 3.2 Mpc. The total star formation rate in the central parts is at least ~ 10 M yr^-1 [303]. The far infrared luminosity of the inner region within 300 pc of the nucleus is ~ 4 × 10¹⁰ L [304]. There are ~ 1 × 10⁷ M of ionized gas and ~ 2 × 10⁸ M of neutral gas in the IR source [304, 305]. The total dynamical mass in this region is ~ (1 - 2) × 10⁹ M [305]. The main observational features of the starburst can be modelled with a Salpeter IMF extending from 0.1 to 100 M. The age of the starburst is estimated in ~ (1 - 3) × 10⁷ yr [304]. Around ~ 2.5 × 10⁸ M (i.e. ~ 36 % of the dynamical mass) is in the form of new stars in the burst [305]. The central region, then, can be packed with large numbers of early-type stars.

NGC 253 has been extensively studied from radio to -rays (e.g. [306, 307, 308]). A TeV detection was reported by CANGAROO [309], but has been yet unconfirmed by other experiments. More than 60 individual compact radio sources have been detected within the central 200 pc [310], most of which are supernova remnants (SNRs) of only a few hundred years old. The supernova rate is estimated to be as high as 0.2 - 0.3 yr^-1, comparable to the massive star formation rate, ~ 0.1 M yr^-1 [310, 311]. The central region of this starburst is packed with massive stars. Four young globular clusters near the center of NGC 253 can account for a mass well in excess of 1.5 × 10⁶ M [312, 313]. Assuming that the star formation rate has been continuous in the central region for the last 10⁹ yrs, and a Salpeter IMF for 0.08-100 M, the bolometric luminosity of NGC 253 is consistent with 1.5 × 10⁸ M of young stars [312]. Based on this evidence, it appears likely that there are at least tens of millions of young stars in the central region of the starburst. These stars can also contribute to the -ray luminosity at high energies [314, 138]. Physical, morphological, and kinematic evidence for the existence of a galactic superwind has been found for NGC 253 [315]. Shock interactions with low and high density clouds can produce X-ray continuum and optical line emission, respectively, both of which have been directly observed.

A region about 1 kpc of the M82 galactic center appears to be a fossil starburst, presenting a main sequence stellar cutoff corresponding to an age of 100-200 Myr and a current average extinction of 0.6 mag (compare with the extinction of the central and current starburst region, 2.2 mag) whereas, nearby globular glusters age estimations are between 2 × 10⁸ and 10⁹ yr [316]. It appears possible for this galaxy, then, that a starburst (known as M82 "B") of similar amplitude than the current one was active in the past.

2.6.3. Two-step acceleration-process in starbursts

The acceleration of particles in starburst galaxies is thought to be a two-stage process [301]. First, ions are thought to be diffusively accelerated at single SNRs within the nuclear region of the galaxy. Energies up to ~ 10^14-15 eV can be achieved in this step (see, e.g. [317]). Due to the nature of the central region, and the presence of the superwind, the escape of the iron nuclei from the central region of the galaxy is expected to be dominated by convection. ⁽²⁴⁾ Collective plasma motions of several thousands of km per second and the coupling of the magnetic field to the hot plasma forces the CR gas to stream along from the starburst region. Most of the nuclei then escape through the disk in opposite directions along the symmetry axis of the system, being the total path travelled substantially shorter than the mean free path.

Once the nuclei escape from the central region of the galaxy they are injected into the galactic-scale wind and experience further acceleration at its terminal shock. CR acceleration at superwind shocks was firstly proposed in Ref. [319] in the context of our own Galaxy. The scale length of this second shock is of the order of several tens of kpc (see Ref. [302]), so it can be considered as locally plane for calculations. The shock velocity v_sh can be estimated from the empirically determined superwind kinetic energy flux 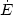_sw and the mass flux generated by the starburst through: 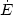_sw = 1/2 v_sh². The shock radius can be approximated by r v_sh , where is the starburst age. Since the age is about a few tens of million years, the maximum energy attainable in this configuration is constrained by the limited acceleration time arisen from the finite shock's lifetime. For this second step in the acceleration process, the photon field energy density drops to values of the order of the cosmic background radiation (we are now far from the starburst region), and consequently, iron nuclei are safe from photodissociation while energy increases to ~ 10²⁰ eV.

To estimate the maximum energy that can be reached by the nuclei, consider the superwind terminal shock propagating in a homogeneous medium with an average magnetic field B. If we work in the frame where the shock is at rest, the upstream flow velocity will be v₁ (|v₁| = v_sh) and the downstream velocity, v₂. The magnetic field turbulence is assumed to lead to isotropization and consequent diffusion of energetic particles which then propagate according to the standard transport theory [320]. The acceleration time scale is then [321]: t_acc = 4 / v₁² where is the upstream diffusion coefficient which can be written in terms of perpendicular and parallel components to the magnetic field, and the angle between the (upstream) magnetic field and the direction of the shock propagation: = _|| cos² + sin². Since strong turbulence is expected from the shock we can take the Bohm limit for the upstream diffusion coefficient parallel to the field, i.e. _|| = 1/3 E / Z e B₁, where B₁ is the strength of the pre-shock magnetic field and E is the energy of the Z-ion. For the component we shall assume, following Biermann [322], that the mean free path perpendicular to the magnetic field is independent of the energy and has the scale of the thickness of the shocked layer (r / 3). Then, = 1/3 r(v₁ - v₂) or, in the strong shock limit, = rv₁² / 12. The upstream time scale is t_acc ~ r / (3v₁), r / 3v₁ = 4 / v₁² (E / (3ZeB₁) cos² + rv₁² / 12sin² ). Thus, using r = v₁ and transforming to the observer's frame one obtains

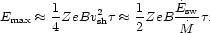(52)

The predicted kinetic energy and mass fluxes of the starburst of NGC 253 derived from the measured IR luminosity are 2 × 10⁴² erg s^-1 and 1.2 M yr^-1, respectively [302]. The starburst age is estimated from numerical models that use theoretical evolutionary tracks for individual stars and make sums over the entire stellar population at each time in order to produce the galaxy luminosity as a function of time [304]. Fitting the observational data these models provide a range of suitable ages for the starburst phase that, in the case of NGC 253, goes from 5 × 10⁷ to 1.6 × 10⁸ yr (also valid for M82) [304]. These models must assume a given initial mass function (IMF), which usually is taken to be a power-law with a variety of slopes. Recent studies has shown that the same IMF can account for the properties of both NGC 253 and M82 [323]. Finally, the radio and -ray emission from NGC 253 are well matched by models with B ~ 50µG [307]. With these figures, already assuming a conservative age = 50 Myr, one obtains a maximum energy for iron nuclei of E_max^Fe > 3.4 × 10²⁰ eV.

2.6.4. The starburst hypothesis: UHECR-luminosity and correlations

For an extragalactic, smooth, magnetic field of 15 - 20 nG, diffusive propagation of nuclei below 10²⁰ eV evolves to nearly complete isotropy in the CR arrival directions [324, 325]. Thus, we could use the rates at which starbursts inject mass, metals and energy into superwinds to get an estimate on the CR-injection spectra. Generalizing the procedure discussed in Sec. 2.4.3 - using equal power per decade over the interval 10^18.5 eV < E < 10^20.6 eV - we obtain a source CR-luminosity

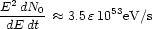(53)

where is the efficiency of ultra high energy CR production by the superwind kinetic energy flux. With this in mind, the energy-weighted approximately isotropic nucleus flux at 10¹⁹ eV is given by [324]

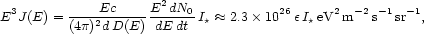(54)

where I_* = I_M82 + I_{NGC 253}. To estimate the diffusion coefficient we used B_nG = 15, _Mpc = 0.5, and an average Z = 20. We fix

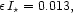(55)

after comparing Eq. (54) to the observed CR-flux. Note that the contribution of I_M82 and I_{NGC 253} to I_* critically depends on the age of the starburst. The relation "starburst-age/superwind-efficiency" derived from Eq. (55), leads to 10%, if both M82 and NGC 253 were active for 115 Myr. The power requirements may be reduced assuming contributions from M82 "B" [324].

Above > 10^20.2 eV iron nuclei do not propagate diffusively. Moreover, the CR-energies get attenuated by photodisintegration on the CMB and the intergalactic infrared background photons. However, the energy-weighted flux beyond the GZK-energy due to a single M82 flare

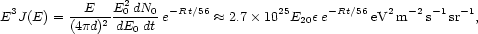(56)

is easily consistent with observation [324]. Here, R is the effective nucleon loss rate of the nucleus on the CBM [94].

In the non-diffusive regime (i.e., 10^20.3 eV E 10^20.5 eV), the accumulated deflection angle from the direction of the source in the extragalactic B-field is roughly 10° 20° [325]. The nuclei suffer additional deflection in the Galactic magnetic field. In particular, if the Galactic field is of the ASS type, the arrival direction of the 4 highest energy CRs can be traced backwards to one of the starbursts [326]. Figure 8 shows the extent to which the observed arrival directions of the highest energy CRs deviate from their incoming directions at the Galactic halo because of bending in the magnetic field given in Eq. (13). The incoming CR trajectories are traced backwards up to distances of 20 kpc away from the Galactic center, where the effects of the magnetic field is negligible. The diamond at the head of each solid line denotes the observed arrival direction, and the points along these lines indicate the direction from which different nuclear species (with increasing mass) entered the Galactic halo. In particular, the tip of the arrows correspond to incoming directions at the halo for iron nuclei, whereas the circles correspond to nuclei of neon. Regions within the dashed lines comprise directions lying within 20° and 30° degrees of the starbursts. It is seen that trajectories for CR nuclei with Z 10 can be further traced back to one of the starbursts, within the uncertainty of the extragalactic deviation.

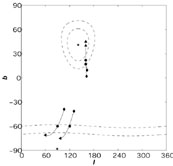Figure 8. Left: Directions in Galactic coordinates of the four highest energy CRs at the boundary of the Galactic halo. The diamonds represent the observed incoming directions. The circles and arrows show the directions of neon and iron nuclei, respectively, before deflection by the Galactic magnetic field. The solid line is the locus of incoming directions at the halo for other species with intermediate atomic number. The stars denote the positions of M82 and NGC253. The dashed lines are projections in the (l, b) coordinates of angular directions within 20° and 30° of the starbursts. Right: Curves of constant probabilities in the two-dimensional parameter space defined by the size of the cone and the minimum number of events originating within the resulting effective solid angle [326].

The effects of the BSS configuration are completely different. Because of the averaging over the frequent field reversals, the resulting deviations of the CR trajectories are markedly smaller, and in the wrong direction for correlation of current data with the starburst sources. We note that the energy-ordered 2D correlation distribution of the AGASA data is in disagreement with expectations for positively charged particles and the BSS configuration [296].

We now attempt to assess to what extent these correlations are consistent with chance coincidence. We arrive at the effective angular size of the source in a two-step process. Before correcting for bias due to the coherent structure of the Galactic magnetic field, the deflections in the extragalactic and Galactic fields (regular and random components) may be assumed to add in quadrature, so that the angular sizes of the two sources are initially taken as cones with opening half-angles between 40° and 60°, which for the purpose of our numerical estimate we approximate to 50°. However, the global structure of the field will introduce a strong bias in the CR trajectories, substantially diminishing the effective solid angle. The combined deflections in the l and b coordinates mentioned above concentrate the effective angular size of the source to a considerably smaller solid angle. As a conservative estimate, we retain 25% of this cone as the effective source size. A clear prediction of this consideration is then that the incoming flux shows a strong dipole anisotropy in the harmonic decomposition.

Now, by randomly generating four CR positions in the portion of the sky accessible to the existing experiments (declination range > -10°), an expected number of random coincidences can be obtained. The term "coincidence" is herein used to label a synthetic CR whose position in the sky lies within an effective solid angle _eff of either starburst. _eff is characterized by a cone with opening half-angle reduced from 50° to 24° to account for the 75% reduction in effective source size due to the magnetic biasing discussed above. Cosmic ray positional errors were considered as circles of 1.6° radius for AGASA. For the other experiments the asymmetric directional uncertainty was represented by a circle with radius equal to the average experimental error. The random prediction for the mean number of coincidences is 0.81 ± 0.01. The Poisson probability ⁽²⁵⁾ for the real result to be no more than the tail of the random distribution is 1%. Alternatively, we may analyze this in terms of confidence intervals. For the 4 observed events, with zero background, the Poisson signal mean 99% confidence interval is 0.82 - 12.23 [279]. Thus our observed mean for random events, 0.81 ± 0.01, falls at the lower edge of this interval, yielding a 1% probability for a chance occurrence. Of course, this is not compelling enough to definitively rule out chance probability as generating the correlation of the observed events with the candidate sources, but it is suggestive enough to deserve serious attention in analyses of future data.

Assuming an extrapolation of AGASA flux (E³ J_obs(E)) up to 10^20.5 eV, the event rate at Pampa Amarilla ⁽²⁶⁾ is given by

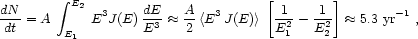(57)

where E₁ = 10^20.3 eV and E₂ = 10^20.5 eV. Considering a 5-year sample of 25 events and that for this energy range the aperture of PAO is mostly receptive to cosmic rays from NGC 253, we allow for different possibilities of the effective reduction of the cone size because of the Galactic magnetic field biasing previously discussed. In Fig. 8 we plot contours of constant probabilities (P = 10^-4, 10^-5) in the two-dimensional parameter space of the size of the cone (as a fraction of the full 50° circle) and the minimum number of events originating within the resulting effective solid angle. The model predicts that after 5 years of operation, all of the highest energy events would be observed in the aperture described above. Even if 7 or 8 are observed, this is sufficient to rule out a random fluctuation at the 10^-5 level. Thus, a clean test of the starburst hypothesis can be achieved at a very small cost: < 10^-5 out of a total 10^-3 PAO probability budget [327].

²⁴ The relative importance of convection and diffusion in the escape of the CRs from a region of disk scale height h is given by the dimensionless parameter, q = V₀ h / ₀, where V₀ is the convection velocity and ₀ is the CR diffusion coefficient inside the starburst [318]. When q 1, the CR outflow is difussion dominated, whereas when q 1 it is convection dominated. For the central region of NGC 253 a convection velocity of the order of the expanding SNR shells ~ 10000 km s^-1, a scale height h ~ 35 pc, and a reasonable value for the diffusion coefficient ₀ ~ 5 × 10²⁶ cm² s^-1 [179], lead to q ~ 216. Thus, convection dominates the escape of the particles. The residence time of the iron nuclei in the starburst results t_RES ~ h / V₀ 1 × 10¹¹ s. Back.

²⁵ Because of constraints inherent in partitioning events among clusters, the distributions are very close to, but not precisely Poisson [65]. Back.

²⁶ The Southern Site of PAO has been christened Pampa Amarilla. Recall that it has an aperture A 7000 km² sr for showers with incident zenith angle less than 60°. Back.