4. WHEN DO GALAXIES BECOME FIRST OPAQUE?

On a cosmological scale, the formation and evolution of dust in galaxies and damped Ly (DLA) systems has been a subject of considerable interest with the goals of studying the following: the effects of dust on the rate of various dust-related physical processes in their ISM such as the formation of H₂ [31]; the obscuration of quasars [24, 8]; the relation between the dust abundance and galaxy metallicity [47, 19]; the depletion of elements in DLA systems [38, 39]; and the evolution of the IR emission seen in the diffuse extragalactic background light [57].

Also a subject of great interest is when galaxies became first opaque, opacity being defined in a bolometric sense as the fraction of total starlight energy that is processed by dust into IR emission. Observations of ultraluminous IR galaxies at redshifts of ~ 3 [23, 34] and the detection of large quantities of dust in high-redshift objects [14], suggest that dust formation occurred early and efficiently after the onset of galaxy formation. The need for rapid dust formation has led Dunne et al. [14] to propose that massive, rapidly evolving stars must be responsible for the dust observed at high redshifts. This seems to be supported by the fact that dust production in AGB stars is delayed by a few hundred million years, compared to the production by SNe (see Figure 7). Furthermore, the yield of dust in AGB stars may be quite lower than that depicted in Figure 2. But what is the dust yield from SNe? Observations of Cas A with the ISO [45, 3] and Spitzer satellites [30, 43] show that the total mass of SN condensed dust is less than ~ 0.2 M, which is only about 10%, of the total amount of refractory elements that formed in the ejecta. Using SCUBA submillimeter observations of the remnant, Dunne et al. [14] claimed to have detected a large mass (M 2 - 20 M, depending on the adopted dust properties) of cold dust in the ejecta of Cas A. This large amount of dust exceeds the amount of refractory elements produced in the explosion [22]. Subsequent observations with the Spitzer satellite, and comparison of the SCUBA data with molecular line observations revealed that the submillimeter emission from the direction of Cas A is actually emitted from a molecular cloud along the line of sight to the remnant, instead of the ejecta [43, 65]. The total mass of dust produced in SNe may therefore also be lower by a factor between 5 and 10 from those depicted in Figure 3. The question of what dust is responsible for the rise in galactic opacity will depend therefore on details of the dust evolution model. On one hand, SNe do indeed form the first dust, but on the other hand, carbon particles are significantly more opaque than silicates, potentially offsetting the advantage of SN condensates. What dust particles are ultimately responsible for producing the UV-optical opacity in galaxies will therefore depend on the relative yields of SN- and AGB-condensed dust, and their subsequent evolution. Here we will only present a very preliminary investigation into this issue.

We will assume that galaxies first become opaque when the radial visual optical depth of molecular clouds in which most of the star formation takes place exceeds unity. The radial opacity of a cloud at V is given by:

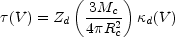(1)

where Z_d is the dust-to-gas mass ratio, M_c the mass of the cloud, R_c its radius, and _d is the mass absorption coefficient of the dust. The criteria we adopt here is obviously a simplified one, since many overlapping optically thin molecular clouds can create an effectively opaque line-of-sight to star forming regions. Nevertheless, this criterion is useful for this simple analysis. Numerically, the expression for (V) is approximately given by:

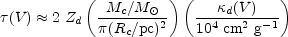(2)

Dust opacities at V are [11]:

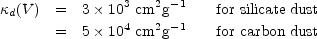(3) (4)

The surface density of molecular clouds in normal galaxies exhibits a narrow spread in values, ranging from about 10 to 100 M pc^-2 [33]. In luminous IR galaxies (LIRGs) star formation seems to take place in clouds with higher surface densities of about 10³ to 10⁴ M pc^-2 [58].

Adopting a cloud surface density of 5 × 10³ M pc^-2 we get that actively star forming galaxies will become first opaque when (V) 1, or when

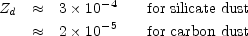(5)

From Figure 7 we get that the critical metallicity for carbon dust is reached when the time lapse since the onset of star formation, t, is about 100 Myr, and that SN-condensed carbon dominates the abundance of carbon dust in the ISM. If only AGB stars produced carbon dust, then silicate dust particles will provide the first significant opacity and reach the critical metallicity at t 400 Myr. Carbon produced in AGB stars will reach the critical carbon metallicity later, at t 500 Myr. Adopting a standard CDM cosmology with a Hubble constant of 70 km s^-1 Mpc^-1, = 0.73, and _m = 0.27, we get that the rate at which the universe ages as a function of redshift z is given, to an accuracy of ~ 4%, by:

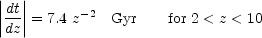(6)

If the SSP first formed at z = z_s, the the universe became first opaque at a redshift z₌₁ given by:

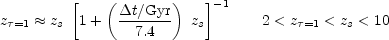(7)

Figure 10 shows the exact relation between z_s and z₌₁ for different values of t. For the simple model adopted here, the figure shows that a galaxy formed at redshift z_s = 10, will become opaque at z₌₁ 8.8 if t = 100 Myr, and at z₌₁ 5.9 if t = 500 Myr. The actual value of t depends on the chemical evolution model, the condensation efficiencies of carbon and silicate dust in the different sources, and the star formation history of the galaxy.

Figure 10. The redshift z=1, at which a galaxy becomes opaque (as defined in the text) as a function of the redshift zs at which the galaxy first formed. The different curves are labeled by t(Gyr), the time required for the dust abundance to be sufficiently high to cause typical molecular clouds to become opaque.