2.2. Surface brightness, radial scale, and absolute magnitude

From the value of µ_e, the `effective surface brightness' at R_e, and knowing the value of n, one can compute both the central surface brightness µ₀ and the average/mean surface brightness <µ>_e within the effective radius.

At the centre of the profile one has, from Equation (6),

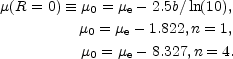
(7)

The difference between µ_e and µ₀ is shown in Figure (2) as a function of the Sérsic index n.

Figure 2. Top panel: Difference between the central surface brightness µ0 and the effective surface brightness µe as a function of profile shape n. Bottom panel: Difference between µe and the mean effective surface brightness <µ>e as a function of n.

The `mean effective surface brightness', often simply referred to as the `mean surface brightness', is computed as follows. The average intensity, <I>_e, within the effective radius is obtained by integrating the intensity over the area A = R_e² such that

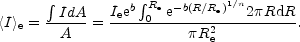
Letting x = b(R / R_e)^1/n, one has

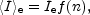
where

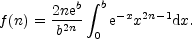
Now as b was chosen such that R_e is the radius containing half of the total light, one has

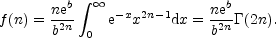
(8)

Thus,

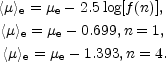
(9)

The difference between µ_e and <µ>_e is shown in Figure (2) as a function of the Sérsic index n (Caon et al. 1994; Graham & Colless 1997).

Substituting equation 9 into Equation 5, one has, at R = R_e,

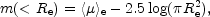
(10)

and thus ⁴

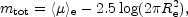
(11)

This expression can be rewritten in terms of the absolute magnitude, M_tot, the effective radius in kpc, R_{e, kpc}, and the absolute effective surface brightness, <µ>_{e, abs}, (i.e., the mean effective surface brightness if the galaxy was at a distance of 10pc):

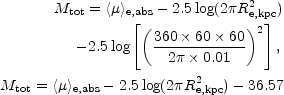
(12)

The apparent and absolute mean effective surface brightnesses are related by the cosmological corrections:

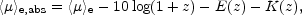
(13)

where z, E(z), and K(z) are the redshift, evolutionary correction, and K-correction respectively (e.g., Driver et al. 1994 and references therein).

Another transformation arises from the use of scale-lengths h rather than effective radii R_e. When the R^1/n model is written as

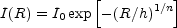
(14)

(e.g., Ellis & Perry 1979, their page 362; Davies et al. 1988), where I₀ = I(R = 0), one has

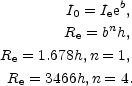
(15) (16)

It's straightforward to show that

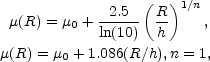
(17)

and

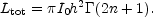
(18)

Given the small scale-lengths associated with the n = 4 model, and the practical uncertainties in deriving a galaxy's central brightness, one can appreciate why Equation (1) is preferred over Equation (14).

If one is modelling a two-component spiral galaxy, consisting of an exponential disk and an R^1/n bulge, then the bulge-to-disk luminosity ratio is given by the expression

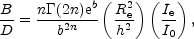
(19)

where h and I₀ are respectively the scale-length and central intensity of the disk, and R_e, I_e, and n describe the Sérsic bulge profile. Noting that 2n (2n) = (2n + 1) = (2n)!, the above equation can be simplified for integer values of 2n. For those who are curious, the first term on the right hand side of the equality can be seen plotted as a function of n in Graham (2001a).

⁴ Using empirical measurements within some suitably large aperture, one has from simple geometry that <µ>_1/2 = m_{tot, ap} + 2.5 log(2 R_1/2²). Expressions to correct these approximate values -- due to the missed flux outside of one's chosen aperture -- are given in Graham et al. (2005). Back.