Annu. Rev. Astron. Astrophys. 2002. 40: 539-577 Copyright © 2002 by Annual Reviews. All rights reserved

2.1. X-ray properties of clusters

Observations of galaxy clusters in the X-ray band have revealed a substantial fraction, ~ 15%, of the cluster mass to be in the form of hot diffuse gas, permeating its potential well. If this gas shares the same dynamics as member galaxies, then it is expected to have a typical temperature

(3)

where m_p is the proton mass and µ is the mean molecular weight (µ = 0.6 for a primordial composition with a 76% fraction contributed by hydrogen). Observational data for nearby clusters (e.g. Wu et al. 1999) and for distant clusters (see Figure 2) actually follow this relation, although with some scatter and with a few outliers. This correlation indicates that the idealized picture of clusters as relaxed structures in which both gas and galaxies feel the same dynamics is a reasonable representation. There are some exceptions that reveal the presence of a more complex dynamics.

Figure 2. Left The relation between galaxy velocity dispersion, v, and ICM temperature, T, for distant (z > 0.15) galaxy clusters. Velocity dispersions are taken from Carlberg et al. (1997a) for CNOC clusters and from Girardi & Mezzetti (2001) for MS1054-03 and RXJ1716+67. Temperatures are taken from Lewis et al. (1999) for CNOC clusters, from Jeltema et al. (2001) for MS1054-03 and from Gioia et al. (1999) for RXJ1716+67. The solid line shows the relation kBT = µ mp v2, and the dashed line is the best-fit to the low-z T-v relation from Wu et al. (1999). Right The low-z relation between X-ray luminosity and the mass contained within the radius encompassing an average density 200 c (from Reiprich & Böhringer 2002). The two lines are the best log-log linear fit to two different data sets indicated with filled and open circles.

At the high energies implied by Equation 3, the ICM behaves as a fully ionized plasma, whose emissivity is dominated by thermal bremsstrahlung. The emissivity for this process at frequency scales as n_e n_i g(, T) T^-1/2 exp(- h / k_B T), where n_e and n_i are the number density of electrons and ions, respectively, and g(, T) ln(k_B T / h ) is the Gaunt factor. Whereas the pure bremsstrahlung emissivity is a good approximation for T 3 keV clusters, a further contribution from metal emission lines should be taken into account when considering cooler systems (e.g. Raymond & Smith 1977). By integrating the above equation over the energy range of the X-ray emission and over the gas distribution, one obtains X-ray luminosities L_X ~ 10⁴³-10⁴⁵ erg s^-1. These powerful luminosities allow clusters to be identified as extended sources out to large cosmological distances.

Assuming spherical symmetry, the condition of hydrostatic equilibrium connects the local gas pressure p to its density _gas according to

(4)

By inserting the equation of state for a perfect gas, p = _gas k_B T / µ m_p into Equation (4), one can express, M( < R), the total gravitating mass within R as

(5)

If R is the virial radius, then at redshift z we have M R³ 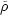₀(1 + z)³ _vir(z), where 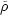₀ is the mean cosmic density at present time and _vir(z) is the mean overdensity within a virialized region (see also Equation 13, below). For an Einstein-de-Sitter cosmology, _vir is constant and therefore, for an isothermal gas distribution, Equation (5) implies T M^2/3(1 + z).

Such relations show how quantities, such as _gas and T, which can be measured from X-ray observations, are directly related to the cluster mass. Thus, in addition to providing an efficient method to detect clusters, X-ray studies of the ICM allow one to measure the total gravitating cluster mass, which is the quantity predicted by theoretical models for cosmic structure formation.

A popular description of the gas density profile is the -model,

(6)

which was introduced by Cavaliere & Fusco-Femiano (1976; see also Sarazin 1988, and references therein) to describe an isothermal gas in hydrostatic equilibrium within the potential well associated with a King dark-matter density profile. The parameter is the ratio between kinetic dark-matter energy and thermal gas energy (see Equation 3). This model is a useful guideline for interpreting cluster emissivity, although over limited dynamical ranges. Now, with the Chandra and Newton-XMM satellites, the X-ray emissivity can be mapped with high angular resolution and over larger scales. These new data have shown that Equation 6 with a unique value cannot always describe the surface brightness profile of clusters (e.g. Allen et al. 2001).

Kaiser (1986) described the thermodynamics of the ICM by assuming it to be entirely determined by gravitational processes, such as adiabatic compression during the collapse and shocks due to supersonic accretion of the surrounding gas. As long as there are no preferred scales both in the cosmological framework (i.e. _m = 1 and power-law shape for the power spectrum at the cluster scales), and in the physics (i.e. only gravity acting on the gas and pure bremsstrahlung emission), then clusters of different masses are just a scaled version of each other. Because bremsstrahlung emissivity predicts L_X M _gas T^1/2, L_X T_X²(1 + z)^3/2 or, equivalently L_X M^4/3(1 + z)^7/2. Furthermore, if we define the gas entropy as S = T / n^2/3, where n is the gas density assumed fully ionized, we obtain S T(1 + z)^-2.

It was soon recognized that X-ray clusters do not follow these scaling relations. As we discuss in Section 5, below, the observed luminosity-temperature relation for clusters is L_X T³ for T 2 keV, and possibly even steeper for T 1 keV groups. This result is consistent with the finding that L_X M with 1.8 ± 0.1 for the observed mass-luminosity relation (e.g. Reiprich & Böhringer 2002; see right panel of Figure 2). Furthermore, the low-temperature systems are observed to have shallower central gas-density profiles than the hotter systems, which turns into an excess of entropy in low-T systems with respect to the S T predicted scaling (e.g. Ponman et al. 1999, Lloyd-Davies et al. 2000).

A possible interpretation for the breaking of the scaling relations assumes that the gas has been heated at some earlier epoch by feedback from a non-gravitational astrophysical source (Evrard & Henry 1991). This heating would increase the entropy of the ICM, place it on a higher adiabat, prevent it from reaching a high central density during the cluster gravitational collapse and, therefore, decrease the X-ray luminosity (e.g. Balogh et al. 1999, Tozzi & Norman 2001, and references therein). For a fixed amount of extra energy per gas particle, this effect is more prominent for poorer clusters, i.e. for those objects whose virial temperature is comparable with the extra-heating temperature. As a result, the self-similar behavior of the ICM is expected to be preserved in hot systems, whereas it is broken for colder systems. Both semi-analytical works (e.g. Cavaliere et al. 1998, Balogh et al. 1999, Wu et al. 2000; Tozzi et al. 2001) and numerical simulations (e.g. Navarro et al. 1995, Brighenti & Mathews 2001, Bialek et al. 2001, Borgani et al. 2001a) converge to indicate that ~ 1 keV per gas particle of extra energy is required. A visual illustration of the effect of pre-heating is reported in Figure 3, which shows the entropy map for a high-resolution simulation of a system with mass comparable to that of the Virgo cluster, for different heating schemes (Borgani et al. 2001b). The effect of extra energy injection is to decrease the gas density in central cluster regions and to erase the small gas clumps associated with accreting groups.

Figure 3. Map of gas entropy from hydrodynamical simulations of a galaxy cluster (from Borgani et al. 2001a). (Left): gravitational heating only. (Right): entropy floor of 50 keV / cm2 imposed at z = 3, corresponding to about 1 keV/part. Light colors correspond to low entropy particles, and dark blue corresponds to high-entropy gas.

The gas-temperature distributions in the outer regions of clusters are not affected by gas cooling. These temperature distributions have been studied with the ASCA and Beppo-SAX satellites. General agreement about the shape of the temperature profiles has still to be reached (e.g. Markevitch et al. 1998, White 2000, Irwin & Bregman 2000). De Grandi & Molendi (2002) analyzed a set of 21 clusters with Beppo-SAX data and found the gas to be isothermal out to ~ 0.2R_vir, with a significant temperature decline at larger radii. Such results are not consistent with the temperature profiles obtained from cluster hydrodynamical simulations (e.g. Evrard et al. 1996), thus indicating that some physical process is still lacking in current numerical descriptions of the ICM. Deep observations with Newton-XMM and Chandra will allow the determination of temperature profiles over the whole cluster virialized region.

X-ray spectroscopy is a powerful means for analyzing the metal content of the ICM. Measurements of over 100 nearby clusters have yielded a mean metallicity Z ~ 1/3 Z, largely independent of the cluster temperature (e.g. Renzini 1997, and references therein). The spatial distribution of metals has recently been studied in detail with ASCA and Beppo-SAX data (e.g. White 2000, De Grandi & Molendi 2001). This field will receive a major boost over the next few years particularly with Newton-XMM, which, with a ten-fold improvement in collecting area and much better angular resolution, will be able to map the distribution of different metals in the ICM, such as Fe, S, Si, O.