


Observations show that the CMB contains anisotropies at the 10-5 level, over a wide range of angular scales. These anisotropies are usually expressed by using a spherical harmonic expansion of the CMB sky:
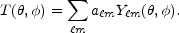 |
The vast majority of the cosmological information is contained in the
temperature 2 point function, i.e., the variance as a
function of separation  .
Equivalently, the power per unit
ln
.
Equivalently, the power per unit
ln  is
is

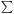 m
|a
m
|a m|2 /
4
m|2 /
4 .
.
The CMB has a mean temperature of
T = 2.725 ± 0.001 K
(1
= 2.725 ± 0.001 K
(1 )
[6],
which can be considered as the monopole component of CMB maps,
a00. Since all mapping experiments involve
difference measurements, they are insensitive to this average level.
Monopole measurements can only be made with absolute temperature
devices, such as the FIRAS instrument on the COBE
satellite
[6].
Such measurements of the spectrum are
consistent with a blackbody distribution over more than
three decades in frequency. A blackbody of the measured temperature
corresponds to
n
)
[6],
which can be considered as the monopole component of CMB maps,
a00. Since all mapping experiments involve
difference measurements, they are insensitive to this average level.
Monopole measurements can only be made with absolute temperature
devices, such as the FIRAS instrument on the COBE
satellite
[6].
Such measurements of the spectrum are
consistent with a blackbody distribution over more than
three decades in frequency. A blackbody of the measured temperature
corresponds to
n =
(2
=
(2 (3) /
(3) /
 2)
T
2)
T 3
3
 411 cm-3 and
411 cm-3 and

 =
(
=
( 2 / 15)
T
2 / 15)
T 4
4
 4.64 ×
10-34 g cm-3
4.64 ×
10-34 g cm-3
 0.260 eV cm-3.
0.260 eV cm-3.
The largest anisotropy is in the
 = 1 (dipole) first
spherical harmonic, with amplitude 3.346 ± 0.017 mK
[5].
The dipole is interpreted to be the result of the Doppler shift caused
by the solar system motion relative to the nearly isotropic blackbody field,
as confirmed by measurements of the velocity field of local galaxies
[7].
The motion of an observer with velocity
= 1 (dipole) first
spherical harmonic, with amplitude 3.346 ± 0.017 mK
[5].
The dipole is interpreted to be the result of the Doppler shift caused
by the solar system motion relative to the nearly isotropic blackbody field,
as confirmed by measurements of the velocity field of local galaxies
[7].
The motion of an observer with velocity
 = v /
c relative to an isotropic Planckian radiation field of
temperature T0 produces a Doppler-shifted temperature
pattern
= v /
c relative to an isotropic Planckian radiation field of
temperature T0 produces a Doppler-shifted temperature
pattern
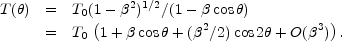 |
At every point in the sky, the spectrum is essentially blackbody, but the spectrum of the dipole is the differential of a blackbody spectrum, as confirmed by Ref. [8].
The implied velocity
[9]
for the solar system barycenter
is v = 368 ± 2 km s-1,
assuming a value T0 =
T , towards
(
, towards
( , b) = (263.85°
± 0.10°, 48.25° ± 0.04°).
Such a solar system velocity implies a
velocity for the Galaxy and the Local Group of galaxies relative
to the CMB. The derived value is
vLG = 627 ± 22 km s-1 toward
(
, b) = (263.85°
± 0.10°, 48.25° ± 0.04°).
Such a solar system velocity implies a
velocity for the Galaxy and the Local Group of galaxies relative
to the CMB. The derived value is
vLG = 627 ± 22 km s-1 toward
( , b) = (276°
± 3°, 30° ± 3°),
where most of the error comes from uncertainty in the velocity of the solar
system relative to the Local Group.
, b) = (276°
± 3°, 30° ± 3°),
where most of the error comes from uncertainty in the velocity of the solar
system relative to the Local Group.
The dipole is a frame dependent quantity, and one can thus determine the `absolute rest frame' of the Universe as that in which the CMB dipole would be zero. Our velocity relative to the Local Group, as well as the velocity of the Earth around the Sun, and any velocity of the receiver relative to the Earth, is normally removed for the purposes of CMB anisotropy study.
Excess variance in CMB maps at higher multipoles
(
 2) is interpreted
as being the result
of perturbations in the energy density of the early Universe,
manifesting themselves at the epoch of the last scattering of the CMB
photons. In the hot Big Bang picture, this happens at a redshift
z
2) is interpreted
as being the result
of perturbations in the energy density of the early Universe,
manifesting themselves at the epoch of the last scattering of the CMB
photons. In the hot Big Bang picture, this happens at a redshift
z  1100,
with little dependence on the details of the model. The process by which the
hydrogen and helium nuclei can hold onto their electrons is usually
referred to as recombination
[10].
Before this epoch, the
CMB photons are tightly coupled to the baryons, while afterwards they
can freely stream towards us.
1100,
with little dependence on the details of the model. The process by which the
hydrogen and helium nuclei can hold onto their electrons is usually
referred to as recombination
[10].
Before this epoch, the
CMB photons are tightly coupled to the baryons, while afterwards they
can freely stream towards us.
Theoretical models generally predict that the
a m modes
are Gaussian
random fields, and all tests are consistent with this simplifying assumption
[11].
With this assumption, and if there is no preferred axis,
then it is the variance of the temperature field which
carries the cosmological information, rather than the values of the
individual
a
m modes
are Gaussian
random fields, and all tests are consistent with this simplifying assumption
[11].
With this assumption, and if there is no preferred axis,
then it is the variance of the temperature field which
carries the cosmological information, rather than the values of the
individual
a ms; in
other words the power spectrum in
ms; in
other words the power spectrum in
 fully characterizes the
anisotropies.
The power at each
fully characterizes the
anisotropies.
The power at each  is
(2
is
(2 + 1)
C
+ 1)
C /
(4
/
(4 ), where
C
), where
C
 <|a
<|a m|2>, and
a statistically isotropic sky means that all ms are equivalent.
We use our estimators of the
C
m|2>, and
a statistically isotropic sky means that all ms are equivalent.
We use our estimators of the
C s to
constrain their expectation values,
which are the quantities predicted by a theoretical model.
For an idealized full-sky observation, the variance of each measured
C
s to
constrain their expectation values,
which are the quantities predicted by a theoretical model.
For an idealized full-sky observation, the variance of each measured
C (the variance of the variance) is
[2 / (2
(the variance of the variance) is
[2 / (2 + 1)]
C2
+ 1)]
C2 .
This sampling uncertainty (known as cosmic variance) comes about because
each
C
.
This sampling uncertainty (known as cosmic variance) comes about because
each
C is
is  2 distributed
with (2
2 distributed
with (2 + 1) degrees
of freedom for our observable volume of the Universe.
For partial sky coverage, fsky, this variance is
increased by
1 / fsky and the modes become partially correlated.
+ 1) degrees
of freedom for our observable volume of the Universe.
For partial sky coverage, fsky, this variance is
increased by
1 / fsky and the modes become partially correlated.
It is important to understand that theories predict the expectation value
of the power spectrum, whereas our sky is a single realization. Hence
the `cosmic variance' is an unavoidable source of uncertainty when
constraining models; it dominates the scatter at lower
 s, while the
effects of instrumental noise and resolution dominate at higher
s, while the
effects of instrumental noise and resolution dominate at higher
 s.
s.
2.4. Angular Resolution and Binning
There is no one-to-one conversion between the angle subtended by a
particular wavevector projected on the sky and multipole
 .
However, a single spherical harmonic
Y
.
However, a single spherical harmonic
Y m
corresponds to angular variations of
m
corresponds to angular variations of
 ~
~
 /
/
 .
CMB maps contain anisotropy information from the size of the map (or in
practice some fraction of that size) down to the
beam-size of the instrument,
.
CMB maps contain anisotropy information from the size of the map (or in
practice some fraction of that size) down to the
beam-size of the instrument,
 . One can think of the
effect of a
Gaussian beam as rolling off the power spectrum with the function
e-
. One can think of the
effect of a
Gaussian beam as rolling off the power spectrum with the function
e- (
( +1)
+1)
 2.
2.
For less than full sky coverage, the
 modes are correlated. Hence,
experimental results are usually quoted as a series of `band powers',
defined as estimators of
modes are correlated. Hence,
experimental results are usually quoted as a series of `band powers',
defined as estimators of
 (
( + 1)
C
+ 1)
C /
2
/
2 over different ranges of
over different ranges of
 . because of the strong
foreground signals in the Galactic Plane, even
`all-sky' surveys, such as COBE and WMAP involve a cut sky.
The amount of binning required to obtain uncorrelated estimates of power
also depends on the map size.
. because of the strong
foreground signals in the Galactic Plane, even
`all-sky' surveys, such as COBE and WMAP involve a cut sky.
The amount of binning required to obtain uncorrelated estimates of power
also depends on the map size.