In this Section, we summarise various sets of observational data which shape our current understanding of reionization (for a detailed review on recent developments, see [82]). These observational probes can be broadly divided into two types: the first set probes the extent and nature of the reionization through observations of the IGM while the second is mostly concerned with direct observations of the sources responsible for reionization.
2.1. Observations related to the state of the IGM
As far as the IGM is concerned, the observational constraints on its ionization and thermal state can be divided broadly into three classes, which are discussed in the next three subsections.
We have discussed in the previous Section that the primary evidence
for the IGM to be ionized at z < 6 comes from the
measurements of GP optical depth in the spectra of QSOs.
Under the assumptions of photoionization equilibrium and
a power-law relation between temperature and density,
the Ly
optical depth
GP arising from a
region of overdensity
at a redshift
z can be written as
 |
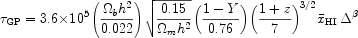(1) |
where Y denotes the helium mass fraction, and
HI
is the neutral hydrogen fraction (defined as the ratio between
neutral hydrogen density and total hydrogen density) at the mean
density = 1. The
exponent of is
determined by the photoionization equilibrium and is given by
= 2.7 -
0.7 
, where
is the
slope of the pressure-density relation. For a isothermal medium
= 1 and
hence GP
2.
All other symbols in the above expression have standard meanings.
This expression clearly shows that for a uniform
medium ( = 1) at
z 
6, the
presence of a neutral hydrogen fraction
HI
10-5
would produce an optical depth of the order unity and hence would show
clear GP absorption trough in the spectra. Since such absorption is not
observed for QSOs at z < 6,
the constraint on the average neutral fraction is
HI <
10-5, which is a robust indication of the fact
that the universe is highly ionized at z < 6.
The observational situation changes for the observed QSOs at z
> 6. The ongoing Sloan Digital Sky Survey (SDSS)
1 has discovered quite
a few QSOs at z
6, the spectra of
which are markedly different from their low-redshift counterparts.
Very long absorption troughs, which are of the size ~ 80-100 comoving Mpc,
have been seen along tens of lines of sight at z > 6
[83,
84,
85,
86,
87,
88].
This implies that the GP optical depth at z
6 is larger than
a few. Unfortunately, such a constraint
does not necessarily imply that the universe is neutral at such redshifts.
For example, a neutral hydrogen fraction
HI ~
10-3 would produce an optical depth
GP ~ 100, more than
what is required to produce the absorption troughs.
This is the typical level of constraint one can obtain through
such model-independent simplistic arguments based on an uniform medium.
Such arguments, though quite effective in giving robust conclusions
at low redshifts, do not yield any strong constraint on the
neutral hydrogen fraction at z
6.
The next line of argument for the approach to the final stages
of reionization at z
6
is based on the change in the slope of the optical
depth [86,
89,
88]
around z ~ 5.5 - 6, which indicates that some qualitative change
in the physics of IGM occurs at these redshifts.
To understand this in simple terms, let us write the neutral hydrogen
fraction
HI in terms
of more physically meaningful quantities:
 |
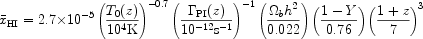(2) |
where T0 is the temperature of the medium at the mean
density
( = 1) and
PI is the
photoionization rate of neutral hydrogen (assumed to be homogeneous).
Combining the above equation with (1), one can see that
GP(z)
(1 + z)1.5 T0-0.7
(z) / PI(z).
Thus when T0 and
PI are
not changing substantially with redshift, we expect
GP(z)
(1 +
z) with
4.5.
This is indeed seen in the observations at
z< 5.5
[90].
However, at higher redshifts, the observations show that
GP evolves much
faster combined with a rapid deviation
from a power-law evolution, thus implying that the properties
of IGM (like T0 and
PI) are
evolving considerably.
This argument points towards a possible phase change in the IGM and
thus suggesting that we are approaching the final stages
of reionization at z
6.
However, one should keep in mind that this argument does not
conclusively prove that the IGM is neutral at z
6 - it
simply indicates for a rapid change in properties. Furthermore, the
above defined GP
is not a directly measured
quantity; one instead measures the mean transmitted flux
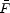which
is computed by integrating the optical depth over all possible
overdensities:
 |
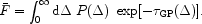(3) |
The quantity
P() denotes
the density distribution of the IGM.
It is thus clear from the above expression that any robust conclusion
based on the observed evolution of
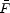would require a good
knowledge of
P().
Hence, the next step for calculating the ionization properties
of the IGM from QSO spectra is to include the density inhomogeneities
in the analysis. From this point on, the conclusions become extremely
model-dependent as we do not have a clear understanding of the density
distribution of the IGM. One approach would be to use numerical simulations
for obtaining the IGM density distribution and
then compute the absorption spectra of high-redshift quasars in the
Ly region
[86].
Using this approach, a rapid evolution of the
volume-averaged neutral fraction of hydrogen has been found at z
6
(HI ~
10-5 at z = 3 to
HI ~
10-3 at z = 6). On the other hand,
a different set of analyses
[91,
92]
from nearly similar data set conclude that
the transmitted fractions have a relatively smooth evolution
over the entire range of redshifts, which can be modeled with a
smoothly decreasing ionization rate; hence no evidence of a
rapid transition could be established.
In addition to the global statistics discussed above,
there are some results based on the transmission
observed in the spectra of individual sources. For example, the
analyses of the spectrum of the most distant known quasar (SDSS
J1148+5251) at an emission redshift of 6.37
show some residual flux both in the
Ly and
Ly troughs,
which when combined with
Ly region
[93],
imply that this flux is consistent with pure
transmission. The presence of unabsorbed regions in the spectrum
corresponds to a highly ionized IGM along that particular line of
sight. However, a complete GP
trough was detected in the spectrum of SDSS J1030+0524 (z = 6.28)
[83],
where no transmitted flux is detected over a large region (300 Å)
immediately blueward of the
Ly emission line. Such
differences in the
ionization state of the IGM along different lines of sight have been
interpreted as a possible signature of the pre-overlap phase of
reionization.
There have been other different approaches to investigate the neutral
hydrogen fraction. For example, one can estimate the
sizes of the ionized regions around the QSOs from the spectra
[94,
95].
Then the neutral gas surrounding the QSO can be modelled as a function
of different parameters: the Strömgren sphere size
RS, the production rate of ionizing photons
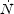ph from the QSO,
the clumping factor of the gas
C and the age of the QSO tage.
Considering 7 QSOs at z
6 (which included
the above cited QSOs), it has been argued that
the small sizes of the ionized regions (~ 10 physical Mpc)
imply that the typical neutral hydrogen fraction of the IGM beyond
z ~ 6 is in the range 0.1 - 1. However, this approach is weighted
down by several uncertainties. For example, one of the uncertainties
is the quasar's production rate of ionizing photons
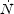ph
as it depends on the shape of the spectral template used.
Moreover it is implicitly assumed in the modelling of clumping factor
that the formation of quasars and galaxies were simultaneous. This in
turn implies that quasars ionize only low density regions and hence
the clumping factor, which regulates the evolution of the ionized regions,
is low. If, instead, stars appears much earlier than QSOs, the quasars
have to ionize high density regions, which means that one should use a
higher value of clumping factor in the calculations
[96].
There has been a different approach based on the damping wings
of the neutral hydrogen
[97].
Using density and velocity fields obtained by
hydrodynamical simulation, the
Ly absorption spectrum
was computed. In this case the neutral hydrogen fraction,
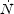ph and
RS are treated as free parameters,
constrained by matching the optical depth observed in the QSO SDSS
J1030+0524. Also in this case, the conclusion is that
the neutral hydrogen fraction is
larger than 10 per cent, i.e., the IGM is significantly more neutral at
z ~ 6 than the lower limit directly obtainable from the GP trough
of the QSO spectrum
(HI
10-3).
However this result is based only on
one quasar. Moreover, the observational constraints on the optical
depth are very uncertain and can introduce errors in the estimates of
HI.
To summarise the QSO absorption line observations -
there is still no robust and model-independent
constraint on the neutral hydrogen fraction from the data.
The spectroscopy
of the Ly forest for
QSOs at z
6 discovered by the SDSS
[84,
87]
strongly suggest that the IGM is highly ionized along some lines of sight.
On the other hand, there are a few (maybe a couple) lines of sight
which seems to indicate that the IGM is neutral, though the
conclusion is still not robust.
In case we find transmission along some lines of sight while the
medium seems quite neutral along others could possibly be interpreted
that the IGM ionization properties are different along different lines
of sight at z
6, thus
suggesting that we might be observing
the end of the reionization process. However, it is also possible that
such dispersion in the IGM properties along different lines of sight
can be accommodated by simply the dispersion in the density inhomogeneities.
As discoveries of more such objects are expected in future,
spectroscopy of high-redshift QSOs remains one of the principal empirical
approaches to understand the final stages of reionization.
Before completing our discussion on the QSO absorption lines, it is
worth mentioning a set of indirect constraints on reionization based on the
temperature of the IGM at z
2 - 4.
2 Using various techniques
like, the lower envelope of the neutral hydrogen column density and
velocity width scatter plot
[98,
99] or wavelet transforms
[100],
one can infer the temperature of the IGM from absorption lines. These
analyses suggest that
T0 ~ 1-2 × 104 K at
z 3, which
in turn imply that hydrogen reionization must occur at z < 9
or else the temperature would be too low to match the
observations. However, one should keep in mind that the analyses has
large uncertainties, like, for example, the dust photoheating of the IGM
could give rise to high temperatures at z
3
[101,
102,
103,
104].
Furthermore, a complex ionization history of helium could relax considerably
the constraints obtained from T0
on the reionization epoch.
2.1.2. Cosmic microwave background radiation
The second most important analysis regarding the reionization
history comes from the observations of temperature and polarization
anisotropies in the cosmic microwave background (CMB) radiation.
As far as the temperature anisotropies are concerned, reionization
can damp the fluctuations on small scales due to photon diffusion
in the ionized plasma. The scattering of photons suppresses the
anisotropies on angular scales below the horizon at the rescattering epoch
by a damping factor
e-el,
where
 |
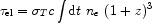(4) |
is the optical depth (measured at the present epoch)
of CMB photons due to Thomson scattering
with free electrons. In the above expression, ne is the
average value of the comoving electron density and
T is
the Thomson scattering cross section.
However, measuring this damping is not easy as it
can be compensated by a larger strength of dark matter density
fluctuations which are measured by the
corresponding power spectrum, usually parametrised
by the two quantities: the primordial spectral index
ns and the fluctuation amplitude at cluster scales
8. Hence, it
is found that
el is only mildly
constrained by the temperature fluctuations
because of strong degeneracies with ns and
8
[105].
For this reason, temperature anisotropy data prior to Wilkinson
Microwave Anisotropy Probe (WMAP)
3 could only constrain
el
0.5
[106].
For sudden reionization models, this only implies that
the redshift of reionization zre
40. To put in
perspective with the discussion of QSO absorption line observations,
reionization at z ~ 6 would imply
el ~ 0.05.
A major breakthrough in our understanding of reionization came after the release of first year WMAP results of polarization measurements. A fundamental prediction of the gravitational instability paradigm is that CMB anisotropies are polarized, i.e., if the temperature anisotropies are produced by primordial fluctuations, their presence at the last scattering surface would polarize the CMB. The generation of polarization requires two conditions to be satisfied: (i) photons need to undergo Thomson scattering off free electrons (the corresponding cross section is polarization-dependent) and (ii) the angular distribution of the photon temperature must have a non zero quadrupole moment. Tight coupling between photons and electrons prior to recombination makes the photon temperature almost isotropic and the generated quadrupole anisotropy, and hence the polarization, is very small. Because the temperature anisotropies are of the order 10-5, the polarization is about 10-6 or less.
To generate a quadrupole, it is
necessary to produce velocity gradients in the
photon-baryon fluid across
the photon mean free path; hence only those
perturbations which have length scales smaller than
the mean free path can produce polarization. At larger scales,
multiple scattering will make the plasma quite homogeneous and thus
no significant quadrupole can be generated, while at much
lower scales polarization is suppressed
due to "Silk damping".
In fact, the polarization generated at the last scattering surface
would be significant at scales comparable to
the horizon size at that epoch (which corresponds
to a multipole number 
~
100), and no polarization signal is expected at larger scales
< 100.
Detection of polarization signal at
< 100 is a clear signature
of secondary processes such as reionization.
Following the completion of
recombination the quadrupole moment of temperature anisotropies
grows due to the photons free streaming. In case these photons are able
to scatter off free electrons at a later stage,
the anisotropy can be transformed into substantial
polarization. This is an ideal effect to probe reionization as it is
the only process which can provide considerable number of free electrons
at post-recombination epochs.
For models with sudden reionization, it can be shown
that the effect dominates on the angular scale of the
horizon at the epoch of reionization. The polarization signal
will peak at a position
zre1/2 with an amplitude proportional to
the total optical depth
el.
Thus the polarization spectrum at low
is
a sensitive probe of the reionization process.
The polarization measurements by the WMAP satellite
[107]
found a significant signal in
the temperature-polarization cross correlation spectrum at
< 10. The position and
the amplitude of this excess
is consistent with an optical depth
el = 0.17 ±
0.04, implying a (sudden) reionization redshift
11 < zre < 30. While this result has
possibly complicated the picture of reionization and thus
generated tremendous amount of activity
within the community, a few subtleties should be kept in mind while
using the reionization constraints: (i) The result is based
on a few points at low
and it is necessary that such an important result is confirmed by
future data. One should also note that the likelihood function for
el
obtained from WMAP data is heavily skewed, probably indicating some sort
of a "tension" within the data. (ii) The constraints on
el depend on the
priors and analysis technique used. For example, fitting the temperature
- E-mode polarization cross power spectrum (TE) to
CDM
models in which all parameters except
el assume their
best fit values based on the temperature power
spectrum (TT), the 68% confidence range obtained is
0.13 < el <
0.21
[107].
Fitting all parameters simultaneously to the TT and the TE data,
the corresponding range changes to obtain
0095 < el <
0.24
[108].
Including additional data external to WMAP, these authors were able to
shrink their confidence interval to
0.11 < el <
0.23. Finally, by assuming that the
observed TT power spectrum is scattered to produce the observed
TE cross-power spectrum, the inferred range is
0.12 < el <
0.20
[107].
(iii) The constraints of
0.17 and
zre
15 usually quoted in the literature assume a sudden reionization.
The constraints can change drastically when this assumption is relaxed.
In case the result is confirmed by future data sets, we note that it is not necessarily contradictory to the QSO results; the history of the luminous sources and their effect on the IGM was probably highly complex, and there was a finite time interval (maybe somewhere around a few hundred million years) from the appearance of the first sources of UV photons and the completion of the reionization.
2.1.3.
Ly emitters at high
redshifts
In parallel, a number of groups have studied star-forming galaxies at
z ~ 6 - 7, and measurements of the
Ly emission line luminosity
function evolution provide another useful observational constraint
[109,
110].
While the QSO absorption
spectra probe the neutral hydrogen fraction regime
xHI 
0.01,
this method is sensitive to the range
xHI ~ 0.1 - 1.0.
Ly emission from
galaxies is expected to be suppressed at redshifts beyond reionization
because of the absorption due to neutral hydrogen, which clearly
affects the evolution of the luminosity function of such
Ly emitters
at high redshifts [111,
109,
112].
Thus a comparison of the luminosity functions
at different redshifts could be used for constraining the reionization.
Through a simple analysis, it was found that the luminosity functions
at z = 5.7 and z = 6.5 are statistically consistent with
one another, thus implying that reionization was largely complete at
z 6.5.
More sophisticated calculations on the evolution of the luminosity
function of Ly emitters
[109,
113,
111]
suggest that the neutral fraction
of hydrogen at z = 6.5 should be less than 50 per cent
[114].
The analysis of the Ly
emitters at high redshifts is complicated by various factors.
(i) Firstly, this suppression of the
Ly emission line
depends on the size of the ionized
region surrounding the source as larger ionized volumes allow
more photons to escape. On the other hand, the sizes of the ionized
regions themselves depend on the clustering properties of the sources.
There is thus a strong coupling between the clustering of the sources,
sizes of the ionized regions and the luminosity function of the
Ly emitters at high
redshifts.
(ii) The ionized hydrogen regions are typically highly asymmetric because
the the ionization-fronts propagate much faster across underdense voids then
across dense filaments. Thus one needs to know the details of the
density distribution around the sources to model the ionized regions.
(iii) It is well known that bright galaxies are biased, so it is likely
that more than one galaxy is located inside a single ionized region;
Ly-emitters can also be
located inside ionized regions of luminous
quasars, which are often many times larger than the ionized regions of
galaxies. It is thus clear that the modelling of the ionized regions
of Ly-emitters is not
straightforward, and hence the reionization
constraints could be severely model-dependent.
2.2. Observations related to the sources of reionization
As we discussed in the Introduction, a major challenge in our understanding of reionization depends on our knowledge of the sources, particularly at high redshifts. In this sense, reionization is closely related to formation of early baryonic structures and thus any observation related to the detection of very distant sources can be important for constraining reionization. In the following, we shall discuss a few most important of such observational probes.
2.2.1. Direct observations of sources at high redshifts
As we understand at present, neither the bright
z 6 QSOs
discovered by the SDSS group
[115]
nor the faint AGN detected in X-ray observations
[116]
produce enough photons to reionize the IGM.
The discovery of star-forming galaxies at z > 6.5
[117,
118,
119]
has resulted in speculation that
early galaxies produce bulk of the ionizing photons for reionization.
However, the spectroscopic studies of I-band dropouts in the Hubble
ultra-deep Field with confirmed redshifts at z
6, indicate
that the measured star formation rate at z = 6 is lower by factor
of 6 from the z = 3 star formation rate.
If the estimate is correct, the I-dropouts do not
emit enough ionizing photons to reionize the universe at z
6
[120].
The short-fall in ionizing photons might be alleviated
by a steep faint-end slope of the luminosity
function of galaxies or a different stellar initial
mass function (IMF); alternatively, the bulk of reionization might
have occurred at z
6 through rapid
star formation in galaxies at much higher redshifts.
There are estimates of a somewhat higher UV luminosity at z = 6 - 10. This is obtained by constructing a luminosity function from ~ 500 galaxies collected from all the deepest wide-area HST data [121]. The luminosity function thus obtained extends 3 magnitudes fainter than the characteristic luminosity L*. This analysis predicts a significant evolution in L* - a doubling from z = 3 to z = 6, thus implying a luminosity density that is only a factor of 1.5 less than the luminosity density at z = 3. The observed evolution is suggestive of that expected from popular hierarchical models, and would seem to indicate that we are literally witnessing the buildup of galaxies in the reionization era.
To summarise, there are somewhat conflicting reports regarding the star
formation rate at z
6 - however, it
is safe to conclude that we have not yet
observed enough number of sources which could ionize the bulk
of the IGM at z
6.
Whether the reionization was actually completed by
galaxies at a much higher redshifts is still an open issue.
2.2.2. Cosmic infrared background radiation
Numerous arguments favour an excess contribution to the extragalactic
background light between 1 µm and a few µm
[122,
123,
124,
125]
when compared to the expectation based on galaxy counts and
Milky Way faint star counts (for a review see
[126]).
While these measurements are likely to be affected by
certain systematics and issues related to the exact contribution
from zodiacal light within
the Solar System, one explanation is that a contribution to the
cosmic infrared background (CIRB) radiation originates
from high redshift sources. The redshifted line emission from
Ly emitting galaxies at
z > 9 would produce an
integrated background in the near-infrared
wavelengths observed today. In case this interpretation of the CIRB is
correct, it would directly constrain the number of ionizing sources
at high redshifts and thus would have direct implications on reionization.
However, if the entire CIRB is due to the high redshift
galaxies, the explanation requires the presence of metal-free
PopIII stars with a top-heavy IMF and possibly a high star-forming
efficiency [127,
128,
129,
130,
131].
In fact, the number of sources required to explain the
CIRB is much higher than that needed to explain the early reionization
constraints. The most serious difficulty in explaining the
CIRB through PopIII stars comes from the observations
of the number of J-dropouts and
Ly
emitters in ultra deep field searches as the models severely
overpredict the number of sources
[132]. At present, the origin
of CIRB remains to be puzzling (as one can discard
other possible sources like miniquasars and decaying neutrinos, see the
next subsection), and it is not clear whether it could have any
significant implications on reionization.
We end this section by briefly reviewing the constraints we have on other kind of sources, namely the Intermediate Mass Black Holes and decaying (exotic) particles.
A large population of intermediate mass black holes (IMBHs) might be
produced at early cosmic times as a left over of the evolution of
very massive first stars. These black holes at high redshifts (z
6)
can, in principle, contribute to the ionization of the
IGM; however they would be accompanied by the
copious production of hard X-ray photons (with energies above
10 keV). The resulting hard X-ray background would redshift and be
observed as a present-day soft X-ray background. One can show that the
observed residual soft X-ray background intensity can put stringent
constraints on the the baryon mass fraction locked into IMBHs and their
growth
[133,
134].
Thus, unless they are extremely X-ray quiet, these black holes, or
miniquasars, must be quite rare and/or have a
short shining phase. As a byproduct, it implies that miniquasars cannot
be the only source of reionization.
The other sources which are popularly invoked to explain reionization
are the exotic particles like decaying neutrinos
[74,
75,
76,
77,
78,
79].
However, in most cases these particles
decay radiatively (producing photons) and hence are severely
constrained by Big Bang Nucleosynthesis, diffuse soft X-ray and
gamma-ray backgrounds and the deviation of the CMB spectrum from
Planckian shape.
For example, the constraints from soft X-ray background limits the
radiatively decaying sterile neutrino mass to
m
< 14
keV and hence the optical depth to Thomson scattering is
el ~ 10-2,
negligible compared to what is required for explaining observations
[81].
Similar constraints exist for other particles, including those
which have decay channels into electrons instead of photons
[80].
The point what comes out from most these analyses is that
different observational constraints leave out a very
small parameter space accessible to the decaying particles and hence their
contribution to reionization may not be that significant.
2 This determination of temperature puts constraints on the reionization of helium too; however, the helium reionization is beyond the scope of this review. Back
3 http://map.gsfc.nasa.gov/ Back