1. THE COSMOLOGICAL PARADIGM AND FRIEDMANN MODEL

Observations show that the universe is fairly homogeneous and isotropic at scales larger than about 150 h^-1 Mpc where 1 Mpc 3 × 10²⁴ cm and h 0.7 is a parameter related to the expansion rate of the universe. The conventional - and highly successful - approach to cosmology separates the study of large scale (l 150 h^-1 Mpc) dynamics of the universe from the issue of structure formation at smaller scales. The former is modeled by a homogeneous and isotropic distribution of energy density; the latter issue is addressed in terms of gravitational instability which will amplify the small perturbations in the energy density, leading to the formation of structures like galaxies. In such an approach, the expansion of the background universe is described by the metric (We shall use units with with c = 1 throughout, unless otherwise specified):

(1)

with S_k() = (sin, , sinh) for the three values of the label k = (1,0,-1). The function a(t) is governed by the equations:

(2)

The first one relates expansion rate of the universe to the energy density and k = 0, ± 1 is a parameter which characterizes the spatial curvature of the universe. The second equation, when coupled with the equation of state p = p() which relates the pressure p to the energy density, determines the evolution of energy density = (a) in terms of the expansion factor of the universe. In particular if p = w with (at least, approximately) constant w then, a^-3(1+w) and (if we further assume k = 0, which is strongly favoured by observations) the first equation in Eq.(2) gives a t^2/[3(1+w)]. We will also often use the redshift z(t), defined as (1 + z) = a₀ / a(t) where the subscript zero denotes quantities evaluated at the present moment. in a k=0 universe, we can set a₀ = 1 by rescaling the spatial coordinates.

It is convenient to measure the energy densities of different components in terms of a critical energy density (_c) required to make k = 0 at the present epoch. (Of course, since k is a constant, it will remain zero at all epochs if it is zero at any given moment of time.) From Eq.(2), it is clear that _c = 3H₀² / 8 G where H₀ ( 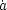/ a)₀ - called the Hubble constant - is the rate of expansion of the universe at present. Numerically

			(3)

The variables _{i i} / _c will give the fractional contribution of different components of the universe (i denoting baryons, dark matter, radiation, etc.) to the critical density. Observations then lead to the following results:

(1) Our universe has 0.98 _tot 1.08. The value of _tot can be determined from the angular anisotropy spectrum of the cosmic microwave background radiation (CMBR; see Section 6) and these observations (combined with the reasonable assumption that h > 0.5) show [1] that we live in a universe with critical density, so that k = 0.

(2) Observations of primordial deuterium produced in big bang nucleosynthesis (which took place when the universe was about few minutes in age) as well as the CMBR observations show [2] that the total amount of baryons in the universe contributes about _B = (0.024 ± 0.0012) h^-2. Given the independent observations [3] which fix h = 0.72 ± 0.07, we conclude that _B 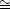0.04-0.06. These observations take into account all baryons which exist in the universe today irrespective of whether they are luminous or not. Combined with previous item we conclude that most of the universe is non-baryonic.

(3) Host of observations related to large scale structure and dynamics (rotation curves of galaxies, estimate of cluster masses, gravitational lensing, galaxy surveys ..) all suggest [4] that the universe is populated by a non-luminous component of matter (dark matter; DM hereafter) made of weakly interacting massive particles which does cluster at galactic scales. 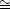This component contributes about _DM 0.20-0.35 and has the simple equation of state p_DM 0. The second equation in Eq.(2), then gives _DM a^-3 as the universe expands which arises from the evolution of number density of particles: = nmc² n a^-3.

(4) Combining the last observation with the first we conclude that there must be (at least) one more component to the energy density of the universe contributing about 70% of critical density. Early analysis of several observations [5] indicated that this component is unclustered and has negative pressure. This is confirmed dramatically by the supernova observations (see Ref. [6]; for a critical look at the current data, see Ref. [7]). 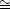The observations suggest that the missing component has w = p / -0.78 and contributes _DE 0.60-0.75. The simplest choice for such dark energy with negative pressure is the cosmological constant which is a term that can be added to Einstein's equations. This term acts like a fluid with an equation of state p_DE = -_DE; the second equation in Eq.(2), then gives _DE = constant as universe expands.

(5) The universe also contains radiation contributing an energy density _R h² = 2.56× 10^-5 today most of which is due to photons in the CMBR. The equation of state is p_R = (1/3) _R; the second equation in Eq.(2), then gives _R a^-4. Combining it with the result _R T⁴ for thermal radiation, it follows that T a^-1. Radiation is dynamically irrelevant today but since (_R / _DM) a^-1 it would have been the dominant component when the universe was smaller by a factor larger than _DM / _R 4× 10⁴ _DM h².

(6) Taking all the above observations together, we conclude that our universe has (approximately) _DE 0.7, _DM 0.26, _B 0.04, _R 5× 10^-5. All known observations are consistent with such an - admittedly weird - composition for the universe.

Using _NR a^-3, _R a^-4 and _DE = constant we can write Eq.(2) in a convenient dimensionless form as

(4)

where = H₀ t, a = a₀ q(), _NR = _B + _DM and

(5)

This equation has the structure of the first integral for motion of a particle with energy E in a potential V(q). For models with = _NR + _DE = 1, we can take E = 0 so that (dq / d) = (V(q))^1/2. Based on the observed composition of the universe, we can identify three distinct phases in the evolution of the universe when the temperature is less than about 100 GeV. At high redshifts (small q) the universe is radiation dominated and Img src="../../New_Gifs/qdot.gif" alt="dot{q}"> is independent of the other cosmological parameters. Then Eq.(4) can be easily integrated to give a(t) t^1/2 and the temperature of the universe decreases as T t^-1/2. As the universe expands, a time will come when (t = t_eq, a = a_eq and z = z_eq, say) the matter energy density will be comparable to radiation energy density. For the parameters described above, (1 + z_eq) = _NR / _R 4× 10⁴ _DM h². At lower redshifts, matter will dominate over radiation and we will have a t^2/3 until fairly late when the dark energy density will dominate over non relativistic matter. This occurs at a redshift of z_DE where (1 + z_DE) = (_DE / _NR)^1/3. For _DE 0.7, _NR 0.3, this occurs at z_DE 0.33. In this phase, the velocity changes from being a decreasing function to an increasing function leading to an accelerating universe. In addition to these, we believe that the universe probably went through a rapidly expanding, inflationary, phase very early when T 10¹⁴ GeV; we will say more about this in Section 7. (For a textbook description of these and related issues, see e.g. Ref. [8].)

Before we conclude this section, we will briefly mention some key aspects of the background cosmology described by a Friedmann model.

(a) The metric in Eq.(1) can be rewritten using the expansion parameter a or the redshift z = (a₀ / a)^-1 -1 as the time coordinate in the form

(6)

This form clearly shows that the only dynamical content of the metric is encoded in the function H(a) = (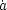 / a). An immediate consequence is that any observation which is capable of determining the geometry of the universe can only provide - at best - information about this function.

(b) Since cosmological observations usually use radiation received from distant sources, it is worth reviewing briefly the propagation of radiation in the universe. The radial light rays follow a trajectory given by

(7)

if the photon is emitted at r_em at the redshift z and received here today. Two other quantities closely related to r_em(z) are the luminosity distance, d_L, and the angular diameter distance d_A. If we receive a flux F from a source of luminosity L, then the luminosity distance is defined via the relation F L / 4 d_L²(z) . If an object of transverse length l subtends a small angle , the angular diameter distance is defined via (l = d_A). Simple calculation shows that:

(8)

(c) As an example of determining the spacetime geometry of the universe from observations, let us consider how one can determine a(t) from the observations of the luminosity distance. It is clear from the first equation in Eq. (8) that

(9)

where the last form is valid for a k = 0 universe. If we determine the form of d_L(z) from observations - which can be done if we can measure the flux F from a class of sources with known value for luminosity L - then we can use this relation to determine the evolutionary history of the universe and thus the dynamics.