


Before discussing numerical effects in cosmological disk galaxy formation simulations we should keep in mind that until the time of writing this field of research has been dominated by one numerical method, smoothed particle hydrodynamics (SPH) 35, 36, 37, 38, in which particles are tracers of average fluid quantities such as density, velocity and temperature associated with a finite volume of the fluid. The fluid is thus discretized by means of particles and the calculation of the fluid-dynamical equations is carried out in a Lagrangian fashion. The Euler equation for an inviscid ideal gas is solved rather than the more general Navier-Stokes equation. An artificial viscosity term is introduced in the hydrodynamical force equation and in the internal energy equation to compensate for some artifacts resulting from the discrete representation of the fluid equations, namely to avoid particle interpenetration and damp spurious oscillations in shocks 39. Although it is introduced for these good reasons, artificial viscosity also causes some unwanted numerical effects, such as damping the angular momentum of the fluid. One of the reasons behind the dominance of the SPH method in this field is that it couples naturally with the most efficient and accurate methods to compute gravitational forces in the fluid as well as in the collisionless dark matter component, the so called treecodes 37. Treecodes are an approximate but fast and accurate way of solving the N-Body problem 40. In treecodes gravitational forces between all particles, dark matter and baryons, are solved via a type of multipole expansion of the gravitational field which reduces to individual particle interactions only at short distances. Eulerian techniques that solve gravity and the fluid equations on a fixed or adaptive grid have been less used in this field of research because they have been generally slower and less accurate when it comes to compute gravity. However, the scenario is changing rapidly with the appearance of several fast, parallel adaptive mesh refinement codes (AMR) that are beginning to have an impact in studies of galaxy formation within a cosmological context 41, 42, 43. Restricting ourselves to the current particle-based methods, we will now briefly review the most important numerical artifacts that can severely affect the angular momentum content and structure of disks forming in the simulations. Many of the results that we will discuss in greater detail in this and in the following sections were obtained with the tree+SPH code GASOLINE 44 in simulations performed on large parallel supercomputers.
2.2. Numerical effects: two-body heating
One major problem of all particle-based simulations, both hydrodynamical and collisionless, is numerical two-body heating. Two-body heating is the spurious increase of kinetic or thermal energy of a particle representing gas, stars or dark matter due to a collision with another particle. Particles behave as gravitating point masses and therefore can undergo strong gravitational accelerations in close encounters with consequent large transfers of momentum. Such an effect is clearly an artifact of the discrete representation of a continuum by means of particles. For gas particles, such spurious large accelerations can be partially compensated by pressure or artificial viscosity that tend to deflect particles as they approach one another. In order to partially overcome this problem for all types of particles, gravity is decreased at small distances thanks to the introduction of gravitational softening 45. Softening the gravity field at scales of order the interparticle separation is consistent with the fact that individual particles should represent a fairly large sub-volume of the hydrodynamical fluid or collisionless continuum (e.g. the dark matter component) rather than real point-masses (in typical simulation dark matter and baryonic particles can indeed weight 106 - 107 solar masses) However, in cosmological simulations of the CDM model dark matter particles are typically much heavier than gas and star particles because dark matter accounts for most of the mass. As a result massive dark matter particles can transfer significant kinetic energy during gravitational encounters with other particles despite the presence of gravitational softening.
This spurious transfer of energy in two-body encounters increases the kinetic energy in random motions because any component of the velocity can be boosted as a result of a given encounter. Numerical experiments have shown that rotationally supported, thin stellar disks can be gradually degraded into a thick spheroidal distribution because the random velocity of the baryonic particles becomes increasingly more important compared to ordered rotation 46. If two-body heating is moderate and a recognizable disk component survives the angular momentum of the disk along the original axis of rotation still decreases as a result of the randomization of velocity vectors 46. Hence two-body heating induces artificial angular momentum loss. Gas particles suffer an increase of temperature as a result of two-body heating 47. This affects the radiative cooling efficiency of the gas because the cooling rate is a function of temperature 47. The increase of temperature occurs because the kinetic energy gained in two-body collisions is thermalized by artificial viscous dissipation. The only way to reduce these effects is to reduce the graininess of the mass distribution, which is only achieved by increasing the number of particles used in the simulation. This of course calls for more computing power.
The reduction of spurious effects induced by two-body heating with increasing resolution has been tested systematically by means of toy-models that represent an isolated, already assembled galaxy 34, 46. This type of models is idealized but allows to gain insight into the phenomenology of the much more complex cosmological simulations where many interacting objects are simultaneously modeled. Such studies have indicated that > 105 particles are required in the dark matter of a single galaxy to keep the spurious kinetic energy increase to levels < 10 %. In typical cosmological simulations many galaxies are followed at the same time and the latter becomes a tough resolution requirement.
2.3. Numerical loss of angular momentum in the baryonic component
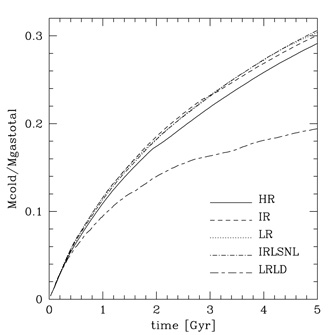
When the resolution in the dark matter component is high enough to overcome two-body heating there are other numerical artifacts that can affect the formation and evolution of galaxies in the simulations, including the size and angular momentum of the disk. These are related to how well the gas component is resolved, namely on the number of gas particles. and is once more best studied using idealized numerical experiments with isolated galaxy models. These experiments show that gas particles can lose angular momentum as they collapse within the dark matter halo before they settle into a centrifugally supported orbit and join the disk 49, 50, 48. Spurious angular momentum loss can happen for various reasons; (1) artificial viscosity; (2) the interaction between particles with significant temperature difference. The disk edge, where cold particles already belonging to the disk are close to hotter particles still in process of cooling and collapsing from the outer part of the halo. The cold particles suffer an artificial drag from the hot particles as a result of an erroneous estimate of the pressure gradient performed by the standard SPH method 51, 52, 50, and shrink to a smaller radius; (3) the disk can be quite asymmetric at low gas resolution and because of this suffers a strong gravitational torque from the surrounding halo, which then extracts its angular momentum. This latter effect is very subtle because disks might become asymmetric as a result of internal, physical evolution of the mass distribution. Some observed galaxies indeed have asymmetries, such as bars and oval-shaped disks. Nevertheless the asymmetry seen in the low-res simulations is artificial because it partially disappears as the resolution is increased (Figure 4 shows that the disk becomes rounder as the resolution is increased). The overall result of numerical experiments at varying resolution is that, while the amount of collapsed mass in the disk converges rapidly with resolution (Figure 5), angular momentum loss becomes negligible only when the number of gas particles in an individual galaxy model approaches 106 (Figure 5).
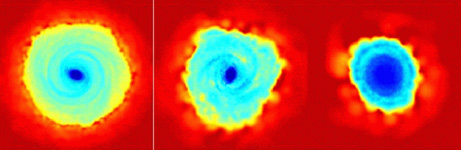 |
Figure 4. Disk size as a function of mass resolution in numerical simulations of disk formation in an isolated CDM halo 48 (2007 Blackwell Publishing Ltd). The three panels show density maps of gas in a slice through the centre of the gaseous galactic disk after 5 Gyr; the gas mass resolution decreases from the left to the right by about a factor 8 each snapshot (the maximum resolution is 1 million gas particles). The box side length is 20 kpc for every panel. At all resolutions disks show asymmetries such as central bar-like structures and spiral arms. The bar, however, is a strong and long-lived feature only for sufficiently high spatial resolution (set by the gravitational softening) 48. |
 |
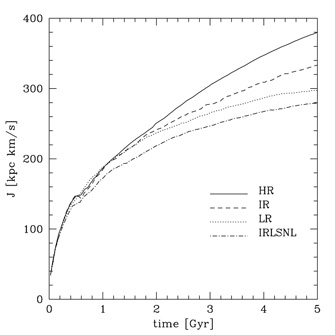 |
Figure 5. Top: growth of the disk mass (expressed relative to the total gas mass within the dark halo) as a function of resolution 48 (2007 Blackwell Publishing Ltd). Bottom: Evolution of the specific angular momentum in the disk as function of resolution 48. The resolution of the simulations is increasing from LRLD (3 × 104 gas matter particles and 2.5 × 103 dark matter particles) to LR (3 × 104 dark matter and gas particles), IR (9 × 104 dark matter and gas particles) and HR (5 × 105 gas matter particles and 106 dark matter particles); IRLSNL differs from the other runs in the prescription of artificial viscosity. See Table 1 in 48 for details on the simulations. |
Once the disk has formed, artificial viscosity can continue to degrade angular momentum, especially near the center of disks where velocity gradients become very steep and the relative motion of the particles is poorly modeled. Indeed without efficient heating by supernovae feedback or by other mechanisms, the inner disk always becomes very dense and loses angular momentum, even with millions of SPH particles 48. Gravitational instability in the gaseous or stellar component of the disk (this arises when the disk becomes quite massive as more gas is accreted from the halo) can also generate transport of angular momentum via non-axisymmetric structures such as bars and spiral arms 2 (see Figure 4), which are ubiquitous in observed galaxies 53. Bars can transport angular momentum outward very efficiently 2. As a result they can flatten the disk density profile by pushing out the gas and/or the stars just outside the bar region 54. This affects the final disk size, with a tendency to increase it relative to the case where no bar forms. Unfortunately, even this kind of angular momentum transport depends on resolution; this time the spatial resolution of self-gravity, which is set by the gravitational softening length, has to be high enough to capture the wavelength of the non-axisymmetric modes of the density field responsible for bar formation 48.
2.4. Resolution issues in cosmological disk formation simulations
Cosmological simulations of disk formation follow the nonlinear development of structure in a fairly large volume, of order 50 Mpc3, which is much larger than the volume occupied by an individual galaxy-sized halo. The reason of this apparent redundancy is that the large scale tidal field needs to be included in order to properly compute the tidal torques that generate the angular momentum of the galaxy-sized halos. The larger volume implies more mass to sample and therefore implies that the resolution requirements indicated in the previous section will be much harder to meet. To overcome this problem a technique has been developed, and constantly improved in the last decade or so, to increase the resolution in a selected region within a large cosmological volume. This way the halo of a single galaxy can be resolved by up to a million dark matter and gas particles 34, 55, 56, 57. This is the so-called renormalization technique (Figure 6). In this technique, the computational volume includes regions with varying mass and spatial resolution; the masses of the particles, and therefore their mean separation, increase with the distance from the selected object, for example a single galaxy-sized halo. This way most of the particles are placed in the region of interest, optimizing the use of computer time. Thanks to the latter technique, more evidence has been gathered on the effect of resolution directly in cosmological simulations. The analysis of the renormalized simulations confirms that disk size and angular momentum increases as the resolution of both the dark matter and baryonic component is increased. Simulations with hundreds of thousands baryonic and dark matter particles do produce stellar disks whose size is indeed comparable with that of real galaxies 58, 59, 34, 55, 56, 60. The most recent and highest resolution (> 106 particles per galaxy) of these simulations even produce high angular momentum gas disks that extend well beyond the stellar component, as observed in most spiral galaxies (Figure 8). However, a spheroidal bulge component always forms at the center of the galaxy (Figure 7, 8, 9). The bulge comprises low angular momentum material brought by several mergers early in the assembly history of the system 34, 58. It is too dense and massive compared to that seen in typical disk galaxies. On the other end, such a dense and massive bulge is not very different from that of at least some galaxies, such as the closest nearby spiral galaxy, Andromeda. It is conceivable that the high density and large mass of the bulge might be at least partially caused by artificial loss of angular momentum during the early stages of galaxy assembly. In fact, even in the highest resolution renormalized simulations the progenitors of the final galaxy have only a few thousand particles when the bulge forms, ten billion years before the present epoch 55, a resolution well below that recommended by numerical experiments with isolated galaxies 48.
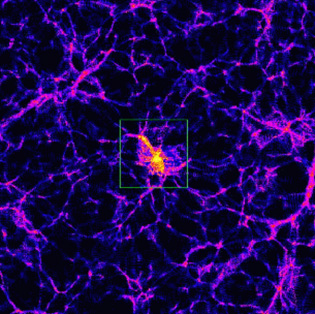 |
Figure 6. Example of renormalized cosmological volume 34. The spatial distribution of dark matter particles during the simulation is shown, color coded in density. The region marked in green has been resampled at higher resolution compared to the rest of the volume (whose total size is 100 Mpc) to follow the formation of a galaxy-sized object inside it. |
 |
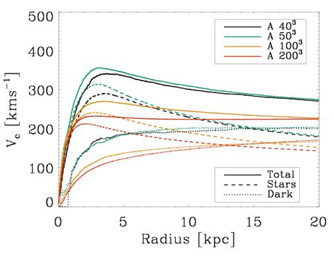 |
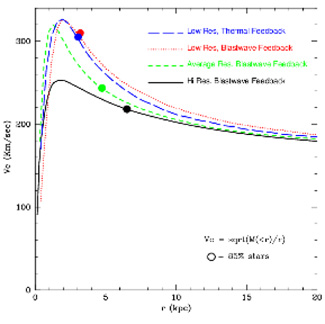
Figure 7. Top: Rotation curve in cosmological disk galaxy as a function of resolution and feedback model 55. See section 3.4 for a description of feedback models. The resolution of the simulated galaxy varies from ~ 104 (low-res) to ~ 105 (average-res) to ~ 106 SPH and dark matter particles within the virial radius. The open dots mark the radius at which 85% of the stars are located. Bottom: Rotation curves of massive galaxies formed in cosmological simulations for varying resolution 61 (reproduced by permission of the AAS, 2007). The cosmological box is simulated with four different numerical resolutions: 403, 513, 1003, and 2003 SPH particles and collisionless dark matter particles. Note how the rotation curves become increasingly flat as the resolution increases. In both cases the rotation curve is calculated including all components, dark matter, stars and gas, in the computation of the mass. |
 |
Figure 8. Snapshot of a high-resolution galaxy formation simulation at a time close to the present epoch (the resolution is comparable to the highest resolution runs published by our group 55). The gas is shown in green and the stars are coloured differently based on when they formed. It can be seen that most of the stars are concentrated in the central region while gas is a arranged in an extended disk component with radius about 50 kpc (the whole image is about 200 kpc on a side). |
 |
Figure 9. Disk size and morphology in cosmological simulations of a Milky-Way sized galaxy 55 with varying resolution, performed with the blast-wave feedback sub-grid model described in section 3 and section 4. Mock observations of the simulated galaxies, obtained using the software SUNRISE 137, are shown in optical wavelengths I-band (top panels) corresponding to a particular band seen by the telescope of the Sloan Digital Sky Survey (SDSS)) and in ultraviolet bands (as seen by the GALEX ultraviolet satellite). |
It is encouraging that the central concentration of mass, like the disk size, also decreases as the resolution is increased. This can be quantified by measuring the rotational velocity of the baryonic material as a function of radius, hence deriving the "rotation curves" that observational astronomers use to probe the dynamics of real galaxies (Figure 7). The degree of rotation is determined by the depth of the gravitational potential well; assuming spherical symmetry, and that all the kinetic energy of the baryons is in rotational form, the rotational velocity at any given radius in the galaxy will be given by Vrot = (GM / R)1/2 (M is the mass, R is the radius and G is the gravitational constant). Vrot tends to increase towards the center if a massive central bulge component is present. Likewise, it becomes flatter near the center as the mass of the central bulge diminishes. Figure 7 shows the rotation curves obtained by two different groups using two different numerical codes 55, 61. It demonstrates that the rotational velocity decreases with increasing mass resolution, as expected if the spurious angular momentum loss of the baryonic material decreases with increasing resolution. From the Figure it appears that the rotation curve is also affected by other factors, namely the presence or absence of heating by supernovae feedback that will be discussed in the next section. Stronger heating will in fact counterbalance gas cooling; it will thus reduce the amount of cold gas that collapses to the center of the progenitor halos forming the stars that will be later incorporated into the bulge.