2. GALAXY-SCALED STAR FORMATION AND ISM DYNAMICS - BASIC FACTS

2.1. Disk stability and star formation

Star formation on large scales proceeds by gravitational instabilities, which create dense clouds in which the gas cools more rapidly, and continue to fragment and collapse into start through gravitational (and thermal) instabilities.

The simplest prescriptions on whether a large (kpc-size) region of a galaxy will form stars and at which rate can be obtained by studying its gravitational stability. For a gas medium of size L, density and velocity dispersion ¹ , pressure forces on the surface vary as L², and necessarily overcome self-gravity, which scales as the mass, hence as L³. For large-enough scale, gravitational forces eventually dominate and large-enough regions are gravitationally unstable (Fig. 1).

Figure 1. An homogeneous region of volume density is unstable if its size is at least the Jeans length, which enables gravity to overcome pressure forces from the internal velocity dispersion . If the region is embedded in a rotation disk, the collapse can occur only if the size is small enough compared to the imposed shear ; the Q < 1 Toomre criterium indicates that the combination of both constraints can be satisfied.

The critical scale, which is also the most unstable one (the fastest growing mode) is the Jeans scale, set by:

(1)

If gravitational collapse occurs, gas becomes denser, so the cooling time drops and the gas effectively gets colder, making pressure forces more and more negligible compared to gravity. It is hence realistic to consider the collapse of gas clouds as a "free fall" process, i.e. not regulated by pressure forces, at least until the scales of magnetic pressure in dense cores are reached, or until star formation has taken place and young stars start to heat and ionize the gas. The gravitational free-fall time is given by:

(2)

At fixed density in an infinitely large system and without external rotation, a large-enough region will always be unstable. But the question to decide on dense gas cloud formation and subsequent star formation is whether sufficient mass can be gathered over a size not larger than the entire galaxy, and even over a size not larger than the disk scale height (above which the mass stops growing as L³). Thus a given region of a galaxy may be dense enough or not to be gravitationally unstable and form dense gas and stars.

Another aspect is the stabilization by rotation and shear in galactic disks. Too large regions will be torn apart by the shear faster than they tend too collapse, namely faster than the gravitational free-fall time. This process stabilizes regions that are large enough to undergo large differential rotation. This is formalized by the Toomre (1964) parameter:

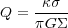(3)

where is the surface density of the disk, is the so-called epicyclic frequency, without a factor 2 from the angular speed in galactic disks with standard rotation curves (3.36 replaces in the definition of Q for a collisionless fluid, i.e. a stellar disk).

Q > 1 means that any scale is stabilized either by pressure or rotation - scales smaller than the Jeans length are stabilized by the gas pressure, and the Jeans length is already large enough to be stabilized by rotation.

Regions with Q < 1 can collapse, fragment, form cold gas clouds and star-forming cores therein, and this collapse should take a gravitational free-fall time.

2.2. The heterogeneous and turbulent ISM

The simple description above could give a simple model to describe star formation in galaxies in theory and in simulations. Only regions where Q < 1 can form stars, and then a certain fraction of gas is converted into stars within one or a few free-fall times, the involved fraction being much smaller than one (typically a few percent) because the formation of the first stars will heat the surrounding gas and regulate the formation of the next stars (although young stars can also remotely trigger the formation of other stars (e.g., Elmegreen & Lada 1977)).

However, the involved critical scale in this "Q < 1 approach", the Jeans length or Toomre length (this two scalelengths are of the same order of value), is of the order of 100-1000 pc for normal spiral galaxies such as the Milky Way. If we consider a portion of the ISM of a few hundreds of pc, we will find warm atomic gas at densities of a few atoms per cubic centimeter and temperatures of a few 10³ K, colder and denser atomic gas, molecular gas with densities of 10³ to 10⁶ cm^-3, ionized gas at ~ 1 cm^-3 and a few 10⁴ K, etc. It is then impossible to define a typical density and velocity dispersion (or sound speed) in the ISM on the scales that are relevant to measure a Toomre parameter, making this theory impossible to apply to real galaxies.

The only framework in which the basic theory of gravitational instability in disks can be directly applied are maybe the resolution-limited SPH simulations that are a plenty in the literature since almost two decades. Most of these simulations (except a few recent ones) do not resolve an heterogeneous ISM, the only density fluctuations arising on scales of a kpc and above. There a relevant Toomre parameter can be measured and applied as a star formation criterium. But at the same time, this simple fact means that the involved ISM model has a quite limited realism.

If we consider the various phases of the ISM in the Galaxy, up to one third of the volume may be filled with warm and hot gas above 10⁴ K, but at least two thirds of the mass (and 100% of the mass involved in dense gas cloud formation and star formation) are in denser and colder phases with temperatures between, say, 10 K and 10^3-4 K. The sound speed in atomic hydrogen at 10⁴ K is about 10 km s^-1, thus the star-forming phases of the ISM have a sound speed of the order of a km s^-1 (0.1 to 10 km s^-1).

Observed linewidths of the gas in spiral galaxies are at least a few km s¹, they can reach 50 or 100 km s¹ in interacting galaxies (see details and references later), starbursting galaxies, and in gas-rich galaxies at high redshift. This is observed even on scales much smaller than the rotational velocity gradient in disk galaxies, which shows that supersonic non-circular motions are ubiquitous in the ISM of galaxies.

Interestingly, observations of the density power spectrum of nearby galaxies suggest that these random motions follow a cascade process from a large injection scale down to dissipation on small scales (Block et al. 2010, Dutta et al. 2009, Elmegreen et al. 1993). The spectral signature of this cascade is just as expected from turbulence experiments (Petersen et al. 2007). This indicates that the non-circular motions in the ISM can be named turbulence. A key property of this ISM turbulence is that it is supersonic, since the involved motions largely exceed the sound speed. Mach numbers of a few for the cold star-forming ISM phases are typical for spiral galaxies, they may frequently reach ~ 10 in starbursts, and high-redshift galaxies (e.g., Förster Schreiber et al. 2009).

2.3. Star formation in the turbulent ISM

The connection between ISM turbulence, dense gas phases and star formation is best understood by examining the point distribution function of the local gas density (density PDF). In its mass-weighted (resp. volume-weighted) version, the density PDF represents the mass (volume) fraction of the ISM in bins of density. We here use mass-weighted versions.

In an system at equilibrium (e.g. isolated disk galaxy), supersonic turbulence generates a log-normal density PDF (Wada et al. 2002) (see Fig. 2). Only small mass fractions of the whole ISM are at found number densities below ~ 1 cm^-3 or in very high density regions above, say, 10⁴ cm^-3, most mass being at ten to a few hundreds of atoms per cm³ (typically observed as HI or CO-traced molecular gas). The width of the log-normal PDF depends on various factors, but the main dependence is on the turbulent Mach number, with the PDF width increasing when the Mach number increases (see Krumholz & Thompson 2007 for details). A more turbulent ISM will have a larger spread in its density PDF, because the turbulent flows will sometimes diverge and create low-density holes, and sometimes converge (or even shock) into very dense structures that can further collapse gravitationally. Note that log-normal density PDFs are observed, at least at the scale of molecular complexes (Lombardi et al. 2010).

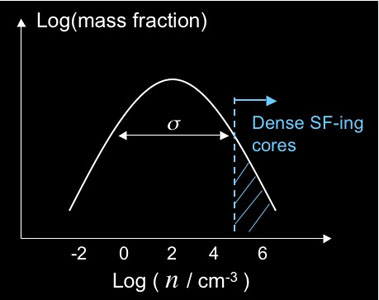Figure 2. This figure illustrates a density PDF, with a log-normal shape and typical value for the galactic ISM. The intrinsic spread of the PDF increases with the Mach number of the non-circular (turbulent) motions in the ISM (Wada et al. 2002, Krumholz & Thompson 2007). The log-normal shape exist is the turbulence is (1) isothermal (but in the real non-isothermal ISM the high Mach numbers keep the PDF quasi log-normal anyways) in a steady-state (i.e. for an isolated self-regulated disk but not necessarily for a suddenly disturbed system in an interaction).

The density PDF is a useful tool to describe the star-forming activity of a galaxy at a given gas content. For a simplified description, one can consider that star formation takes place only in the densest gas phases (i. e. above some density threshold), and that in these dense regions the local star formation rate follows, for instance, a fixed efficiency per free-fall time: _SFR = _{ff gas} / t_{ff gas}^1.5 (see detailed theory in Elmegreen 2002 and Krumholz & Thompson 2007). Even if the local rate of star formation follows a different behavior than this purely density-dependent model (which is physically motivated by the gravitational collapse timescale), then the first step remains that star formation proceeds only in the densest gas phases once dense-enough clouds have formed. The weight of this "star-forming phase" is given by the high-density tail of the PDF. Hence, the fraction of dense gas along the density PDF is a key parameter for the global star formation activity of any given galaxy. The density PDF will thus be a major tool to understand starburst activity in galaxy mergers.

¹ This velocity dispersion can be thermal (microscopic) and/or turbulent (macroscopic). Back.