6. James Webb Space Telescope SIGNATURE

The upcoming JWST, together with the next-generation of 30-40m extremely large ground-based telescopes, will revolutionize our picture of the high-redshift Universe. Among the main JWST science goals is the detection of light from the first galaxies, and more generally to elucidate early structure formation at the end of the cosmic dark ages (Gardner et al. 2006). The key predictions concern the expected flux and number densities of the first galaxies, enabling us to assess their detectability with the instruments aboard the JWST (e.g., Salvaterra, Ferrara & Dayal 2011). In carrying out these predictions, a number of challenges still need to be overcome prior to its projected launch in ~ 2015 (see the contributions in Whalen, Bromm & Yoshida 2010). We begin by briefly summarizing the JWST capabilities. A more detailed discussion is made by Gardner et al. (2006) and Stiavelli (2009).

6.1. JWST Instruments and Sensitivities

The observatory will carry out deep field imaging with the Near-Infrared Camera (NIRCam) and the Mid-Infrared Instrument (MIRI), as well as medium-resolution spectroscopy with the Near-Infrared Spectrograph (NIRSpec) and MIRI. NIRCam will have a field of view of 2.2' × 4.4', and an angular resolution of ~ 0.03"-0.06" in the range of observed wavelengths _obs = 0.6-5 µm. The multi-object spectrograph NIRSpec will carry out medium resolution (R ~ 100 - 3000) spectroscopy of up to ~ 100 objects simultaneously within a field of view of 3.4' × 3.4', where R _obs / _obs is the spectral resolution. NIRSpec will operate in the same wavelength range as NIRCam but at lower angular resolution (~ 0.1"). Finally, MIRI will complement NIRCam and NIRSpec by providing imaging, low and medium resolution spectroscopy within the range of observed wavelengths _obs = 5-28.8 µm and fields of view and angular resolutions of, respectively, ~ 2' × 2' and ~ 0.1" - 0.6".

In quoting sensitivities, or flux limits f_lim, for the JWST instruments, a signal-to-noise ratio of S / N = 10 and exposure times of t_exp = 10⁴ s are often assumed. These baseline sensitivities are summarized in table 10 by Gardner et al. (2006). Ultra-deep exposures with JWST may extend to t_exp = 10⁶ s, which is comparable to the HUDF observations, with flux limits being rescaled according to: f_lim 1 / (t_exp)^1/2. Panagia (2005) contains a useful graphical representation of the JWST sensitivities, nicely emphasizing the jump in going from the near-IR to the mid-IR. Approximate numbers, for the deep exposures, are f_lim ~ 1 nJy for NIRCam, and 10 times higher for the MIRI imager; spectroscopic limits are typically two orders of magnitude higher than the imaging ones. It is customary to also work with the AB magnitude system (Oke 1974; Oke & Gunn 1983). Specific fluxes, f, can then be expressed as

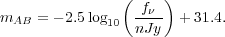(4)

Even for exposure times as long as 10⁶ s, JWST will not have sufficient sensitivity to detect sources with stellar masses below ~ 10⁵ - 10⁶ M. In particular, JWST will not be able to directly detect individual Pop III stars at high redshifts (Bromm, Kudritzki & Loeb 2001). Therefore, starbursts in the first galaxies are the primary targets for JWST. As was already recognized by Partridge & Peebles (1967), the first galaxies were likely brightest in the recombination lines of hydrogen and helium (Schaerer 2002, 2003; Johnson et al. 2009; Pawlik, Milosavljevic & Bromm 2011), in particular the Lyman-, H and He II 1640 Å nebular emission lines (see Figure 11).

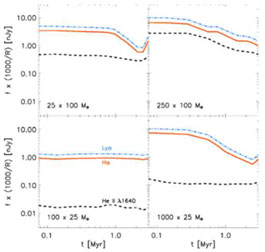Figure 11. Emission line fluxes in the first galaxies. Shown are predictions for observable recombination line fluxes as a function of time. The source is an atomic cooling halo at z 12.5. The lines are: Ly (dot-dashed blue), H (solid red) and He II 1640 Å (dashed black). The fluxes are normalized to a spectral resolution of R = 1000. The Ly flux is an upper limit, due to the possibly severe attenuation by the surrounding, still largely neutral, IGM. Adopted from Johnson et al. (2009).

6.2. Observing High-redshift Sources

It is convenient to review the basic relations that relate observed to intrinsic quantities, as employed in observational cosmology (see also Loeb 2010).

We begin by translating intrinsic line and UV continuum luminosities into observed fluxes. The specific flux from a spatially unresolved object emitted in a spectrally unresolved line with rest-frame wavelength _em and intrinsic line luminosity L_em is given by Oh (1999) and Johnson et al. (2009):

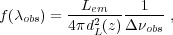(5)

where _obs = c / (_obs R), and _obs = (1 + z) _em. A convenient approximation for the luminosity distance is: d_L ~ 100 [(1 + z) / 10] Gpc. For typical parameters, one then has:

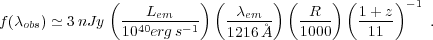Let us now discuss whether the lines, expected to be emitted by the first galaxies, are indeed spatially and spectrally unresolved. The assumption of spectrally unresolved lines is excellent for both H and He II 1640 Å , whose line widths / < 10^-4 (T / 10⁴ K)^1/2 are set by thermal Doppler broadening at temperature T < 10⁴ K (Oh 1999). At redshifts z 10 a transverse physical scale l corresponds to an observed angle = l / d_A ~ 0.1" (l / 0.5 kpc) [(1 + z) / 10], where d_A = (1 + z)^-2 d_L is the angular diameter distance. If the recombination lines originate in the ionized nebulae in the central regions of the first galaxies at r < 0.1 r_vir, the assumption that the emitting regions are spatially unresolved is also good for both the H and the He II 1640 Å lines, and it applies equally well to the UV continuum. Here, we use a virial radius of r_vir ~ 1 kpc to describe the overall size of the first galaxies, which is typical for the systems discussed in Section 4. In contrast, the Lyman- line undergoes resonant scattering (Harrington 1973; Neufeld 1990), and hence will originate from within a spatially extended region with typical angular size ~ 15" (Loeb & Rybicki 1999), and be heavily damped due to absorption by intergalactic neutral hydrogen (Santos 2004; but see Dijkstra & Wyithe 2010). Indeed, Lyman- radiation from galaxies at redshifts z 10 may be severely attenuated because the bulk of the Universe was likely still substantially neutral at these redshifts.

A complementary way to quantify the strength of an observed line uses (redshifted) equivalent widths, which can easily be translated into the corresponding rest-frame values (e.g., Johnson et al. 2009): W₀ = f_line / f, where we have used the intrinsic line and neigboring (specific) UV continuum fluxes. Predicted equivalent widths for the first galaxies can reach W₀ 100 Å for He II 1640 Å , and W₀ 100 Å for the hydrogen lines (Johnson et al. 2009).

6.3. Modelling Star Formation in the First Galaxies

Making predictions for the luminosities and colors of the first galaxies sensitively depends on what one assumes for the stellar populations and star formation model (e.g., Schaerer 2002, 2003; Johnson et al. 2009; Raiter, Schaerer & Fosbury 2010; Pawlik, Milosavljevic & Bromm 2011; Salvaterra, Ferrara & Dayal 2011). One possibility is that stars form in a single instantaneous burst with total stellar mass

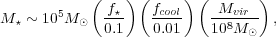(6)

where f_cool is a conversion factor that determines the amount of gas mass available for starbursts inside halos with virial masses M_vir, and f_* is the star-formation efficiency, i.e., the fraction of the available gas mass that is turned into stars. The parameters are normalized to what we have learned from simulating the formation of atomic cooling halos (see Section 4). Specifically, the choice of f_cool = 0.01 reflects the rapid accretion (t_acc < 10 Myr) of large gas masses (M_gas > 10⁶ M) into the central regions, as seen in the simulations. The star formation efficiency may be quite high in a burst mode, f_* = 0.1, where accretion times are comparable to the typical lifetimes ( ~ 10 Myr) of massive stars. Star formation may then not be affected by strong feedback capable of halting the collapse of the accreting gas. Another possibility is that stars form continuously. Atomic cooling halos, with their masses of ~ 10⁸ M, may have potential wells that are still too shallow to enable continuous star formation despite the disruptive effects of stellar feedback (see Section 4). Galaxies with total (virial) masses of 10⁹ M, however, may have been able to sustain such a near-continuous mode (Wise & Cen 2009). One can approximately include the effect of stellar feedback by employing a lower efficiency, f_* = 0.01, than appropriate for a starburst. The implied star formation rates _*(z) ~ 0.1 M yr^-1 are consistent with those found in recent low-mass galaxy formation simulations (Wise & Cen 2009; Razoumov & Sommer-Larsen 2010).

The luminosities of the first galaxies critically depend on the metallicities, ages, and IMF of their stellar populations. Some of the lowest-mass galaxies may still contain zero-metallicity gas. The resulting stars may form with a top-heavy IMF, biased towards high mass (M_* ~ 100 M) stars, as is expected to be the case for the first, metal-free generation of stars which form via molecular hydrogen cooling (Bromm et al. 2009). The IMF of metal-free stars is, however, still subject to large theoretical uncertainties. Stars forming out of gas with elevated electron fractions, such as produced behind structure formation or SN shocks, or as present in ionized regions, could have characteristic masses substantially less than < 100 M (see Section 4). The assumption of metal-free star formation will be violated if previous episodes of star formation, for instance inside the progenitors of the assembling galaxy, enriched the gas with metals. Even a modest enrichment to critical metallicities as low as Z_crit < 10^-6 - 10^-3.5 Z may imply the transition from a top-heavy IMF to a normal IMF (Bromm et al. 2001; Santoro & Shull 2006; Schneider et al. 2006; Smith & Sigurdsson 2007). Note that even a few SN explosions may already be sufficient to enrich low-mass ( ~ 10⁸ M) galaxies to metallicities Z > Z_crit (Wise & Abel 2008; Karlsson, Johnson & Bromm 2008; Greif et al. 2010; Maio et al. 2011).

The luminosity in the He II 1640 Å line strongly depends on both the IMF and stellar metallicity, and also on the age of the galaxy, i.e., the time since the last major star-formation episode. At fixed IMF, a change from low to zero metallicity implies an increase in the He II 1640 Å line luminosity by about three orders of magnitude for the first few million years after the starburst. This reflects the exceptionally hot atmospheres of zero-metallicity stars that render them into strong emitters of He II ionizing radiation (Tumlinson & Shull 2000; Bromm, Kudritzki & Loeb 2001; Schaerer 2003). For a top-heavy IMF, as advocated for primordial or very low-metallicity stars, the line luminosity is increased by another order of magnitude (see Figure 12). The large differences in luminosities offer the prospect of distinguishing observationally between stellar populations consisting of metal-free or metal-enriched stars, and of constraining their IMFs (Tumlinson & Shull 2000; Bromm, Kudritzki & Loeb 2001; Oh 2001; Johnson et al. 2009). JWST has the potential to constrain the properties of starbursts in galaxies with halo masses as low as ~ 10⁹ M, based on the simultaneous detection/non-detection of the H and He II 1640 Å lines (Pawlik, Milosavljevic & Bromm 2011). Indeed, only zero-metallicity starbursts with a top-heavy IMF can be detected in both H and He II 1640 Å , assuming exposure times 10⁶ s. Whether Lyman- can be detected as well will depend on the attenuation due to resonant scattering in the neutral IGM. Because of the greater sensitivity of NIRSpec compared to MIRI, Lyman- line emission is potentially easier to detect than H, and it hence remains a very powerful probe of galaxy formation at redshifts z 10, despite the large uncertainties caused by its resonant nature.

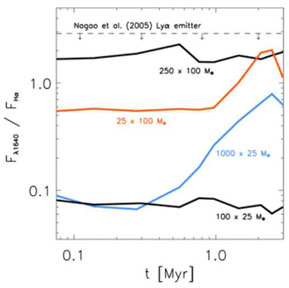Figure 12. IMF diagnostics in the first galaxies. Shown is the flux ratio in the He II 1640 Å to H recombination line as a function of time. The calculation assumes a central cluster of Pop III stars, all either with a mass of 25 M or 100 M for simplicity. The more massive Pop III stars lead to a ratio that is an order of magnitude larger, thus enabling to diagnose the nature of the stellar population. The dashed horizontal line corresponds to the upper limit for the strong Lyman- emitter SDF J132440.6+273607 at z 6.3 (Nagao et al. 2005). Evidently, this limit does not yet allow to distinguish between different populations. Adopted from Johnson et al. (2009).

6.4. Source Number Counts

The second key prediction concerns the number density of the first galaxies that JWST may observe. We can estimate the number of galaxies detectable with JWST, per unit solid angle, above redshift z as follows (e.g., Pawlik, Milosavljevic & Bromm 2011):

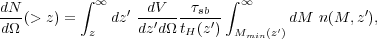(7)

where t_H(z) is the age of the Universe at z, and

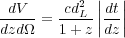the comoving volume element per unit solid angle and redshift. Here |dt / dz|^-1 (1 + z) H_{0 m}^1/2 (1 + z)^3/2, valid for high redshifts. n(M, z) is the comoving number density of galaxy host halos with mass M at redshift z, which can be derived from large cosmological simulations, or calculated with approximate analytical techniques. The latter approach often relies on variants of the Press-Schechter formalism (Press & Schechter 1974; for a recent review, see Zentner 2007). M_min(z) is the lowest (total or virial) halo mass capable of hosting a starburst that can be detected by the JWST. It depends on the stellar properties (metallicity and IMF), and on whether observations are made in, e.g., the H line, the He II 1640 Å line, or in the soft continuum. Typical values are M_min ~ 10⁸ - 10⁹ M for z 10 - 15 (Pawlik, Milosavljevic & Bromm 2011). Finally, _sb gives the duration of the starburst, which may vary from ~ 3 Myr for top-heavy Pop III stars, to ten times larger values for stars with normal IMF. In each case, this timescale measures the approximate time after which negative stellar feedback terminates the starburst. In Figure 13, we show results from a Press-Schechter based calculation (Pawlik, Milosavljevic & Bromm 2011), demonstrating that JWST may detect a few tens (for Z > 0 and normal IMF) up to a thousand (for Pop III with a top-heavy IMF) starbursts from z > 10 in its field-of-view of ~ 10 arcmin². This estimate is consistent with previous studies for similar assumptions about the conversion between halo and stellar mass (e.g., Haiman & Loeb 1997, 1998; Oh 1999; Trenti & Stiavelli 2008). Current calculations, however, still suffer from a number of uncertainties, such as whether Case B recombination theory is appropriate in the first galaxies (Schaerer 2003; Raiter, Schaerer & Fosbury 2010), the role of dust extinction (Trenti & Stiavelli 2006), the feedback-regulated star formation efficiency, and the escape fraction of ionizing radiation (Gnedin, Kravtsov & Chen 2008; Wise & Cen 2009; Johnson et al. 2009; Razoumov & Sommer-Larsen 2010; Yajima, Choi & Nagamine 2011).

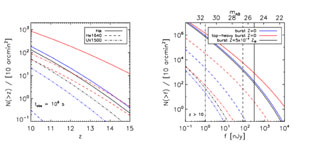Figure 13. JWST number counts of the first galaxies. The calculations assume texp = 106 s and S / N = 10. Left panel: Number of galaxies N(> z) with redshifts z > 10 hosting a starburst observable through the detection of H (solid lines), He II 1640 Å (dashed lines), or the soft UV continuum (dash-dotted lines). Colors denote different choices for stellar metallicity and IMF, as described in the inset of the righ-hand panel. Right panel: Number of galaxies N(> f) above z > 10 with observed fluxes > f. The vertical lines show the JWST flux limits for H (solid), He II 1640 Å (dashed), and the soft UV continuum (dash-dotted). JWST may detect a few tens (for Z > 0 and normal IMF) up to a thousand (for Pop III with a top-heavy IMF) starbursts from z > 10 in its field-of-view of ~ 10 arcmin2. Adopted from Pawlik, Milosavljevic & Bromm (2011).