Annu. Rev. Astron. Astrophys. 2005. 43: 769-826 Copyright © 2005 by Annual Reviews. All rights reserved

2. BASIC PHYSICS

2.1. Sources of Energy

The central question of what powers a GW dates back forty years to the discovery of the wind in M82. For reasons to be discussed in Section 5.1, remarkably few winds are unambiguously AGN (active galactic nucleus) or starburst driven. Hence, we now summarize the basic physics behind both kinds of energy sources.

2.1.1 STELLAR WINDS & SUPERNOVAE     Starburst winds are driven by the mechanical energy and momentum from stellar winds and supernovae (SNe). Models that synthesize the evolution of populations of massive stars have estimated the mass and energy returned from starbursts (e.g., Leitherer, Robert, & Drissen 1992; Leitherer & Heckman 1995; Leitherer et al. 1999, Starburst99). This technique combines stellar evolutionary models, atmospheric models, and empirical spectral libraries to determine the observable properties of the starbursting population. A wide parameter space is explored by varying the shape and mass limits of the stellar initial mass function (IMF), the metallicity, and the star formation rate (SFR) history (e.g., instantaneous burst or constant SFR). Stellar evolutionary models have reproduced successfully most properties of Wolf-Rayet (WR) stars, but overpredict WR mass-loss rates. In general, combined empirical results and theoretical predictions are used instead of model-derived mass-loss rates (Leitherer et al. 1992). For an instantaneous starburst, winds from OB stars dominate early on ( 3 Myr); next come WR stars with mass-loss rates ~ 10 times higher (~ 3 - 6 Myr); and finally, core-collapse Type II SNe dominate until ~ 40 Myr when the least massive (~ 8 M) ones explode.

Figures 107, 108, 113, and 114 from Leitherer et al. (1999) show the time evolution of the mass-loss rates and mechanical luminosities calculated using Starburst99 for two different starburst histories and various metallicities. In the solar-metallicity case where the mass-loss rate and mechanical luminosity are constant beyond ~ 40 Myr and scale with SFR,

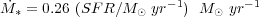(1)

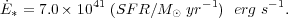(2)

Because 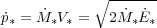, the rate of momentum injection from SNe and stellar winds into the environment can be calculated:

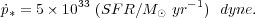(3)

In these expressions, the supernova rate 0.02 (SFR / 1 M yr^-1) yr^-1.

For comparison, the starburst's radiation pressure, L_bol / c, is

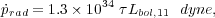(4)

where L_{bol, 11} is the bolometric luminosity of the starburst in units of 10¹¹ L and is the optical depth to radiation. In luminous IR galaxies where L_bol L_IR (8 - 1000 µm) 10¹¹ L and

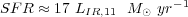(5)

(Kennicutt 1998), the radiation pressure in the optically thick case ( = 1) can be comparable to the pressure from the stellar ejecta.

In general, stellar winds are important only in young ( 10⁷ yr) starbursts that form many high-mass ( 60 M) stars in a metal-rich (Z > Z) environment. In any other situation, SN explosions dominate the energetics of the ISM. SN explosions usually dominate by the time GWs develop, but stellar winds may be important in superbubbles. Because the star formation activity in a starburst is highly correlated spatially, the ejecta from hot stars and SNe in the starburst region quickly interact through shocks, and mix with the surrounding gas to produce a cavity of hot, metal-enriched material. The thermalization efficiency is the percentage of the mechanical energy from the starburst that heats the gas. Unfortunately, as we show in Section 3 and Section 4, this quantity is poorly constrained by observations. Hydro simulations (Section 2.4) often assume it is 100%, i.e. none of the energy injected by the starburst is radiated away. In reality, this efficiency is set by the environment, particularly by the gas density, and may be 10% in the dense cores of powerful nuclear starbursts (e.g., Thornton et al. 1998; Silich, Tenorio-Tagle, & Muñoz-Tuñón 2003; Stevens & Hartwell 2003; Melioli & de Gouveia Dal Pino 2004). Conversely, large SN rates may increase the porosity of the ISM, and hence reduce radiative energy losses (e.g., Larson 1974; Cantó, Raga, & Rodriguez 2000; Wada & Norman 2001). Current data favor values 10% for the thermalization efficiency (see Section 4.5).

2.1.2 AGN     The ubiquity of supermassive BHs at the center of galaxies (e.g., Kormendy & Gebhardt 2001) suggests that BH activity may also power some galactic-scale outflows by accretion:

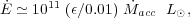(6)

where _acc is the mass accretion rate in M yr^-1 and , the energy conversion efficiency in rest mass units. The mass accretion rate ranges from 0.001 M yr^-1 for low-luminosity AGN, ~ 1 M yr^-1 for Seyfert galaxies, and ~ 100 M yr^-1 for quasars and powerful radio galaxies. The parameter depends on BH spin and the boundary conditions near the event horizon, and can reach 0.4 (e.g., Krolik 1999; Agol & Krolik 1999). Much of the energy released during accretion may be tapped to drive a GW; this can occur through several processes.

Radiative processes may be important in luminous AGN such as Seyfert galaxies and quasars. Radiation can push on the surrounding gas via electron scattering, scattering and absorption on dust grains, photoionization, or scattering in atomic resonance lines. The last one is important for O-star winds and is suspected to be responsible for fast (~ 0.03 c) outflows in broad absorption-line quasars (BAL QSOs) (Crenshaw, Kraemer, & George 2003). In terms of dynamics, the small opacity to electron scattering (_es = 7 × 10^-25 x cm² per hydrogen atom, with x the ionization fraction) makes this process unimportant relative to radiation pressure acting on dust grains (effective opacity _d ~ 10^-21 cm² per H atom), unless the material under consideration is within the dust sublimation radius, r_subl 1 (L₄₆)^1/2 pc (L₄₆ is the UV/soft X-ray luminosity in units of 10⁴⁶ erg s^-1), and the dust temperature exceeds T_subl 1200 K. Dopita et al. (2002) have shown that dust absorption dominates over photoelectric absorption when U _B / (c _d) ~ 0.01, where _B is the Case B recombination rate to excited states of hydrogen (Osterbrock 1989) and U is the ionization parameter, i.e. the ratio of photon to electron number density. Radiation pressure on dust is therefore probably unimportant in low-luminosity AGN and low-ionization nuclear emission-line regions (LINERs) where U 10^-4 (e.g., Ferland & Netzer 1983; Veilleux & Osterbrock 1987). However, it may dominate the dynamics of narrow emission-line regions (NLRs) in Seyferts and quasars (see Section 5.3) and may be responsible for the similarity of the ionization parameter in these objects (U 0.01; Dopita et al. 2002).

Radiative heating may also be dynamically important in luminous AGN. Krolik, McKee, & Tarter (1981) found that gas at T 10^4.5 K, when exposed to the hard power-law radiation of the AGN, undergoes runaway heating if U 10 - 25. The result is a gas phase at T 10⁶ - 10⁷ K in which Compton cooling balances inverse Compton heating. The sound speed of this gas, c_s = (kT / µm_p)^1/2 300 (T / 10⁷ K)^1/2 km s^-1, exceeds the rotation velocity of typical galaxies. So, gas subject to runaway heating may expel a wind from the host galaxy (Begelman 1985). Given the condition on U, this wind must originate near the nucleus, being fed by gas from the accretion disk itself or nearby (Begelman, McKee, & Shields 1983; Balsara & Krolik 1993 and references therein). For Seyfert galaxies, a substantial wind with T_wind 1 × 10⁶ K and V_wind 200 - 500 km s^-1 is driven off if L / L_Edd 0.08, where L_Edd 3 × 10¹² (M_BH/10⁸ M) L, the Eddington luminosity (e.g., Balsara & Krolik 1993). Unlike starburst-driven winds, Compton-heated AGN winds are directed along the minor axis of the accretion disk and are not necessarily perpendicular to the galactic disk.

Magnetic fields in accretion disks almost certainly play a critical role in powering and collimating AGN winds. Numerical simulations suggest that weakly magnetized accretion disks are subject to magnetorotational instability and inevitably produce magnetically active coronae (e.g., Miller & Stone 2000). The coronae likely generate outflows that are further boosted by centrifugal force (Blandford & Payne 1982; Königl & Kartje 1994). Hydromagnetically boosted outflows may be at the origin of the highly collimated, relativistic jets in powerful radio-loud galaxies (see reviews by Zensus 1997 and Worrall & Birkinshaw 2004). These narrow beams radiate inefficiently (Scheuer 1974), so most of their mechanical energy must heat and agitate the host ISM and the intracluster/intergalactic media (ICM/IGM). The scale over which the mechanical energy of the jets is deposited depends on several factors, including the distribution of ISM near the AGN, the jet power, and how collimated the outflow is at its source. Jets in radio-quiet systems are loosely collimated and barely relativistic (Section 5.2 and Section 5.3).

2.2. Wind-blown bubbles

Depositing mechanical energy by the starburst or the AGN over-pressurizes a cavity of hot gas in the starburst or near the AGN that reaches temperature

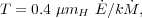(7)

where 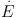is the fraction of the mechanical energy injection rate that is thermalized and is the rate at which the mass is heated. For a starburst, equation (7) can be re-written using equations (1) and (2) and assuming µ = 1.4:

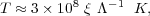(8)

where is the thermalization efficiency of the mechanical energy. The parameter is the mass-loading factor, the ratio of the total mass of heated gas to the mass that is directly ejected by SNe and stellar winds or by the AGN. It accounts for the possibility that some of the ISM is mixed with the stellar or AGN ejecta. Note that this tenuous hot gas will be a poor X-ray (bremsstrahlung) emitter unless / << 1. The central pressure of the cavity is

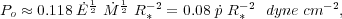(9)

where R_* is the radius of the injection zone (Chevalier & Clegg 1985). R_* is the radius of the star-forming region in the case of a starburst-driven wind. We can rewrite equation (9) using equation (3) in this case:

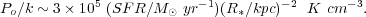(10)

This pressure can significantly exceed the pressure of the undisturbed ISM, hence driving the bubble outflow. The hot cavity then evolves like a stellar wind-blown bubble, whose dynamics were analyzed by several authors (e.g., Castor, McCray, & Weaver 1975; Weaver et al. 1977; Ostriker & McKee 1988; Koo & Mckee 1992a, b). As hot gas expands through the sonic radius, it cools adiabatically (radiative cooling is small in comparison). Beyond the sonic radius, the wind drives a shock into the surrounding ISM and starts to sweep it into a shell of shocked gas. As the bubble boundary expands, the dense shell accumulates ISM and gradually slows the bubble's expansion to much less than the wind velocity. This marks the end of the adiabatic "free expansion" phase, whose duration is set by the mechanical luminosity of the starburst or AGN and the density of the ISM. At high mechanical luminosity (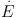 > 10⁴⁶ erg s^-1) and in gas-poor galaxies such as ellipticals (n ~ 0.001 - 0.1 cm^-3), free expansion may continue until the outer shock has traversed much of the host galaxy (e.g., Schiano 1985). In contrast, the free-wind phase in gas-rich starbursts and Seyfert galaxies is too short to observe.

Bubble evolution in gas-rich systems is described by the self-similar Taylor-Sedov solutions to a point-source explosion (blast wave) in a homogeneous medium (Taylor 1950; Sedov 1959). An extension by Schiano (1985) considered a continuous injection of wind energy in the Kompaneets approximation of an exponential atmosphere. After free expansion, the system develops an onion-like structure of five concentric zones; from smallest to largest radii there is (1) the energy injection zone where the mass and energy from the starburst or AGN is injected into the ISM, (2) a free-flowing, supersonic outflow immediately outside the injection zone, (3) a region of hot, shocked wind material, (4) a thin, dense shell of shocked ISM, and (5) undisturbed ISM. Note that the shocked ISM quickly becomes thermally unstable and collapses into a thin shell.

If radiative losses of the overall system are negligible, the expanding bubble is energy-conserving. In that case, the radius and velocity of the expanding shell of shocked ISM are given by (Castor et al. 1975; Weaver et al. 1977)

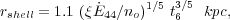(11)

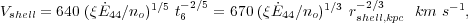(12)

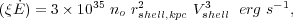(13)

where t₆ is the age of the bubble in Myr, n_o is the ambient density in cm^-3, and 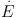₄₄ is the mechanical luminosity of the wind in units of 10⁴⁴ erg s^-1 (see, e.g., Shull & Saken 1995; Oey & Massey 1995; Oey 1996 for more general cases).

Momentum-conserving bubbles - where radiative losses are significant - decelerate faster: r_shell t^1/2; V_shell t^-1/2 r_shell^-1 (e.g., Steigman, Strittmatter, & Williams 1975; Koo & McKee 1992a, 1992b). Their momentum injection rate is

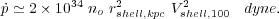(14)

2.3. Galactic winds

Once the shell has formed, if the wind-blown bubble approaches the scale height of the disk H, the shell reaccelerates, begins to fragment through growing Rayleigh-Taylor (RT) instabilities, and finally vents these fragments and the freely flowing and shocked wind into the galaxy halo (e.g., Figure 1). Energy-driven GWs (we discuss momentum-driven winds below) must be sufficiently energetic or long-lived to "breakout". Radiative losses in the wind must be mild enough not to drain too much energy from the wind to stall it; the cooling timescale must exceed the time for the bubble radius (Equation [11]) to reach ~ H. This occurs in the hot GW fluid (MacLow & McCray 1988), unless / << 1 (Equation [8]). The wind will break out if the expansion velocity of the shell (Equation [12]) near H exceeds the effective sound speed of the disk gas. The approximate criterion is

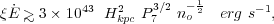(15)

where H_kpc is the disk scale height in kpc and P₇, the ambient pressure P/k in 10⁷ K cm^-3, typical of starbursts (Schiano 1985; MacLow & McCray 1988; Norman & Ikeuchi 1989; MacLow, McCray, & Norman 1989; Koo & McKee 1992a; Strickland et al. 2004b).

Figure 1. An example of a state-of-the-art 3D hydrodynamical simulation of a starburst outflow in an ISM with fractal size distribution at three epochs after the constant energy input wind starts to blow: 1.0 Myr (bottom), 2.5 Myr (middle), and 4.0 Myr (top). Blue is log-density and red is log-temperature (courtesy J. Cooper, G. Bicknell, R. Sutherland).

The steady-flow wind is a strong function of polar angle seen from the starburst: The flow is a free wind up to the critical angle at which its ram pressure becomes comparable to the thermal pressure in the diffuse ISM. At larger angles, a standing bow shock in the galaxy disk decelerates and deflects the wind around undisturbed ISM. The terminal velocity of the wind can be estimated by equating the total energy deposition rate 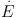to the asymptotic rate of kinetic energy (KE) loss: 1/2 V_∞² 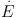. For a starburst-driven wind (eqns. 1 and 2) we obtain

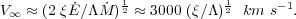(16)

The dependence is easy to understand: cold ISM gas that feels the full brunt of the wind is shock heated and evaporated and eventually mass loads the hot flow, which slows the wind. Equation (16) assumes negligible halo drag.

Because momentum from the starburst or AGN cannot radiate away, a momentum-driven wind may exist even when most of the energy is gone. Then 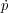= V_∞, where 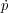is the sum of the radiation and mechanical momentum from the starburst or AGN. Outflow occurs if this exceeds the gravity of the host galaxy (e.g., Murray, Quataert, & Thompson 2005).

2.4. Hydrodynamical Simulations

The main impediment to understanding the dynamical evolution of GWs is that the bulk shocked wind is too hot to be studied by current X-ray observatories. Soft X-ray-emitting gas has been mapped (e.g. Fig. 2 & 3), but is of uncertain origin, seems to fill only a few percent of the volume, and contains at most 10% of the wind mass and energy. Simulations should therefore play a vital role in unraveling the dynamical evolution of this and other gas phases involved in the flow. However, gas at the shock velocities spanned by GWs (~ 20 to 2000 km s^-1; Section 4.4) is unstable both dynamically and thermally: even several percent amplitude, pre-shock density fluctuations (Innes, Giddings, & Falle 1987a, b) are crushed by a 60-fold density increase while cooling to 10⁴ K. Consequently, many computational cells are required to resolve cooling filaments and to track steep gradients. In fact, all but the most recent simulations have had to be two-dimensional, even though such axisymmetry closes "easy" dimensions to entropy flow and thereby forces disorder to emerge in inappropriate ways. Even simulations that adopted axisymmetry could handle only a limited range of gas densities. It was necessary to model separately the collision of the wind with low-density, diffuse ISM, and the collision with higher-density clouds found near the galaxy disk plane.

Axisymmetric simulations have explored a range of disk/halo values (e.g. Tomisaka & Ikeuchi 1988; Tomisaka & Bregman 1993), wind luminosities (e.g. MacLow & Ferrara 1999), mass loadings (Suchkov et al 1996; Hartquist, Dyson, & Williams 1997), metal versus mass-loss rates (especially in dwarf galaxies, e.g. MacLow & Ferrara 1999; D'Ercole & Brighenti 1999), and mass and energy deposition histories in the starburst (e.g. Strickland & Stevens 2000). Denser halos enhance emissivity, and are posited either from a larger dark matter load, or from high-latitude accretion debris that the wind may overrun. A disturbed, rarified, hot atmosphere from previous outbursts has been incorporated into some AGN jet simulations (e.g. Smith et al. 1983), but not yet for starburst winds.

After the wind impacts a dense cloud, (Klein, McKee, & Colella 1994; Silich et al. 1996; Hartquist, Dyson, Williams 1997; Poludnenko, Frank, & Blackman 2002; Williams & Dyson 2002), subsonic flow at the apex becomes transonic around the cloud edges, inducing Kelvin-Helmholtz (KH) instabilities. Clouds therefore soon develop a core/structured halo. Filaments in the halo disappear by photo- or thermal-evaporation before moving far from the core. Schiano, Christiansen, & Knerr (1995, also Vietri, Ferrara, & Miniati 1997) show that the halo penetrates only to the depth of the KH instabilities. The halo ablates from the unscathed core, dumping the entropy induced by the enveloping shocked wind in a series of "shedding events" that "fire polish" the cloud surface to reset the KH clock. By ablating small bumps, the cloud core stabilizes itself against disruptive larger instabilities and can survive to accelerate toward the wind speed.

In more energetic outflows into a denser ISM, mass loading can cause RT instabilities to culminate in repeated, large vortices that crush gas along shocks as the bubble apex shreds. Elsewhere the wind flow can be almost adiabatic, progressing so rapidly that the timescales for recombination, collisional ionization, and excitation exceed greatly the dynamical time (Breitschwerdt & Schmutzler 1999). The gas soon becomes very convoluted, with a fractal size distribution that Sutherland, Bicknell, & Dopita (2003a) show enhances cooling, hence shock prominence, compared to steady-flow models.

Steady winds can develop a "stagnation ring shock" in the disk plane. Tenorio-Tagle & Muñoz-Tuñón (1997, 1998) show how this shock becomes prominent when the ram pressure of even diffuse H I augments the thermal pressure of the enveloping gas. Wind fueling stalls the ring at constant radius, a result consistent with the sparse kinematical data on ring shocks (Section 4.3). Feedback occurs because the base of the wind controls the minimum mass accreted for the starburst to maintain the wind, but computer limitations have thus far prevented coupling of starburst and hydrodynamical codes of useful resolution.

In fact, most winds fail to develop a large-scale, steady flow. The small free-wind zone is then bounded at smallest radius by a few cells of energy injection at the base, and at largest radius by the boundary between dense clouds and their upstream bow shocks that appear as elaborate filamentation at the resolution imposed by the grid. Figures 2 and 3 show that the boundary emits most of the soft X rays. Figure 1 is an example of a recent three-dimensional simulation that, by detailing this region, promises to pin down the elusive X-ray filling factor.