


2.1. Dark Energy or Modified Gravity ?
A cosmological constant is the mathematically simplest, and
perhaps the physically simplest, theoretical explanation for
the accelerating universe. The problem is explaining its unnaturally
small magnitude, as discussed in Sec. 19.4.7 of this Review.
An alternative (which still requires finding a way to make the
cosmological constant zero or at least negligibly small) is that the
accelerating cosmic expansion is driven by a new form of
energy such as a scalar field
[13]
with potential
V( ).
The energy density and pressure of the field
).
The energy density and pressure of the field
 (x)
take the same forms as for inflationary scalar fields, given
in Eq. (19.52) of the Big Bang Cosmology article.
In the limit that
1/2
(x)
take the same forms as for inflationary scalar fields, given
in Eq. (19.52) of the Big Bang Cosmology article.
In the limit that
1/2 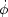 2 ≪
|V(
2 ≪
|V( )|,
the scalar field acts like a cosmological constant, with
p
)|,
the scalar field acts like a cosmological constant, with
p ≈ -
≈ - 
 .
In this scenario, today's cosmic acceleration is closely
akin to the epoch of inflation, but with radically different energy
and timescale.
.
In this scenario, today's cosmic acceleration is closely
akin to the epoch of inflation, but with radically different energy
and timescale.
More generally, the value of w =
p /
/ 
 in scalar
field models evolves with time in a way that depends on
V(
in scalar
field models evolves with time in a way that depends on
V( )
and on the initial conditions
(
)
and on the initial conditions
( i,
i,
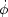 i); some forms of
V(
i); some forms of
V( )
have attractor
solutions in which the late-time behavior is insensitive to initial
values. Many forms of time evolution are possible, including ones
where w is approximately constant and broad classes where w
"freezes" towards or "thaws" away from w = -1, with the transition
occurring when the field comes to dominate the total energy budget.
If
)
have attractor
solutions in which the late-time behavior is insensitive to initial
values. Many forms of time evolution are possible, including ones
where w is approximately constant and broad classes where w
"freezes" towards or "thaws" away from w = -1, with the transition
occurring when the field comes to dominate the total energy budget.
If 
 is even
approximately constant, then it becomes
dynamically insignificant at high redshift, because the matter density
scales as
is even
approximately constant, then it becomes
dynamically insignificant at high redshift, because the matter density
scales as
 m
∝ (1 + z)3. "Early dark energy" models are
ones in which
m
∝ (1 + z)3. "Early dark energy" models are
ones in which 
 is a small but not negligible fraction
(e.g., a few percent) of the total energy throughout the matter and
radiation dominated eras, tracking the dominant component before
itself coming to dominate at low redshift.
is a small but not negligible fraction
(e.g., a few percent) of the total energy throughout the matter and
radiation dominated eras, tracking the dominant component before
itself coming to dominate at low redshift.
Instead of introducing a new energy component, one can attempt to
modify gravity in a way that leads to accelerated expansion
[14].
One option is to replace the
Ricci scalar  with a
function
with a
function  +
f(
+
f( )
in the gravitational action
[15].
Other changes can be more radical, such as introducing extra dimensions
and allowing gravitons to "leak" off the brane that represents
the observable universe (the "DGP" model
[16]).
The DGP example has
inspired a more general class of "galileon" and massive gravity models.
Constructing viable modified gravity models is challenging, in part
because it is easy to introduce theoretical inconsistencies
(such as "ghost" fields with negative kinetic energy)
but above all because GR is a theory with many high-precision empirical
successes on solar system scales
[17].
Modified gravity models typically invoke screening mechanisms
that force model predictions to approach those of GR in regions of
high density or strong gravitational potential.
Screening offers potentially distinctive signatures,
as the strength of gravity (i.e., the effective value of
GN) can vary by order unity in environments with
different gravitational potentials.
)
in the gravitational action
[15].
Other changes can be more radical, such as introducing extra dimensions
and allowing gravitons to "leak" off the brane that represents
the observable universe (the "DGP" model
[16]).
The DGP example has
inspired a more general class of "galileon" and massive gravity models.
Constructing viable modified gravity models is challenging, in part
because it is easy to introduce theoretical inconsistencies
(such as "ghost" fields with negative kinetic energy)
but above all because GR is a theory with many high-precision empirical
successes on solar system scales
[17].
Modified gravity models typically invoke screening mechanisms
that force model predictions to approach those of GR in regions of
high density or strong gravitational potential.
Screening offers potentially distinctive signatures,
as the strength of gravity (i.e., the effective value of
GN) can vary by order unity in environments with
different gravitational potentials.
More generally, one can search for signatures of modified gravity by comparing the history of cosmic structure growth to the history of cosmic expansion. Within GR, these two are linked by a consistency relation, as described below (Equation 2). Modifying gravity can change the predicted rate of structure growth, and it can make the growth rate dependent on scale or environment. In some circumstances, modifying gravity alters the combinations of potentials responsible for gravitational lensing and the dynamics of non-relativistic tracers (such as galaxies or stars) in different ways (see Sec. 19.4.7 in this Review), leading to order unity mismatches between the masses of objects inferred from lensing and those inferred from dynamics in unscreened environments.
At present there are no fully realized and empirically viable modified
gravity theories that explain the observed level of cosmic acceleration.
The constraints on
f( ) models now force
them so close to GR that they cannot produce acceleration without
introducing a separate dark energy component
[18].
The DGP model is empirically ruled out by several tests,
including the expansion history, the integrated Sachs-Wolfe effect,
and redshift-space distortion measurements of the structure growth
rate[19].
The elimination of these models should be considered an important
success of the program to empirically test theories of cosmic acceleration.
However, it is worth recalling that
there was no fully realized gravitational explanation for
the precession of Mercury's orbit prior to the completion of GR in
1915, and the fact that no complete and viable modified gravity
theory exists today does not mean that one will not arise in the future.
In the meantime, we can continue empirical investigations that can
tighten restrictions on such theories
or perhaps point towards the gravitational sector
as the origin of accelerating expansion.
) models now force
them so close to GR that they cannot produce acceleration without
introducing a separate dark energy component
[18].
The DGP model is empirically ruled out by several tests,
including the expansion history, the integrated Sachs-Wolfe effect,
and redshift-space distortion measurements of the structure growth
rate[19].
The elimination of these models should be considered an important
success of the program to empirically test theories of cosmic acceleration.
However, it is worth recalling that
there was no fully realized gravitational explanation for
the precession of Mercury's orbit prior to the completion of GR in
1915, and the fact that no complete and viable modified gravity
theory exists today does not mean that one will not arise in the future.
In the meantime, we can continue empirical investigations that can
tighten restrictions on such theories
or perhaps point towards the gravitational sector
as the origin of accelerating expansion.
2.2. Expansion History and Growth of Structure
The main line of empirical attack on dark energy is to measure the history of cosmic expansion and the history of matter clustering with the greatest achievable precision over a wide range of redshift. Within GR, the expansion rate H(z) is governed by the Friedmann equation (see the articles on Big Bang Cosmology and Cosmological Parameters—Secs. 19 and 21 in this Review). For dark energy with an equation of state w(z), the cosmological constant contribution to the expansion, ΩΛ, is replaced by a redshift-dependent contribution with the evolution of the dark energy density following from Eq. (19.10),
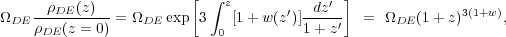 |
(1) |
where the second equality holds for constant w. If Ωm, Ωr, and the present value of Ωtot are known, then measuring H(z) pins down w(z). (Note that ΩDE is the same quantity denoted Ωv in Sec. 19, but we have adopted the DE subscript to avoid implying that dark energy is necessarily a vacuum effect.)
While some observations can probe H(z) directly, others measure the distance-redshift relation. The basic relations between angular diameter distance or luminosity distance and H(z) are given in Ch. 19 —and these are generally unaltered in time-dependent dark energy or modified gravity models. For convenience, in later sections, we will sometimes refer to the comoving angular distance, DA,c(z) = (1 + z) DA(z).
In GR-based linear perturbation theory, the density contrast
δ(x, t) ≡
 (x,
t)
/
(x,
t)
/  (t)
- 1 of pressureless matter grows in proportion to the linear growth
function G(t) (not to be confused with the gravitational
constant GN), which follows the differential equation
(t)
- 1 of pressureless matter grows in proportion to the linear growth
function G(t) (not to be confused with the gravitational
constant GN), which follows the differential equation
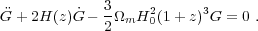 |
(2) |
To a good approximation, the logarithmic derivative of G(z) is
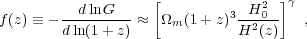 |
(3) |
where γ ≈ 0.55 for relevant values of cosmological parameters [20]. In an Ωm = 1 universe, G(z) ∝ (1 + z)-1, but growth slows when Ωm drops significantly below unity. One can integrate Equation 3 to get an approximate integral relation between G(z) and H(z), but the full (numerical) solution to Equation 2 should be used for precision calculations. Even in the non-linear regime, the amplitude of clustering is determined mainly by G(z), so observations of non-linear structure can be used to infer the linear G(z), provided one has good theoretical modeling to relate the two.
In modified gravity models the growth rate of gravitational clustering may differ from the GR prediction. A general strategy to test modified gravity, therefore, is to measure both the expansion history and the growth history to see whether they yield consistent results for H(z) or w(z).
Constraining a general history of w(z) is nearly impossible, because the dark energy density, which affects H(z), is given by an integral over w(z), and distances and the growth factor involve a further integration over functions of H(z). Oscillations in w(z) over a range Δz / (1 + z) ≪ 1 are therefore extremely difficult to constrain. It has become conventional to phrase constraints or projected constraints on w(z) in terms of a linear evolution model,
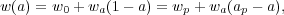 |
(4) |
where a ≡ (1 + z)-1, w0 is the value of w at z = 0, and wp is the value of w at a "pivot" redshift zp ≡ ap-1 - 1, where it is best constrained by a given set of experiments. For typical data combinations, zp ≈ 0.5. This simple parameterization can provide a good approximation to the predictions of many physically motivated models for observables measured with percent-level precision. A widely used "Figure of Merit" (FoM) for dark energy experiments [21] is the projected combination of errors [σ(wp)σ(wa)]-1. Ambitious future experiments with 0.1-0.3% precision on observables can constrain richer descriptions of w(z), which can be characterized by principal components.
There has been less convergence on a standard parameterization for describing modified gravity theories. Deviations from the GR-predicted growth rate can be described by a deviation Δγ in the index of Equation 3, together with an overall multiplicative offset relative to the G(z) expected from extrapolating the CMB-measured fluctuation amplitude to low redshift. However, these two parameters may not accurately capture the growth predictions of all physically interesting models. Another important parameter to constrain is the ratio of the gravitational potentials governing space curvature and the acceleration of non-relativistic test particles. The possible phenomenology of modified gravity models is rich, which enables many consistency tests but complicates the task of constructing parameterized descriptions.
The more general set of cosmological parameters is discussed elsewhere in this Review (Sec. 21), but here we highlight a few that are particularly important to the dark energy discussion:
The dimensionless Hubble parameter h ≡ H0 / 100 km s-1 Mpc-1 determines the present day value of the critical density and the overall scaling of distances inferred from redshifts.
Ωm and Ωtot affect the expansion history and the distance-redshift relation.
The sound horizon rs = ∫0trec cs(t) dt / a(t), the comoving distance that pressure waves can propagate between t=0 and recombination, determines the physical scale of the acoustic peaks in the CMB and the baryon acoustic oscillation (BAO) feature in low redshift matter clustering [22].
The amplitude of matter fluctuations, conventionally represented by the quantity σ8(z), scales the overall amplitude of growth measures such as weak lensing or redshift-space distortions (discussed in the next section).
Specifically, σ8(z) refers to the rms
fluctuation of the matter overdensity
 /
/
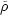 in
spheres of radius 8 h-1 Mpc, computed from the linear
theory matter power spectrum
at redshift z, and σ8 on its own refers to the value
at z = 0 (just like our convention for Ωm).
in
spheres of radius 8 h-1 Mpc, computed from the linear
theory matter power spectrum
at redshift z, and σ8 on its own refers to the value
at z = 0 (just like our convention for Ωm).
While discussions of dark energy are frequently phrased in terms of values and errors on quantities like wp, wa, Δγ, and Ωtot, parameter precision is the means to an end, not an end in itself. The underlying goal of empirical studies of cosmic acceleration is to address two physically profound questions:
Does acceleration arise from a breakdown of GR on cosmological scales or from a new energy component that exerts repulsive gravity within GR?
If acceleration is caused by a new energy component, is its energy density constant in space and time, as expected for a fundamental vacuum energy, or does it show variations that indicate a dynamical field?
Substantial progress towards answering these questions, in particular any definitive rejection of the cosmological constant "null hypothesis," would be a major breakthrough in cosmology and fundamental physics.