


In the standard hierarchical scenario, galaxy mergers play a large role in mass assembly, and one of the results of the repeated coalescence of galaxies is to randomly average out the angular momentum of the system, and to form spheroids (e.g. Toomre 1977, Barnes & Hernquist 1991, Naab & Burkert 2003, Bournaud et al. 2005, 2007a). In these last works, it was shown how repeated minor mergers progressively accumulate stars in a central spheroid and grow the bulge, to transform the galaxy in a more early-type spiral. Eventually, N minor mergers of mass ratio N:1 result in an elliptical remnant quite similar to those formed in a 1:1 merger. As shown by Barnes (1988), mergers are very efficient in forming long tidal tails while the main baryonic components merge quickly, because of the existence of extended and massive dark halos, which take the orbital angular momentum away. It can then be expected that the frequency of mergers will depend crucially on the model assumed for the missing mass.
One of the main questions is to know whether the MOND dynamics is able to produce long tails in major mergers of galaxies, like in the prototypical Antennae system (Figure 2). These tails have also helped to constrain the dark matter halos potential (Dubinski et al. 1996). With MOND, the result is not easy to predict, and numerical simulations are necessary, since the External Field Effect (EFE) perturbs the MONDian dynamics in the outer parts of galaxies. This new effect particular to MOND comes from the fact that it violates the Strong Equivalence Principle of General Relativity. In the Newtonian frame, the internal gravitational forces of a system are independent of their external environment: if the object is embedded in a large system, exerting a force which can be considered constant all over the object, then the internal dynamics is unchanged. Of course, if the force is varying across the object, its differential gives rise to tidal forces, which impact the object. But in the MOND dynamics, even a constant force may create an acceleration above the critical one a0, and get the object out of the MOND regime (Milgrom 1983, 1998).
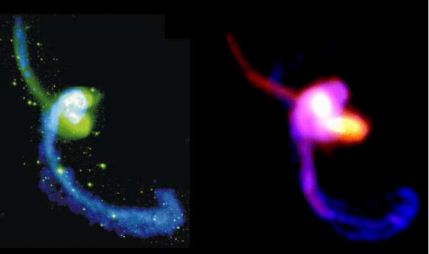 |
Figure 2. Simulation of tidal interactions in a major merger in MOND (right, with gas in blue and stars in red) compared to the Antennae galaxies (Hibbard et al. 2001, HI gas in blue, and stars in green). The two long tidal tails are reproduced (Tiret & Combes 2008b). |
Several cases can be distinguished to model the EFE, according to the respective values of the external acceleration ae with respect to the internal acceleration a of the object under consideration, and the critical acceleration a0. If ae < a < a0, then the standard MOND effects are retrieved, and if a < a0 < ae, then the EFE is strong enough to make the system purely Newtonian. But in the intermediate regime, where a < ae < a0 then the system is Newtonian with a renormalised gravitational constant G. It can be estimated for instance in a one-dimensional system, that the effective gravitational constant is then Geff = G [µe(1 + Le)]−1 where µe = µ(ae / a0) and Le is the logarithmic gradient of µ (Famaey & McGaugh 2012). In the outer parts of a given system, the internal acceleration is always vanishing, and there will always be a small ae < a0, therefore this represents the general case: the gravitational force falls again as 1/r2, and the potential as 1/r and not logarithmically, as could be extrapolated. This allows to define the escape velocity of the system, as in the Newtonian case. Computations of the EFE in the Milky Way, due to the nearby Andromeda galaxy, have given results compatible with the observations (Wu et al. 2007).
Simulations with a 3D adaptive-mesh code able to solve the MOND equations, and including gas and stars, have shown that two long tidal tails can develop in a major merger similar to the Antennae (cf Figure 2). In absence of dark matter particles as receivers of the orbital angular momentum of the two galaxies, baryons are playing this role, and tidal tails can be very long. In addition, tidal dwarf galaxies can be naturally formed at the tip of the tidal tails in MOND, while it requires radially extended dark matter halos in the standard model (Bournaud et al. 2003). The big difference between the two models is the efficiency of the dynamical friction. While mergers can take only one orbit, or less than one Gyr in the standard model, it will take several Gyrs with MOND, and mergers will occur only with selected impact parameters, and initial relative angular momenta. At a distance of ∼ 100 kpc, two galaxies in circular orbits will not merge in a Hubble time with MOND (Figure 3). On the contrary, in the standard model, galaxies have already plunged well inside their dark matter halos, of radius ∼ 200 kpc. Then local dynamical friction is already effective, while in the MOND case, the relative decay relies only on the friction at distance, which is much weaker.
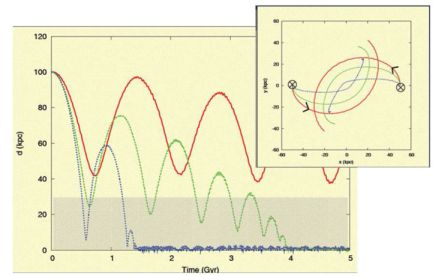 |
Figure 3. Radial decay during the tidal interactions between two equal-mass spiral galaxies, in the MOND model (Tiret & Combes 2008b). At left is shown the relative distance in kpc versus time in Gyr, while the insert at right shows the corresponding trajectories. (image by O. Tiret). |
As described above, the gravitational forces between galaxies at large distance are likely to vary as 1/r2 as in the Newtonian regime, but with a boosted constant, so the long-distance approach of galaxies could be thought similar. However the phenomena associated to dynamical friction are completely different. Answers to this problem have been controversial at the start, since Ciotti & Binney (2004) computed the relaxation time in the MOND regime with strong approximations: very small fluctuations, impulse approximation for deflection or orbits, linear summation of effects, etc. and they compare this two body relaxation time with that in the Newtonian regime, considering the dark matter halo as a rigid background, not participating in the fluctuations. Then they extrapolate their finding of a shorter relaxation time in MOND to the dynamical friction time, obtained for test particles for the local formula of Chandrasekhar (1943), and conclude that globular clusters should spiral inwards to the center in dwarf galaxies in a few dynamical time-scales, as well as galaxies in groups and in clusters. Nipoti et al. (2008) tried to confirm these findings in simulations, by applying the same hypotheses of a tiny perturbation: the massive bodies subject to the friction, either globular clusters or a rigid bar, have to contain less than 5% of the baryonic mass, so that particles absorbing the energy and angular momentum are not globally perturbed. In realistic systems though, Nipoti et al. (2007) found that the merging timescales for spherical systems are significantly longer in MOND than in Newtonian gravity with dark matter, and Tiret & Combes (2007) found that bars keep their pattern speed constant in MOND, while they are strongly slowed down in the Newtonian equivalent system with a dark matter halo. In summary, dynamical friction is very slow in MOND, since galaxies are not embedded in extended and massive spheroids of dark matter particles, able to accept the orbital angular momentum. A short merging time-scale for equal-mass interacting galaxies, as short as the CDM, is possible only for nearly radial orbits. Although the impact of very small fluctuations could be larger in MOND than in Newtonian dynamics, the effect saturates quickly when the perturbation is no longer infinitesimal, and on the contrary the equivalent Newtonian system with dark matter has shorter response time-scales, and a massive body (either a companion, or a galactic bar) is slowed down very efficiently. The case of bars, their pattern speeds, and their impact on bulge formation will be detailed in the next Section 3.
Could the smaller merger frequency predicted by MOND be tested in observations? Unfortunately, the actual merger frequency is not directly accessible. Observers tend to quote galaxy pair frequency, or starbursts due to mergers (e.g. Bell et al. 2006, Lopez-Sanjuan et al. 2013, Stott et al. 2013). However, there is a degeneracy here, since galaxy can appear in pairs during either a short or long time-scale, and starbursts can occur at each closer passage. In the standard DM models, an assumption is done on the duration of galaxy interactions, and the number of starbursts: according to the initial relative velocity and the geometry of the encounter, the merger is expected to occur in one or two passages. An intense starburst is associated to the final phase, and the number of starbursts is thought to count the number of mergers (e.g. Di Matteo et al 2007). In the MOND model, many passages in binary galaxies will be required before the final merging, and a starburst may be triggered at each pericenter. The number of starbursts as a function of redshift could then be similar, and cannot discriminate the two models. The degeneracy cannot be raised between a limited number of long-lived mergers, or a high frequency of short-lived mergers.