


Brooks & Christensen (2015) is perhaps the most important chapter in this book. The mainstream of theoretical work on galaxy formation has come to be the simulation in a cosmological context first of purely collisionless CDM but now with gloriously messy baryonic physics included. Progress is impressively rapid, but we are far from finished. This subject is well reviewed from the perspective of its practitioners by Brooks and Christensen. This includes a discussion of uncertainties and shortcomings in the models, again as seen by theorists. As an observer, I have a complementary perspective on which measurements of galaxies provide the most useful constraints on and “targets” for formation models. It gives me the feeling that modelers are at least partly “barking up the wrong tree.” This section complements Brooks and Christensen (2015) by reviewing these observations.
Pseudobulge formation was covered in Section 2. Here, I focus on the formation of classical bulges and ellipticals. My discussion uses the observations that classical bulges are essentially indistinguishable from coreless-disky-rotating ellipticals (see, e.g., Figure 4). The inference is that they formed in closely related ways.
4.1. Observer's Perspective on Bulge Formation Via Major Mergers
I begin with giant ellipticals and classical bulges: their structure and formation are understood in the most detail. Classical bulges are identified by the criteria listed in Kormendy & Kennicutt (2004), Kormendy (2012), KH13, Fisher & Drory (2015), and Section 2 here. I know no observational reason to seriously doubt our understanding of bulges with B / T ≳ 0.8. Then, as B / T drops to ≲ 1/2, the situation gets less clear. Our formation picture may still essentially be correct, but it gets less directly based on observations as B / T or bulge luminosity decreases. Meanwhile, the theoretical problem is that simulations make too many bulges, especially big ones. In this section, I review things that we know and outline things that we do not know. It is critically important to start with a discussion of ellipticals, because our understanding of classical bulges must be within this context.
4.1.1. Observed Properties of Ellipticals: Clues to Their Formation
The observed properties of elliptical galaxies are reproduced by simulations of wet and dry mergers in remarkable detail. These are not embedded in large-scale cosmological simulations, but this is not a fundamental fault if the initial conditions are realistic – galaxies with typical z ∼ 0 gas fractions and encounter velocities that are roughly parabolic. Kormendy et al. (2009, hereafter KFCB) provide an ARA&A-style review and develop some of the evidence. Hopkins et al. (2009a and 2009b) provide the most detailed models for wet and dry mergers, respectively. These papers are comprehensive; a concise summary of the “E – E dichotomy” in Kormendy (2009) is updated below. The critical observation is that ellipticals come in two varieties and that bulges are similar to one (but not both) of these varieties.
The E – E dichotomy of ellipticals into two kinds is based on these observations:
Giant ellipticals (MV ≲ −21.5
± 1 for H0 = 70 km s−1
Mpc−1) generally
(1) have Sérsic function outer profiles with n > 4;
(2) have cores; i.e., central missing light with respect to the outer
Sérsic profile;
(3) rotate slowly, so rotation is of little importance dynamically;
hence
(4) are anisotropic and modestly triaxial;
(5) are less flattened (ellipticity є ∼ 0.2) than smaller
ellipticals;
(6) have boxy-distorted isophotes;
(7) mostly are made of very old stars that are enhanced in α
elements (Figure 2);
(8) often contain strong radio sources (Figure 3), and
(9) contain X-ray-emitting gas, more of it in more luminous galaxies
(Figure 3).
Normal ellipticals and dwarf ellipticals like M32
(MV ≳−21.5) generally
(1) have Sérsic function outer profiles with n ≃ 2 to
3;
(2) are coreless – have central extra light with respect to the
outer Sérsic profile;
(3) rotate rapidly, so rotation is dynamically important to their
structure;
(4) are nearly isotropic and oblate spheroidal, albeit with small axial
dispersions;
(5) are flatter than giant ellipticals (ellipticity є ∼
0.35);
(6) have disky-distorted isophotes;
(7) are made of younger stars with little α-element enhancement
(Figure 2);
(8) rarely contain strong radio sources (Figure 3),
and
(9) generally do not contain X-ray-emitting gas
(Figure 3).
These results are etablished in many papers (e. g., Davies et al. 1983; Bender 1988; Bender et al. 1989; Nieto et al. 1991; Kormendy et al. 1994; Lauer et al. 1995, 2005, 2007a, b; Kormendy & Bender 1996; Tremblay & Merritt 1996; Gebhardt et al. 1996; Faber et al. 1997; Rest et al. 2001; Ravindranath et al. 2001; Thomas et al. 2002a, b, 2005; Emsellem et al. 2007, 2011; Cappellari et al. 2007, 2011, 2013b; KFCB; Kuntschner et al. 2010). A few ellipticals are exceptions to one or more of (1) – (9). The above summary is quoted from Kormendy (2009).
Why is this relevant here? The answer is that classical bulges are closely similar to coreless-disky-rotating ellipticals. No bulge is similar to a core-boxy-nonrotating elliptical as far as I know. This is a clue to formation processes. First, though, we need to understand the difference between the two kinds of ellipticals:
How did the E – E dichotomy arise? The “smoking gun” for an explanation is a new aspect of the dichotomy originally found in Kormendy (1999) and observed in all low-luminosity ellipticals in the Virgo cluster by KFCB. Coreless galaxies do not have featureless power-law profiles. Rather, all coreless galaxies in the KFCB sample show a new structural component, i. e., central extra light above the inward extrapolation of the outer Sérsic profile. Kormendy (1999) suggested that the extra light is produced by starbursts fed by gas dumped inward during dissipative mergers. Starbursts were predicted by merger simulations as soon as these included gas, dissipational gas inflow, and star formation (Mihos & Hernquist 1994). Mihos and Hernquist were concerned that extra components had not been observed. The reason turns out to be that we had not measured ellipticals with enough surface brightness range and spatial resolution. Like Faber et al. (1997, 2007), KFCB suggest that the origin of the E – E dichotomy is that core ellipticals formed in dry mergers whereas coreless ellipticals formed in wet mergers. Simulations of dry and wet mergers reproduce the structural properties of core and extra light ellipticals in beautiful detail (Hopkins et al. 2009a, b). And, although the formations scenarios differ, Khochfar et al. (2011) similarly conclude that the difference between fast and slow rotators is related to cold gas dissipation and star-formations shutdown, respectively.
Cores are thought to be scoured by supermassive black hole binaries that were formed in major mergers. The orbit shrinks as the binary flings stars away. This decreases the surface brightness and excavates a core (Begelman et al. 1980; Ebisuzaki et al. 1991; Makino & Ebisuzaki 1996; Quinlan & Hernquist 1997; Faber et al. 1997; Milosavljević & Merritt 2001; Milosavljević et al. 2002; Merritt 2006). The same process should happen during wet mergers; in fact, gas accelerates the orbital decay (Ivanov, Papaloizou, & Polnarev 1999; Gould & Rix 2000; Armitage & Natarajan 2002, 2005; Escala et al. 2004, 2005; Dotti et al. 2007; Hayasaki 2009; Cuadra et al. 2009; Escala & Del Valle 2011; see Mayer 2013 for a recent review). However, we observe that the fraction of the luminosity that is in extra light in low-luminosity ellipticals is larger than the fraction of the light that is “missing” in the cores of high-luminosity ellipticals. KFCB suggest that core scouring is swamped by the starburst that makes the extra light in coreless-disky-rotating ellipticals.
When did the E – E dichotomy arise? Figure 2 shows observation (7) that core ellipticals mostly are made of old stars that are enhanced in α elements. In contrast, coreless ellipticals are made of younger stars with more nearly solar compositions. This means (Thomas et al. 2002a, b, 2005) that the stars in core Es formed in the first few billion years of the universe and over a period of ≲ 1 Gyr, so quickly that Type I supernovae did not have time to dilute with Fe the α-enriched gas recycled by Type II supernovae. This does not mean that core ellipticals were made at the same time as their stars. Mass assembly via dry mergers as required to explain their structure could have happened at any time after star formation stopped. Our problem is to explain how star formation was quenched so quickly and not allowed to recur. In contrast, coreless ellipticals have younger, less-α-enhanced stellar populations. They are consistent with a simple picture in which a series of wet mergers with accompanying starbursts formed their stellar populations and assembled the galaxies more-or-less simultaneously over the past 9 billion years. Faber et al. (2007) discuss these issues in detail. A big problem with the present state of the art is that we know so little about mergers and merger progenitors at high z.
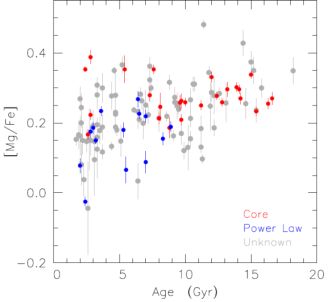 |
Figure 2. Alpha element overabundance (log solar units) versus relative age of the stellar population. Red and blue points denote core and “power law” (i.e., coreless) ellipticals. The [Mg/Fe] and age data are from Thomas et al. (2005); this figure is from KFCB. |
Why did the E – E dichotomy arise? The key observations are: (8) core-boxy ellipticals often are radio-loud whereas coreless-disky ellipticals are not, and (9) core-boxy ellipticals contain X-ray gas whereas coreless-disky ellipticals do not (Bender et al. 1989). Figure 3 (from KH13) illustrates these results. KFCB suggest that the hot gas keeps dry mergers dry and protects giant ellipticals from late star formation. This is the operational solution to the above “maintenance problem”. I return to the problem of star-formation quenching in Section 7.
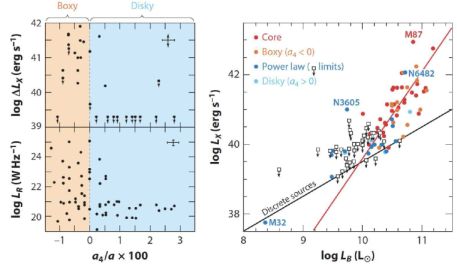 |
Figure 3. (Left) Correlation with isophote shape parameter a4 of (top) X-ray emission from hot gas and (bottom) radio emission (from Bender et al. 1989). Boxy ellipticals (a4 < 0) contain hot gas and strong radio sources; disky ellipticals (a4 > 0) generally do not. (Right) KFCB update of the X-ray correlation. Detections are color-coded according to the E – E dichotomy. The emission from X-ray binary stars is estimated by the black line (O'Sullivan, Forbes, & Ponman 2001); this was subtracted from the total emission in constructing the left panels. The red line is a bisector fit to the core-boxy-nonrotating ellipticals. They statistically reach LX = 0 from hot gas at logLB ≃ 9.4. This corresponds to MV ≃ −20.4, a factor of 2 fainter than the luminosity that divides the two kinds of ellipticals. Thus, if a typical core E was made in a merger of two equal-mass galaxies, then both were marginally big enough to contain X-ray gas and the remnant immediately was massive enough so that hot gas could quench star formation. KFCB suggest that this is why these mergers were dry. For similar results, see Pellegrini (1999, 2005) and Ellis & O'Sullivan (2006). |
In the above story, the challenge is to keep the hot gas hot, given that X-ray gas cooling times are short (Fabian 1994). KFCB review evidence that the main heating mechanism may be energy feedback from accreting BHs (the active galactic nuclei [AGNs] of observation 8); these may also have helped to quench star formation. Many details of this picture require work (Cattaneo et al. 2009). Cosmological gas infall is an additional heating mechanism (Dekel & Birnboim 2006). Still, Figure 3 is a crucial connection between X-ray gas, AGN physics, and the E – E dichotomy.
“Bottom line:” In essence, only giant, core ellipticals and their progenitors are massive enough to contain hot gas that helps to engineer the E – E dichotomy.
4.1.2. Classical Bulges Resemble Coreless-Disky-Rotating Ellipticals
Are both kinds of ellipticals also found as bulges? So far, observations indicate that the answer is “no”. Classical bulges closely resemble only the coreless-disky-rotating ellipticals. There are apparent exceptions in the literature, but all the exceptions that I know about are classification errors brought about (e.g.) by the very large Sérsic indices of some core galaxies (see KFCB Table 1 for examples and KFCB Section 5.2 for discussion). This comment also does not include ellipticals with nuclear disks. All signs are that these involve different physics, so these really are ellipticals, not S0 bulges.
There is physics in this conclusion. The X-ray gas prevents cooling and dissipation during any subsequent mergers or any z ≲ 1 cold accretion. Plausibly, it should also prevent there from being any cold gas left over to make a new disk after a merger is complete. Further checks, both of the observational conclusion and of the theoretical inference, should be made.
4.1.3. The Critically Important Target for Galaxy Formation
The most fundamental distinction between galaxy types is the one between bulges + ellipticals and disks. Bulges and disks overlap over a factor of about ∼1500 in luminosity and mass (Figure 4), but over that entire overlap range, they are dramatically different from each other. This includes differences in specific angular momentum (Romanowsky & Fall 2012; Fall & Romanowsky 2013), in orbit structure, in flattening, and in radial density profiles (disks are roughly exponential; coreless-disky-rotating ellipticals have n ≳ 2). At absolute magnitude MV ≃ −16.7 and outer circular-orbit rotation velocity Vcirc ∼ 85 km s−1, MM32 is a normal small elliptical galaxy (KFCB). At MV ≃ −21.6 and Vcirc = 210 ± 15 km s−1, M101 is almost 100 times more luminous but is thoroughly different from MM32 (Kormendy et al. 2010).
I believe that the goal of galaxy formation modeling should be to produce realistic disks and realistic ellipticals that overlap over the observed factor of ∼ 1500 in luminosity but that differ as we observe them to differ over the whole of that range. And over the whole of that range, disks and bulges can be combined with B / T and D / T ≃ 1 − B / T ratios that have the observed distribution (i.e., B / T ∼ 1 near the upper end of the range, but it can be ≪ 1 at the bottom of the range). The properties of individual disks and bulges are essentially independent of B / T with structural parameters shown in Figure 4.
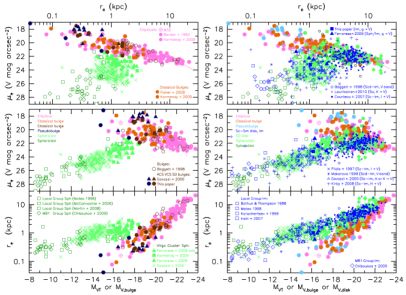 |
Figure 4. Correlations between effective radius re, effective brightness µV, and absolute magnitude MV for classical bulges and ellipticals (brown and pink points), for spheroidal (Sph) galaxies and S0 disks (green points), and for spiral galaxy disks (blue points). When bulge-disk decomposition is necessary, the two components are plotted separately. Bulges and disks overlap from MV ≃ −15 to MV ≃ −23, i.e., over a factor of about 1500. The left panel shows (1) that Sph galaxies are distinct from bulges + ellipticals and (2) that classical bulges and ellipticals satisfy the same structural parameter correlations. The right panel adds S0 and S galaxy disks. It shows that all disks satisfy the same structural parameter correlations over the whole range of luminosities. Note that disks and ellipticals have similar re and µe at the highest luminosities, but they have very different Sérsic indices (∼ 1 and 2 to > 10, respectively). As a result, the central surface brightnesses in bulges and ellipticals are more than an order of magnitude higher than the central surface brightnesses of disks (Kormendy 1985, 1987). Bulges + ellipticals and disks also have non-overlapping distributions of intrinsic flattening (e.g., Sandage, Freeman, & Stokes 1970). From Kormendy & Bender (2012). |
Of course, bulges and disks are not different in every parameter; e.g., the re – µe correlations overlap at high luminosities (Figure 4). This makes sense: At the highest masses, it does not require much dissipation to turn a disk into an elliptical, at least in terms of virial parameters. All that is required is to scramble disk orbits into an ellipsoidal remnant. A larger amount of dissipation is required to make the high-density centers, and in central parameters and parameter correlations, disks and bulges + ellipticals are very different (Kormendy 1985, 1987).
The most difficult challenge in our picture of galaxy formation – I suggest – is to understand how hierarchical clustering produces so many giant, pure-disk galaxies that have no sign of a classical bulge. CDM halos grow by merging; fragments arrive from all directions, and not all fragments are small. There are two parts to this problem: (1) It is difficult to understand how cold, flat disks survive the violence inherent in the mergers that grow DM halos. And (2) it is difficult to prevent the stars that arrive with the latest accretion victim from adding to a classical bulge that formed in (1) from the scrambled-up disk.
Brooks & Christensen (2015) review how the modeling community tries to solve this problem. In spite of several decades of evidence that mergers make bulges, they do not use mergers to turn disks into bulges. Instead, they use feedback from young stars and active galactic nuclei to “whittle away” the low-angular-momentum part of the distribution of gas angular momenta and argue that this prevents bulge formation. And they use feedback to delay disk formation until the halo is assembled. Feedback is likely to be important in the formation of dwarf galaxies (Governato et al. 2010), and indeed, they essentially never have bulges (e.g., Kormendy & Freeman 2015, Figure 10).
However, it is difficult for me to believe that feedback, either from star formation or from AGNs, is responsible for the difference between bulges and disks. Feedback is fundamentally an internal process that is controlled by the galaxy's potential well depth. It is not clear how only tweaking the feedback can make a small elliptical like MM32 (different from small disks) and a giant disk like M101 (different from similarly giant ellipticals) with no intermediate cases. Bulge-to-total ratios vary widely, but classical bulges are always like ellipticals no matter what the B/T ratio, and disks are always different from ellipticals no matter what the D/T ratio. Observations do not suggest that it is primarily feedback that results in this difference. Rather:
There is a fundamental observational clue that modelers are not using:
Whether evolution makes disks or whether it makes bulges does not depend mainly on galaxy mass. Rather, it is a strong function of environment. Kormendy et al. (2010) show that, in the extreme field (i.e., in environments like the Local Group), most giant galaxies (Vcirc ≥ 150 km s−1) are pure disks. Only 2 of 19 giant galaxies closer to us than 8 Mpc have B / T as big as 1/3. Only 2 more are ellipticals. A few have smaller classical bulges, but 11 of the 19 galaxies have essentially no classical bulge. In contrast, > 2/3 of all stars in the Virgo cluster live in bulges or elliptical galaxies. There is no problem of understanding giant pure-disk galaxies in the Virgo cluster. It is a mature, dense environment that contains large amounts of X-ray-emitting, hot gas. Rich clusters are places where most of the baryons live suspended in hot gas (e.g., Kravtsov & Borgani 2012). I argue in Section 4.1.1 that various heating processes maintain this situation for very long times. In contrast, poor groups are environments in which accretion of cold gas from the cosmic web can dominate, as long as the galaxies involved – i.e., the aforementioned pure disks – are low enough in mass so that they cannot hold onto X-ray gas.
As long as this environmental dependence is not a primary, essential part of the explanation, I believe that attempts to solve the problem of overproduction of bulges in ΛCDM cosmology are “barking up the wrong tree”.
Why can'st we use feedback to delay star formation until the halo is assembled? As reviewed by Brooks & Christensen (2015), this is commonly suggested. The counterexample is our Galaxy: The oldest stars in the thin disk are ∼ 1010 yr old, so much of the growth of our Galaxy happened when the thin disk was already in place (Kormendy et al. 2010, p. 73).
4.1.5. It is not a problem that major mergers are rare
The prevailing theoretical paradigm is more and more converging on the view that major mergers are rare – are, in fact, almost irrelevant – and that, instead, minor mergers make both bulges and ellipticals (see Naab 2013 for a review), even some core-boxy-nonrotating ellipticals (Naab et al. 2014). It will be clear from this writeup that, based on observational evidence, I agree that major mergers are rare. But I disagree that they are unimportant in the formation of bulges and ellipticals.
The above papers make important points that are robust. They argue convincingly that major mergers are rare – that only a small fraction of galaxies undergo several of them in their recent history (say, since z ∼ 2). And many authors argue that most star formation does not occur during mergers; rather, it occurs in a “main sequence” of disks of various masses, with higher star formation rates at higher masses (e.g., Schiminovich et al. 2007; Noeske et al. 2007; Elbaz et al. 2007; Daddi et al. 2007; Finlator & Davé 2008; Karim et al. 2011; Peng et al. 2010; Rodighiero et al. 2011; Wuyts et al. 2011; Salmi et al. 2012; Whitaker et al. 2012; Tacconi et al. 2013; Speagle et al. 2014). These authors conclude that the duty cycle of star formation is large. Therefore most star formation does not occur in rare events. I made the same argument in Section 2: If almost all galaxies of a particular type are energetically forming stars, then star formation must be secular; it cannot be episodic with short duty cycles. Caveat: the star formation that is associated with mergers is not instantaneous. Puech et al. (2014) argue that merger-induced star formation is significant. Are these results consistent with a picture in which essentially all formation of classical bulges and ellipticals happens via major mergers?
I believe that the answer is yes, although the details need further work. Elliptical galaxies are observed to be rare; the morphology-density relation (Dressler 1980; Cappellari et al. 2011) shows that they are a small fraction of all galaxies except in rich clusters. Classical bulges are rarer than we thought, too; this is a clear conclusion of the work on disk secular evolution. Therefore the events that make bulges must be rare. It is also not a problem if most star formation happens in disks. For example, only a small fraction of the galaxy mass is contained in the extra light components that are identified by KFCB and by Hopkins (2009a) as the parts of coreless/disky/rotating ellipticals that formed in the most recent ULIRG-like starburst (e.g., Genzel et al. 2001). Most of the mass was already in stars before these late, wet mergers. And in dry mergers, essentially all the mass was already in stars (or in X-ray gas that stays X-ray gas) and essentially no new stars are formed.
How many mergers do we need to explain elliptical galaxies? Toomre (1977) already pointed out that a reasonable increase in merger rate with increasing z would suffice. He based this on ten mergers-in-progress that he discussed in his paper. He assumed that such objects are identifiable for ∼ half a billion years. Then, if the number of mergers in progress increased as (lookback time)5/3 consistent with a flat distribution of binding energies for galaxy pairs, the result is that the number of remnants is consistent with the number of elliptical and early-type disk galaxies. This estimate was made for the level of completeness of the Second Reference Catalogue of Bright Galaxies (de Vaucouleurs, de Vaucouleurs, & Corwin 1976).
Conselice (2014) reviews observational estimates of how merger rates depend on z. As Toomre predicted, the major merger rate is inferred – e.g., from counting close pairs of galaxies – to increase rapidly with z. Observations of high-z galaxies show that close binary fractions increase roughly as (1 + z)m with m ∼ 2 to 3 (e.g., Bluck et al. 2009, 2012; Conselice et al. 2009; López-Sanjuan et al. 2013; Tasca et al. 2014). ULIRGs increase in comoving energy density even faster toward higher redshift, at least out to z = 1 (Le Floc'sh et al. 2005). The necessary connections between these results to establish or disprove whether bulges + ellipticals are made via major mergers have not been established. Important uncertainties include (1) the low-mass end of the mass functions for ellipticals and especially for classical bulges, and (2) the degree to which mass-clump sinking in disks contributes. However, the above results on merger frequencies appear at least qualitatively consistent with the conclusion that bulges and ellipticals are made in major mergers, as the pre-2000 history of observational work established (see Schweizer 1998 for a review).
A shortcoming of many current investigations is that they concentrate on a few parameter distributions for large galaxy samples and not specifically on the histories of bulges and disks. E.g., they look at the statistics of what fraction of galaxies experience mergers. Outcomes are difficult to estimate, because with samples of 104 to 105 z ∼ 0 galaxies or 102 high-z galaxies, the typical galaxy is only a few pixels in radius. Then it is difficult to identify and classify galaxy components.
4.1.6. Uncertainties With Our Picture of Bulge Formation in Major Mergers
Two major uncertainites are a concern (see also Brooks & Christensen 2015). Virtually all observational evidence on mergers-in-progress (e.g., Toomre 1977; Joseph & Wright 1985; Sanders et al. 1988a, b; Hibbard et al. 1994, 1995, 1996, 2001a, b; see Schweizer 1987, 1990, 1998 for reviews) involves giant galaxies. And the detailed evidence is for z ∼ 0 galaxies with gas fractions of a few to ∼ 10%. (1) We do not have comparable evidence for dwarfs. That is, we have not studied a sample of dwarfs that fill out a merger sequence from close pairs to mergers engaged in violent relaxation to train wrecks that are still settling down to mature objects. And (2) we do not have comparably detailed studies of galaxies at high z that have gas fractions ≳ 50%. It is possible that mergers behave differently for such objects.
4.1.7. The Problem of Giant, Pure-Disk Galaxies: Conclusion
My most important suggestion in this section is that the modeling community relies too strongly on feedback as the only way to prune excessive bulge formation. On the contrary, I suggest that environmental differences in the amount of dynamical violence in galaxy formation histories are the central factor. I suggest that the solution is not a to whittle away the low-angular-momentum tail of the distribution of angular momenta in forming galaxies. Nearby galaxies dramatically show us the importance of violent relaxation. To me, the issue is: How much does violent relaxation dominate? How much is the evolution controlled by gentle accretion? And how do the answers depend on environment?