


The study of the intrinsic shape of bulges presents similarities, advantages, and drawbacks with respect to that of elliptical galaxies. Bulges are ellipsoidal systems located in the centre of disc galaxies, thus, the main drawback with respect to elliptical galaxies is that their analysis requires the isolation of their light distributions from other structural galaxy components. However, it is worth noting that a similar problem is faced in elliptical galaxies when defining a characteristic radius to measure the global axis ratio of the galaxy (Fasano & Vio, 1991). The most common approach to identifying a global axis ratio for the bulge is by performing a photometric decomposition of the galaxy surface-brightness distribution. In this method, the galaxy light is usually modelled as the sum of the contributions from the different structural components, i.e., bulge and disc, and eventually lenses, bars, spiral arms, and rings (Prieto et al., 2001, Laurikainen, Salo & Buta, 2005). A number of two-dimensional parametric decomposition techniques have been developed to this aim, such as: GIM2D (Simard, 1998), GALFIT (Peng et al., 2002), BUDDA (de Souza, Gadotti & dos Anjos, 2004), GASP2D (Méndez-Abreu et al., 2008a), GALPHAT (Yoon, Weinberg & Katz, 2011), or IMFIT (Erwin, 2015). On the other hand, the main drawback on the study of galaxy bulges, i.e., the presence of other components such as the main disc, represents in turn the main advantage. The presence of the galactic disc allows for accurately constraining the inclination of the galaxy. Hence, under the assumption that the two components share the same polar axis (i.e., the equatorial plane of the disc coincides with that of the bulge) it allows for the determination of the inclination of the bulge. This is crucial to solve one of the main concerns when dealing with elliptical galaxies.
Galaxy bulges were initially thought as axisymmetric ellipsoids placed at the centre of disc galaxies. The first piece of photometric evidence against this idea was given by Lindblad (1956). He showed a misalignment between the major axes of the disc and bulge in M31, realising that this would be impossible if both the disc and bulge were oblate. This photometric misalignment is similar to the isophote twist observed in elliptical galaxies and used as an indication of triaxiality in these systems (Williams & Schwarzschild, 1979). The extensive study undergone by Kent (1984) showed that the twisting isophotes between the central and outer parts of disc galaxies are quite common, but it was not until 1986 when Zaritsky & Lo (1986) properly studied the deviations from axisymmetry in the bulges of spiral galaxies. They found bulge-to-disc misalignments in their sample of 11 spiral galaxies hence confirming the high incidence of non-axisymmetric bulges in ordinary spirals and placing some parallelisms with elliptical galaxies. Beckman et al. (1991) also found compelling photometric evidence for triaxiality in the bulge of NGC 4736.
The first quantitative estimation of the intrinsic 3D shape of galaxy bulges using a statistical approach was performed by Bertola, Vietri & Zeilinger (1991). They measured the bulge AARD and the misalignments between the major axes of the bulge and disc in a sample 32 S0–Sb galaxies. Under the hypothesis that discs are circular, they found that these bulges are triaxial with mean axial ratios ⟨ Q ⟩ = 0.86 and ⟨ F ⟩ = 0.65. Interestingly, they also demonstrated that a random projection of the probability distribution function of the bulges axis ratios fit sufficiently well to the AARD of the elliptical galaxies presented in Binney & de Vaucouleurs (1981). The results were interpreted as both populations of objects having the same origin.
Fathi & Peletier (2003) derived the intrinsic ellipticity of bulges by analysing the deprojected apparent axis ratio of the galaxy isophotes within the bulge radius. This work did not assume any geometrical model for the galaxy but only that the disc be circular. They found ⟨ Q ⟩ = 0.79 and ⟨ Q ⟩ = 0.71 for the bulges of 35 early-type and 35 late-type disc galaxies, respectively. Despite the different methodologies, these results were in good agreement with previous results by Bertola, Vietri & Zeilinger (1991). Along the same lines, none of the 21 disc galaxies with morphological types between S0 and Sab studied by Noordermeer & van der Hulst (2007) harbours a truly spherical bulge. They reach this conclusion by assuming bulges to be oblate ellipsoids and comparing the isophotal axis ratio in the bulge-dominated region to that measured in the disc-dominated region. A mean flattening ⟨ F ⟩ = 0.55 was obtained which is slightly lower than the value found by Bertola, Vietri & Zeilinger (1991).
The number of galaxy bulges under study increased by an order of magnitude with the work of Méndez-Abreu et al. (2008a). They measured the structural parameters of bulges and discs of a sample of 148 early-to-intermediate spiral galaxies using a 2D photometric decomposition. They computed the probability distribution function of the intrinsic ellipticity from the bulges AARD, disc ellipticities, and misalignments between bulges and discs position angles. They suggested that about 80% of the sample bulges are triaxial ellipsoids with a mean axial ratio ⟨ B / A ⟩ = 0.85, confirming that bulges are slightly triaxial structures.
The vertical extension of galaxy bulges remains usually hidden from observations except for edge-on galaxies. Mosenkov, Sotnikova & Reshetnikov (2010) obtained a median value of the flattening ⟨ F ⟩ = 0.63 for a sample of both early- and late-type edge-on galaxies using near infrared photometry. These results match well with the early findings by Bertola, Vietri & Zeilinger (1991).
As well as for elliptical galaxies a number of works have attempted to quantify the intrinsic shape of individual bulges using only photometric data. The pioneering work of Varela, Munoz-Tunon & Simmoneau (1996) used a combination of geometrical deprojection and photometric inversion to work out the actual shape of the galaxy bulge in NGC 2841. They found that a family of triaxial ellipsoids with variable axis ratios is necessary to explain the photometric properties of its bulge. In 1998, Simonneau, Varela & Munoz-Tunon (1998) derived a set of equations defining the three intrinsic axes of a triaxial ellipsoid as a function of the measured geometry of a galaxy bulge and disc (axis ratios and position angles) and the unknown Euler angle φ (see Sect. 2 for definition). This seminal paper promoted the work of Méndez-Abreu et al. (2010). They introduced a new method to derive the intrinsic shape of bulges based upon the analytical relations between the observed and intrinsic shapes of bulges and their surrounding discs. Using the equations derived in Simonneau, Varela & Munoz-Tunon (1998) and introducing physical constraints on the accessible viewing angles, they found the following relation between the intrinsic semi-axes of the bulge and their observed properties
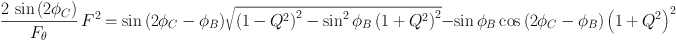 |
(9) |
where φB, φC and Fθ are functions of the observed quantities a, b, δ, and θ, see equations 12, 13, and 43 of Méndez-Abreu et al. (2010). Therefore, Eq. 9 directly relates the intrinsic 3D shape of the bulge with its observed properties. Unfortunately, the relation between the intrinsic and projected variables also depends on the spatial position of the bulge with respect to the disc on its own reference system (i.e., on the φ angle) and therefore, as well as for ellipticals, a deterministic solution of the problem cannot be given. However, the statistical analysis provided in Méndez-Abreu et al. (2010) allows us to obtain the probability distribution function of both semi-axis ratios, Q and F, for every single bulge, thus imposing tight constraints on its actual shape. Applying this technique to the sample of bulges presented in Méndez-Abreu et al. (2008a) they found a bimodal distribution of the triaxiality parameter (Figure 4, left panel). In particular, bulges with Sérsic index n ≤ 2 exhibit a larger fraction of oblate axisymmetric (or nearly axisymmetric) bulges, a smaller fraction of triaxial bulges, and fewer prolate axisymmetric (or nearly axisymmetric) bulges with respect to bulges with n > 2. Despite no correlations being found between the intrinsic shape of bulges and other properties such as bulge luminosity or velocity dispersion, the differences with the bulge surface-brightness distribution hint towards the presence of different bulge populations as suggested by Kormendy & Kennicutt (2004).
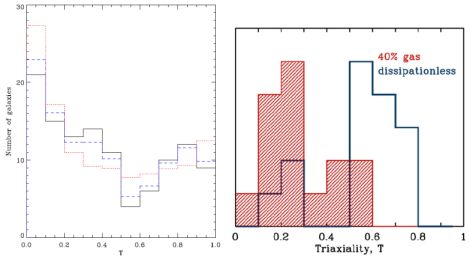 |
Figure 4. Composite figure showing the similar bimodal distribution of triaxiality parameters from observations (left panel) and simulations (right panel). Left panel: distribution of the triaxiality parameter T obtained from the sample of Méndez-Abreu et al. (2010) (continuous line) and for a simulated sample with both 30% and 100% of bulges hosting a nuclear bar (dashed and dotted lines), respectively. Extracted from Méndez-Abreu et al. (2010). Reproduced with permission from Astronomy & Astrophysics, ⓒ ESO. Right panel: distribution of both dissipational (hatched histogram) and dissipationless (solid line) mergers remnant triaxiality parameter from Cox et al. (2006). In both panels oblate galaxies have T = 0, prolate galaxies have T = 1, and all values in between are triaxial. Extracted from Cox et al. (2006). Reproduced with permission, ⓒ AAS. |
4.2. Evidences of triaxiality from kinematic measurements
Early kinematic studies of galaxy bulges were shown to rotate more rapidly than elliptical galaxies (Kormendy & Illingworth, 1982). In fact, the kinematic properties of many bulges are well described by dynamical models of oblate ellipsoids which are flattened by rotation with little or no anisotropy (Davies & Illingworth, 1983, Jarvis & Freeman, 1985, Fillmore, 1986, Corsini et al., 1999, Pignatelli et al., 2001). However, there are also kinematic evidences supporting a triaxial shape in a non-negligible fraction of these bulges. In 1989, two independent works of Bertola, Zeilinger & Rubin (1989) and Gerhard, Vietri & Kent (1989) reached the same conclusion about the triaxial bulge of the Sa galaxy NGC 4845. Using a combination of photometric and kinematic measurements they restrict the intrinsic axis ratio of its bulge to Q = 0.74 and F = 0.6. Their works were mainly supported by the presence of non-circular gas-motions in the galaxy centre. In a non-axisymmetric potential, the shape of the rotation curve will depend on the position of the LOS and the major axis of the non-axisymmetric component. A slowly rising rotation curve or one in which a bump of extreme velocities is seen near the centre are indications of triaxiality (Gerhard, Vietri & Kent, 1989). Based on these considerations, and building on the early work of Lindblad (1956), Berman (2001) demonstrated the presence of a triaxial bulge in the Andromeda galaxy (M31) by using a hydrodynamical simulation to match the observed properties of the galaxy. Further evidences for non-circular gas motion in galaxy centres can be found in Falcón-Barroso et al. (2006) and Pizzella et al. (2008). Other kinematic evidence for the existence of triaxial bulges comes from the presence of velocity gradients along the galaxy minor axis. Corsini et al. (2003) found minor axis rotation in 80% of their early-type spiral sample. In a series of papers, Coccato et al. (2004), Coccato et al. (2005) found that 60% of the unbarred galaxies show a remarkable gas velocity gradient along their optical minor axis. This was achieved by combining their own data with that present in the literature (Revised Shapley-Ames Catalog of Bright Galaxies) (Sandage & Tammann, 1981).
Despite the importance of adding kinematic information to determine the intrinsic shape of the bulges, and contrary to the works on elliptical galaxies (e.g., Statler, 1994a), there is not a well-established methodology to quantify the degree of triaxiality of bulges using the combined photometric and kinematic information, yet.
Polar bulges, as well as their analogous polar rings (Whitmore et al., 1990), are elongated structures perpendicular to the plane of the galaxy disc. A common signature of both the orthogonally decoupled bulge systems and the polar ring galaxies is that both contain a structural component whose angular momentum vector is roughly parallel to the major axis of the host galaxy.
Vertical elongation is not a common feature of bulges. Indeed, most bulges can be assumed to be flattened by rotation (see Sect. 4.2). Furthermore, orthogonally decoupled bulges are usually not even allowed in most statistical works since the condition A > B > C is commonly used, see Bertola, Vietri & Zeilinger (1991). Méndez-Abreu et al. (2010) relaxed this condition and found that only 18% of the observed bulges have a probability > 50% of being elongated along the polar axis with no bulges reaching a probability > 90%. In fact, to date NGC 4698 (Bertola et al., 1999), NGC 4672 (Sarzi et al., 2000), and UGC 10043 (Matthews & de Grijs, 2004) are the only spiral galaxies known to host a prominent bulge sticking out from the plane of the disc.
The case of NGC 4698 is particularly intriguing since it hosts also a polar nuclear stellar disc aligned with its polar bulge and thus perpendicular to the main disc. This galaxy was recently revisited by Corsini et al. (2012) and its intrinsic shape was derived using the methodology proposed by Méndez-Abreu et al. (2010). They found a slightly triaxial polar bulge elongated along the vertical direction with axis ratios Q = 0.95 and F = 1.60. This result agrees well with the observed kinematics presented in Bertola et al. (1999) and with a model where the nuclear disc is the end result of the acquisition of external gas by the pre-existing triaxial bulge on the principal plane perpendicular to its shortest axis and perpendicular to the main disc of the galaxy.