


Before address the complications of gas dynamics on the angular momentum acquisition of galaxies, let us review the theoretical picture for the origin of angular momentum in dark matter halos in which galaxies are embedded. We will begin by briefly discussing some the general characteristics of the spin of dark matter halos as derived from cosmological dissipationless N–body simulations, before reviewing the tidal torque model in § 2.1, and the role of major and minor mergers in angular momentum acquisition in § 2.2.
Within the framework of LCDM, the universe forms hierarchically, with less massive dark matter halos forming first, and halos merging together to form more massive halos over time (e.g., Peebles, 1982, Blumenthal et al., 1984, Davis et al., 1985). In this paradigm, since dark matter dominates the matter density of the universe, galaxies are expected to reside within the centers of massive dark matter halos. Thus, an important starting point for understanding the angular momentum of galaxies is to determine the angular momentum of dark matter halos in which galaxies reside, typically characterized by the dimensionless spin parameter (Peebles, 1969),
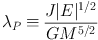 |
(1) |
or by the revised version of the spin parameter, first presented by Bullock et al. (2001), rewritten in terms of a dark matter halo's radius and virial velocity 1:
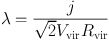 |
(2) |
where j = J / M is the magnitude of the specific angular momentum of the halo, Vvir = √GMvir / Rvir is the circular velocity at the halo virial radius, and Rvir and Mvir are the halo virial radius and virial mass, respectively.
Remarkably, a long history of studies of N-body simulations reveal that the spin parameters of dark matter halos do not show substantial trends with halo mass, redshift, or environment, (e.g. Fall & Efstathiou, 1980, Barnes & Efstathiou, 1987, Bullock et al., 2001, Vitvitska et al., 2002, Bett et al., 2007, Macciò et al., 2007, Berta et al., 2008, Bett et al., 2010), which is a natural result of the expectations of Tidal Torque Theory as the origin of dark halo angular momentum (see § 2.1, below). Instead, the distribution of halo spins from a number of simulations demonstrate a relatively good fit to a log–normal distribution:
 |
(3) |
with the distribution peaking at λ0 ≃ 0.035 with a Gaussian width of σ ≃ 0.5. For comparison, examples of best–fit parameters to this lognormal distribution from Bullock et al. (2001), Bett et al. (2007), Knebe & Power (2008), Ishiyama et al. (2013) and Zjupa & Springel (2016) 2, across a wide range in dark matter halo masses, are shown in Figure 1, showing remarkable agreement among simulations. The mass distributions of angular momentum within dark matter halos has also been shown to fit a universal two–parameter angular momentum profile (Bullock et al., 2001), based on the halo spin parameter as well as a halo shape parameter, though the underlying reason dark matter halos should be fit to a nearly universal angular momentum distribution profile is still not well understood.
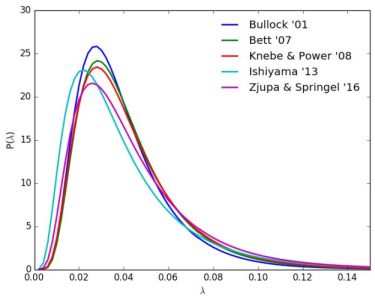 |
Figure 1. Distributions of dark matter halo spin parameters from Bullock et al. (2001), Bett et al. (2007), Knebe & Power (2008), Ishiyama et al. (2013) and Zjupa & Springel (2016). Shown here are the best fits to a the log–normal function defined in Equation 3. Quantitative details vary among of the simulation (based on, e.g., variations in the definition of the dark matter halo virial radius). However, there is good agreement among simulations, with best–fit parameters λ0 ≃ 0.035 and σ ≃ 0.5. |
The foundational picture of the origin of angular momentum in large scale structures (such as galaxies and dark matter halo)s is provided by Tidal Torque Theory (TTT, e.g., Hoyle, 1949, Peebles, 1969, Sciama, 1955, Doroshkevich, 1970, White, 1984, Barnes & Efstathiou, 1987). In TTT (for a more thorough recent review, see Schäfer, 2009), until the initial density perturbations in the universe reach maximum expansion (turnaround), their angular momentum grows linearly with cosmic time as a consequence of the torques exerted by the tidal gravitational fields from neighboring overdensities. After turnaround, structures decouple from the Hubble Flow and these overdensities collapse and virialize, conserving angular momentum in the process, such that the angular momentum of individual halos may be predicted (within an order of magnitude) by the initial large–scale gravitational tidal torques before maximum expansion. However, detailed analysis requires the inclusion of non–linear effects after turnaround, and thus is typically carried out by cosmological N–body simulations.
Under TTT, the total angular momentum acquired by a halo of a given mass at turnaround is expected to scale as L ∝ M5/3 (Peebles, 1969), with more massive halos acquiring more angular momentum, in part because it takes a long time for more massive halos to reach turnaround and decouple from the Hubble expansion. Taken in combination with the definition of the halo spin parameter in Equation 2, in which λ ∝ J / MVR, as well as the virial scaling relations V ∝ (M / R)1/2 and R ∝ M1/3, one straightforward expectation from TTT is that the halo spin parameter should be independent of halo mass (and redshift, as long as the redshift in question is after turnaround). This expectation of TTT has been well tested in a number of numerical studies using cosmological N-body simulations of large scale structure, and is foundational to numerous semi–analytic models of galaxy formation (see § 3.1), however, the importance of non–linear effects also lead to a number of quantitative disagreement between TTT and N-body simulations; for example, linear spatial correlations between the spins of halos on scales greater than about 1 Mpc are over-predicted in TTT by ∼50−70% compared to simulations (e.g., Porciani et al., 2002a, Porciani et al., 2002b).
More recently, Codis et al. (2012) and Codis et al. (2015) revisited the framework of TTT, emphasizing the importance of the anisotropic geometry of walls and filaments in the cosmic web. They found that the alignment direction of angular momentum in dark matter halos is dependent on the geometry of the cosmic web. The misalignments of accretion flows in the walls that collapse into filaments result in spin directions aligned with filaments for low mass halos. However, higher mass halos are strongly influenced by accretion (including mergers) that flow along these filaments, resulting in spin directions that are perpendicular to the filament. (This will be an important theoretical framework to keep in mind as we discuss revisions to the canonical picture of angular momentum acquisition onto galaxies in § 4.)
2.2. Angular Momentum Acquisition via Mergers
N-body simulations (Vitvitska et al., 2002, Maller et al., 2002).
One useful way to conceptualize this approach in a complementary role to TTT (rather than a “competing” mechanism) is to consider that the initial large scale tidal torques serve as a means of establishing the tangential velocities of infalling satellite halos. Thus, rather than attempting to fully understand the role of tidal torques in setting the ultimate angular momentum of a dark matter halo, one may instead focus on the particular kinematics of infalling satellites over the accretion history of the halo, which are in turn determined by the gravitational torques from the initial tidal field.
Under the merger model, galaxy halos tend to show larger variation in spin parameter than predicted in TTT. Larger mergers contribute substantial angular momentum based on their orbital motion, leading to significant spikes in the spin parameter of a post–merger halo, typically followed by a steady decline in spin parameter during epochs of gradual smooth accretion. Since major mergers can lead to a significant redistribution of angular momentum, under this model the high end of the angular momentum distribution of a dark matter halo is largely determined by the orbital angular momentum of its last major merger, with minor mergers (presumably from random infall directions) tending to contribute to the low end of the distribution.
1 The revised spin parameter from Bullock et al. (2001) was first introduced as λ′, but for the purposes of our discussions in this chapter, we will drop the prime and adopt this revised spin parameter as simply λ. Back.
2 Since Zjupa & Springel (2016) does not provide fitting parameters to the modified λ′ from Bullock et al. (2001), we compare here with their SO–halo lognormal fit to λP from Peebles (1969), given in Equation 1, which appears qualitatively similar to their results for the Bullock definition, based on their Figure 9. Back.