


4.1.1. The Role of Plasma Instabilities
The Braginskii-MHD equations outlined in Section 3.1 do not have an explicit dependence on the Larmor radius; it is simply assumed to be much smaller than the mean free path. However, a number of recent works have shown that the effects of a finite-Larmor radius may be relevant on larger scales in the ICM. In particular, when the pressure anisotropy violates the approximate inequalities
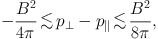 |
(4.1) |
a situation which is expected to occur readily in the cluster plasma (Schekochihin et al. 2005, Lyutikov 2007, Kunz et al. 2011), rapidly growing Larmor-scale instabilities (namely, the firehose instability on the left side of the equation and the mirror instability on the right side) are triggered and act to regulate the pressure anisotropy back to within its stability boundaries. The effect of these microscale instabilities on the pressure anisotropy and, conversely, the transport of momentum, is an open question.
Collisionless kinetic simulations of the driven firehose instability (e.g., Matteini et al. 2006, Hellinger & Trávníček 2008, Kunz et al. 2014) have shown that the collisionality of the plasma, supplemented by the anomalous scattering of particles off the microscale fluctuations, adjusts to maintain a marginally firehose-stable pressure anisotropy. This effectively reduces the parallel viscosity of the plasma, making it possible for KHI to develop more easily at surfaces like cold fronts. In addition, with the pressure anisotropy microphysically pinned at the firehose stability threshold (the left inequality of Equation 4.1), the resulting viscous stress would effectively cancel the magnetic tension, again easing development of KHI. In the case of the mirror instability (see Kunz et al. 2014, Riquelme et al. 2014), the pressure anisotropy appears to be regulated not just by anomalous particle scattering but also by an increasing population of resonant particles becoming trapped in magnetic mirrors where the pressure is naturally less anisotropic.
Consideration of these plasma effects requires choices to be made when employing the Braginskii-MHD equations in simulations of cold fronts. In such simulations, when the pressure anisotropy exceeds the bounds of Equation 4.1, these instabilities will be triggered, but since the Larmor radius is severely underresolved, they will occur on the smallest scale available, that of the cell size. The effects of the instabilities will then be damped out by the numerical diffusivity associated with the grid scale. Alternatively, as suggested by the kinetic simulations, the pressure anisotropy may be limited within the bounds suggested by Equation 4.1, which amounts to an increase of the parallel Reynolds number of the ICM.
In regions near cold fronts, these effects may not be of significant concern, as the magnetic field is amplified to near-equipartition scales, and the boundaries in Equation 4.1 will be more difficult to transgress. However, future simulation studies of cold fronts using the Braginskii-MHD equations should investigate the potentially observable effects on cold fronts of limiting the pressure anisotropy or not.
4.1.2. Distinguishing Between the Effects of Magnetic Fields and Viscosity
All of the cold front simulations we have detailed in this review have shown that magnetic fields and viscosity are both capable of suppressing KHI at cold front surfaces, provided that their effects are strong enough. The question then remains as to which effect is most responsible for this suppression in the cold fronts that lack evidence of KHI. Does one effect dominate over another, or are both effects important?
The major difficulty in answering this question are the lack of strong independent constraints on either effect apart from the lack of KHI at cold fronts itself. From the observational side, we do not currently have an independent check on the strength of the magnetic field in the layer at the cold front surface. In principle, an estimate of the field strength along the line of sight could be made using RM observations in the vicinity of the front. However, the strength of this component may or may not be comparable to the orthogonal component in the plane of the sky where the cold fronts are being observed, especially if the latter component is increased by shear amplification and/or draping effects at the front surface.
The most promising way to constrain the magnetic field strength in the layer would be to observe a deficit in the thermal pressure at a front surface, providing an essentially direct measurement of the magnetic pressure at that location, since the sum of the thermal and magnetic pressures should be continuous, provided the measurement is made on the side of the front where the magnetized layer is located. This would be easiest to check in sloshing cold fronts, which are isobaric across the front surface. Recently, Reiss & Keshet (2014) used deprojected pressure profiles across a number of sloshing cold fronts from the literature and found that many of the fronts in their sample have pressure discontinuties consistent with the existence of enhanced magnetic pressure underneath the front surface. The average ratio of thermal to total pressure in these regions was ξ ≃ 0.8, which implies ∼20% of the total pressure is in the form of magnetic fields. The average value is statistically significant, though for many of the cold fronts in their sample the significance is modest (up to a few σ). They also did not examine the characteristics of each individual front in detail to determine if the presumed magnetization in that front would be sufficient to prevent the development of KHI. However, these initial results are promising, and deserve future study and longer exposures by Chandra.
For the viscosity, if we assume its origin is tied to the ion collisions in the ICM, it will have the Spitzer form (Equation 3.9), which can be easily determined from the plasma properties. However, the effective viscosity within a small region will be dependent on the magnetic field direction, and as noted in the previous section there are still large theoretical uncertainties regarding the effect of microscale plasma instabilities on the collisionality of the plasma.
To break this apparent degeneracy between magnetic fields and viscosity, simulations should investigate other aspects of the cold fronts and their near vicinity and make predictions for what observable effects may arise from either aside from the suppression of KHI. For example, R13 showed in their unmagnetized simulations of the sloshing cold fronts in Virgo that in the absence of viscosity, the cold gas underneath the front surface should exhibit multiple edges in surface brightness as seen in projection. These edges are absent if the plasma is viscous. It is not yet known whether the same features would be present in a cold front with a magnetized layer. In the context of remnant-core cold fronts, the characteristics of the edges of the cold front and the stripped tail and wake of the subcluster explored in detail by R15A and R15B may be compared to otherwise identical simulations with magnetic fields to determine which effect best matches the observations.
4.1.3. How Efficient is Thermal Conduction in the ICM?
As detailed in Section 3.5, MHD simulations of cold fronts with anisotropic thermal conduction have given mixed results as to whether or not magnetic fields can effectively protect the sharp density and temperature jumps from being smeared out by an efficient thermal conductivity. In the simulations reviewed here, magnetic fields seem to largely prevent the sharp temperature and density gradients of remnant-core cold fronts from becoming smeared out due to conduction, but cannot do so in the case of sloshing cold fronts (though we again note as we did in Section 3.5 that the cold front jumps do appear to be somewhat smeared out by conduction in the S13 simulations; see Figures 19 and 24). Why is this the case?
Several factors may be at play. As noted above, the behavior of magnetic fields at the cold front surface is rather different in the case of remant-core cold fronts and sloshing cold fronts: in the former, the field is “draped” on the outside of the front, in the latter, the field is amplified by shear amplification on the inside of the front. The draping layers on the outside of the fronts tend to be more long-lasting in the simulations than the layers on the inside of the fronts, which are more transient (see Section 3.3). The geometry of the cold front is also an important consideration. In the Asai-MHD and S13 simulations, the magnetic field layer appears to wrap essentially all the way around the cold front, strongly restricting conductive heat flux across the interface. As noted above, in the sloshing simulations of Z13 and Z15, tangling of field lines along the front surface by KHI and the presence of other regions of hot gas which are connected to the cold gas by magnetic fields permit a flux of heat to the cold phase. However, the KHI in these simulations were able to develop due to the initial magnetic field strength being set by β = 400/1000 (Z13/Z15); in a more strongly initially magnetized simulation (β ≲ 100), the draping layers may have been more effective.
It should also be noted that the remnant-core cold front simulations from the Asai-MHD and S13 works have poorer resolution (∼7-10 kpc, in the 3D simulations) than the sloshing cold front simulations by ZuHone (∼1-2 kpc). The lower-resolution simulations have higher numerical dissipation, preventing some KHI modes from growing and limiting the development of turbulence, both of which could re-tangle magnetic field lines if they were not strong enough to prevent the growth of either effect in the first place. For these reasons, the remnant-core scenario with anisotropic thermal conduction should be re-examined at higher resolution.
The question of whether or not the narrow widths of cold front interfaces are even compatible with anisotropic thermal conduction is important for the study of the thermodynamic properties of the ICM as a whole. A considerable amount of attention in recent years has been devoted to the effect of anisotropic thermal conduction on the stability properties of the ICM. In the classical picture, the ICM is convectively stable since the entropy in clusters is stratified with dS / dr > 0. However, a number of studies (Balbus 2000, Balbus 2001, Parrish & Quataert 2008, Parrish et al. 2008, Quataert 2008, Bogdanović et al. 2009, Parrish et al. 2009) have demonstrated that with efficient thermal conductivity in the ICM, the entire cluster atmosphere is unstable to convection provided that dT / dr ≠ 0, which is observed to be true for nearly all clusters, especially those with cool cores (though other works have emphasized that these instabilites are affected strongly by the inclusion of Braginskii viscosity; see Kunz et al. 2011, 2012). Other works have emphasized the possible role of thermal conduction in setting the temperature profiles of clusters (Zakamska & Narayan 2003, Guo et al. 2008, McCourt et al. 2013), partially offsetting cooling in cores (Bertschinger & Meiksin 1986, Bregman & David 1988, Ruszkowski & Begelman 2002, Kim & Narayan 2003, Voigt & Fabian 2004, Parrish et al. 2010, Ruszkowski & Oh 2010, Ruszkowski & Oh 2011), and influencing the condensation of multiphase gas in cluster cores and giant elliptical galaxies (Sharma et al. 2012, McCourt et al. 2012, Wagh et al. 2014, Voit & Donahue 2015, Voit et al. 2015, Yang & Reynolds 2015). Therefore, determining if cold fronts demonstrate that the thermal conductivity in the ICM is very low would have a significant impact on our understanding of the thermodynamics of the cluster core. Such a suppression of thermal conductivity has been suggested by previous theoretical studies, either due to strong curvature of magnetic field lines at small scales or by microscale plasma instabilities (Chandran et al. 1999, Malyshkin & Kulsrud 2001, Narayan & Medvedev 2001, Schekochihin et al. 2008).
More observations are needed to increase the number of cold front observations with high-quality, long-exposure images and spectra for simulations to compare against. To best constrain the plasma properties, observations of nearby clusters with Chandra are most useful. For instance, other portions of the largest Virgo cold front than the one observed by Werner et al. (2016) should also be observed with similar exposure (∼ 500 ks). Simulations predict (R13) that the velocity shear may change along the length of the front, indicating that the magnetic field strength in the layer and/or the presence of KHI may be different at other locations along the front.
An important leap forward in the use of cold fronts for studying the physics of the cluster plasma will be provided by the next generation of X-ray observatories, which will have effective areas that far surpass what is currently available. There is no doubt that the increased effective area of Athena (Nandra et al. 2013), with over an order of magnitude improvement in area over that of current instruments, will greatly improve the statistics of measuring the temperature on either side of cold fronts, but this improvement will be blunted by the poorer spatial resolution of Athena (∼ 5") with respect to Chandra’s superb sub-arcsecond resolution. The mission concept X-ray Surveyor (Weisskopf et al. 2015) would provide both a similar increase in effective area, coupled with Chandra-like spatial resolution.
The next generation of X-ray observatories will also possess high resolution microcalorimeters which will be able to measure the properties of the velocity field of the ICM from the shifting and broadening of emission lines in the X-ray spectrum. The first such mission will be Astro-H (Takahashi et al. 2014), to be launched in early 2016. A recent study carried out by ZuHone et al. (2015b) used synthetic observations to show that Astro-H will be able to measure the basic kinematic properties of sloshing cold fronts, namely the shift of the spectral lines produced by the bulk motion of the sloshing gas (provided that our line of sight is at least partially within the sloshing plane) and the line broadening produced by the variation in this bulk motion and sloshing-driven turbulence. Unfortunately, they also showed that due to Astro-H's poor spatial resolution of ∼1’, it will be unable to place any meaningful constraints on the ICM viscosity from studies of cold fronts. Meaningful constraints on the cluster plasma from kinematics will require a mission with both high spatial and spectral resolution, such as Athena, or (more likely) X-ray Surveyor, both of which will have calorimeters with spectral resolution equivalent to or higher than Astro-H.