Annu. Rev. Astron. Astrophys. 2015. 53:115-154 Copyright © 2015 by Annual Reviews. All rights reserved

6. THE SMBH – BULGE MASS RELATION

In the Introduction we noted the observed proportionality (1) between M and M_b as well as the M − σ relation. So far we have concentrated almost entirely on the second of these relations, and suggested that it arises because the black hole feedback itself directly limits the mass reservoir available for black–hole growth. Quite independently of details, almost every discussion of this relation adopts this view (see Section 7 below).

But the character of the M − M_b relation must be very different. Since we are assuming that feedback ensures that the black hole mass M is set by σ we cannot argue that M is independently set by M_b. But reversing the argument to suggest that the black hole mass M sets M_b is also implausible, since M_b is in the form of stars.

So there can be no directly causal connection between the black hole mass M and the stellar bulge mass M_b. (Indeed one view – see Section 6.3 below – asserts that the connection is purely statistical.) Instead, their relation must arise because whatever determines M_b makes it proportional to σ⁴. Empirically, we already know that this is approximately true, at least for elliptical galaxies, the largest spheroids of all, because these are observed to obey the Faber–Jackson (1976) relation

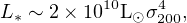(68)

Here L_* is the total stellar luminosity and mass of an elliptical, so for mass–to–light ratios ∼ 5 we immediately get the stellar mass as

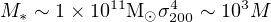(69)

There is now general agreement that this relation, like the M−σ relation, may result from feedback inhibiting and ultimately suppressing the process that produces it. The difference is that here the feedback is from stars, and what ultimately has to be suppressed is star formation. Several papers make this point, starting with Murray et al. (2005). Power et al. (2011) show that this approach gives a bulge stellar mass

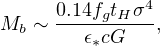(70)

where є∗ ≃ 2 × 10⁻³ measures the total luminous energy yield from a main–sequence star in terms of its rest–mass energy M_∗ c², and t_H is the Hubble time. Comparing with (39) we get

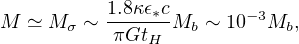(71)

which is similar to observational estimates (cf equation 1). Both the M − σ and the M − M_b relations hold for elliptical galaxies, so equation (70) automatically reproduces the Faber–Jackson (1976) relation for typical mass–to–light ratios. In this view, the similarity of the SMBH and stellar (Faber–Jackson) M, M_b ∝ σ⁴ relations (2, 69) follows directly because both result from momentum feedback, and the ratio M / M_b ∼ 10⁻³ reflects the relative efficiencies of the black hole and stellar versions.

6.2. The M − σ relation for Nucleated Galaxies

A similar argument (McLaughlin et al. 2006) shows that for nucleated galaxies (i.e those whose central regions are dominated by nuclear star clusters, with no detectable sign of the presence of a supermassive black hole) there should be an offset M − σ relation between the mass of the cluster and the velocity dispersion, i.e.

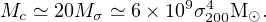(72)

Typically these galaxies are small, with σ < 120 km s⁻¹. The factor ∼ 20 offset in cluster mass for a given σ arises because momentum–driving by an ensemble of cluster stars is about 20 times less efficient per unit mass than from a black hole accreting at the Eddington rate.

6.3. Mergers and the M − M_b relation

Jahnke & Macciò (2011) offer a radically different interpretation of the M − M_b relation. Building on earlier work of Peng (2007) they assume that black hole and bulge masses are built up by repeated mergers of smaller galaxies with uncorrelated M and M_b. They follow this evolution using dark matter halo merger trees, and as a result of the central limit theorem find that M is roughly proportional to M_b, with the scatter decreasing for larger masses, where there have been more mergers. They conclude that the SMBH - bulge scaling relation may have an explanation that is largely or even entirely non–causal.

But it is hard to accept that there is no more physics in the SMBH scaling relations than this. First, the actual ratio M / M_b is left undetermined by this procedure. Second, to get from the M − M_b relation to M − σ requires one to assume something like the M_b ∝ σ⁴ relation (69) implied by Faber–Jackson, so physics presumably must enter here too (cf the subsection above). Finally, it would seem a remarkable coincidence that the outcome of this indirect process by chance produces an M − σ relation exactly equivalent to requiring that the SMBH Eddington thrust should just balance the weight of the bulge gas.