


2.3 The Singular Isothermal Sphere (SIS)
Galaxies and clusters of galaxies that act as
gravitational lenses can be approximated by
singular isothermal spheres. It is then easy to relate an
angular scaling parameter  E, referred to as the Einstein
radius, to the mass inside the corresponding
light cone. The Einstein radius
E, referred to as the Einstein
radius, to the mass inside the corresponding
light cone. The Einstein radius  E corresponds to the ring
image of a point source aligned exactly on the axis of
the lens (Fig. 7). For a singular
isothermal sphere the
line of sight velocity dispersion is constant as well as the
gradient of the projected potential. Therefore, the
deviation angle is constant and
E corresponds to the ring
image of a point source aligned exactly on the axis of
the lens (Fig. 7). For a singular
isothermal sphere the
line of sight velocity dispersion is constant as well as the
gradient of the projected potential. Therefore, the
deviation angle is constant and  E can be obtained from
the one dimensional velocity dispersion
E can be obtained from
the one dimensional velocity dispersion  1D as :
1D as :
and
The perfect alignment of the source on the optical axis
of the deflector is quite unlikely, but with a small
misalignment the observer will see two opposite arcs
approximately located at the Einstein radius (Fig. 7).
In fact, the total mass inside the radius 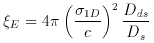
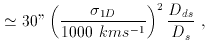
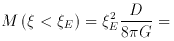
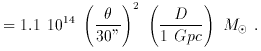
 E mostly depends
on the Einstein radius. More generally, the mass
inside the cone of light limited by a large arc will be a
robust parameter that does not depend strongly on the
actual mass distribution. Therefore, observations of arcs give
the possibility of quickly deriving the total gravitational mass
and the mass to light ratio of a cluster core without
any spectroscopic determination of the velocity
dispersion. It is worth noting that for real clusters both
methods of mass determination give results
which do not differ by more than 10% in
the cluster center
(Mellier 1993,
Mellier et al. 1994).
E mostly depends
on the Einstein radius. More generally, the mass
inside the cone of light limited by a large arc will be a
robust parameter that does not depend strongly on the
actual mass distribution. Therefore, observations of arcs give
the possibility of quickly deriving the total gravitational mass
and the mass to light ratio of a cluster core without
any spectroscopic determination of the velocity
dispersion. It is worth noting that for real clusters both
methods of mass determination give results
which do not differ by more than 10% in
the cluster center
(Mellier 1993,
Mellier et al. 1994).