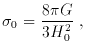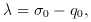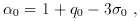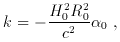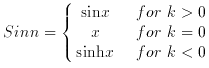Since the angular sizes of gravitational arc(let)s
depends on the cosmological distances of the
lens and sources, in principle arc(let)s can be used to
probe the geometry of the universe itself. With well-known
arc configurations it should be possible to determine the
cosmological parameters H0, and 
= 0 + 
0. In fact,
we are unable to separate the relative contribution of 0 and
0.
For the present time, we have some hope of measuring the mass density of the
universe, 0, from
independent observations, mainly from the large
scale structure velocity field. Therefore we should be
able to obtain a value for 0 = 1 - 0 if we adopt the
theoretical hypothesis of an inflation period for the primeval universe.
Additional observations of gravitational arcs may offer
an opportunity to get around this
hypothesis. In practice, a value of
would be obtained by comparing the relative astrometric positions of arc(let)s
predicted for various cosmological models with the observations.
Unfortunately the positions of arcs vary very little
with the cosmological parameter if its reduced value is not larger than
1., and we already know that it cannot be much larger
(Carroll, Press &
Turner 1992).
Also, the positions of arcs are far more
sensitive to the lens modeling. In conclusion, the determination of
will be done only
if an almost perfect modeling of the
lens is achieved and if very good astrometric positions of the arcs are
obtained. It will not be a surprise that this topic is still largely
speculative.
In the following we must indeed assume that the general theoretical framework given in part 2 is valid. Note that Nottale (1988) emphasized that giant arcs with known redshift can test gravitation theories on cosmological scales, provided dynamical masses and gravitational masses are identical. The present-day observations do not contradict the predictions of General Relativity, and actually confirm the equality between the two masses (Nottale 1988, Dar 1992).
The time delay which appears between the successive observations of an intrinsic event in the source in each multiple image of an arc system can be used to infer H0. The original idea was introduced for multiple quasars by Refsdal (1964) and applied to the double QSO 0957+561. It has not succeeded so far in providing a better value of H0 than other methods (see Kochanek 1991): observational discrepancies were reported between the radio and optical measurements of the time delay, and the modeling of the lens appears still more complex than previously thought with the discovery of a fold arc in the field of the associated cluster (Bernstein et. al 1993). At first glance, the observational situation would seem better for arcs. A-priori we expect a large number of supernovae events in distant blue galaxies which have a large star formation rate. The magnified event that appears at different times on each image can be well recognized. Giraud (1992b) claimed to detected a local surface brightness variation in the giant arc observed in MS0302+17 which could be interpreted as such supernovae explosion. But his detection is marginal and is not confirmed by similar observations done by other observers during almost the same period. However, even if it is possible to search for and monitor supernovae, the time delay can reach hundreds of years for separate multiple images! Very often, only for the region near the critical line of two merging arcs is the time delay a few days or weeks (Kovner & Paczynski 1988). But even if by chance a supernova were observed with such an ideal geometrical configuration, there will still remain an uncertainty in the determination of H0 associated with the modelling of the cluster lens, even if it could be better determined than for small galaxy lenses. It is likely that a reliable value of the Hubble constant will need multiple observations of supernovae in a large number of clusters with giant arcs; an observational challenge which will be out of reach for a long time.
Paczynski & Gorki
(1981)
first suggested using the multiple images of
a lensed quasar to constrain the cosmological constant provided the core
radius and the velocity dispersion of the lens are known (and obviously
the redshifts of the lens and the source). The technique
assumes a model for the mass profile which relates the angular
separation of split images to the velocity dispersion and the angular
diameter distances. In that case, it is straightforward to find the
best which is compatible with
the observations. Recently,
Breimer and Sanders
(1992)
used basically the same approach as
Paczynski & Gorki but on clusters with giant arcs. They discussed
simultaneously the gravitational lensing analysis and dynamical mass
distributions inferred from both the galaxy behavior and the distribution
of hot X-ray gas. They concluded that if light traces mass the observations
of A370 are compatible with
= 0. However, if light traces mass in a more complex way
(M/L varies with distance), a wide range of cosmologies
are also possible.
In a similar way, the cosmological parameters could be inferred by measuring the position and magnification of two arcs with different redshifts and observed in the same cluster. From equation (7) of section 2, the ratio of deviation angles generated by a singular isothermal sphere for two different sources with different redshifts is
and is independent of H0. Therefore, the ratio only
depends on the
curvature k (and the deceleration parameter q0)
and the cosmological constant
where
and
In principle this technique should work. However, the
ratio of the angular distances
between the two arcs is strongly dependent on the lens modeling and the
assumptions made for the sources. It is likely that this approach will
need the discovery of at least two relatively bright arcs with different
redshifts in a cluster
lens with a simple geometry and
better spectroscopic capabilities coming from future large telescopes.
:
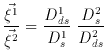
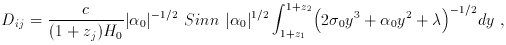(24)
