Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
The Friedman models
(44,
45)
were proposed as the simplest solutions
of Einstein's equations without the  -term. Robertson
(104) and
Walker
(121)
showed that global symmetry arguments of homogeneity and
isotropy lead to a spacetime geometry described by the line element
-term. Robertson
(104) and
Walker
(121)
showed that global symmetry arguments of homogeneity and
isotropy lead to a spacetime geometry described by the line element
For k = 0, the expression in parentheses describes the Euclidean
metric for three dimensional space in spherical polar coordinates. For
k = + 1, the three-space has the closed topology of the surface of a
hypersphere in four dimensions, whereas for k = - 1, the three-space
is open. The (r,
This function a (t) is determined by Einstein's equations if the
energy momentum tensor of the physical contents of the universe are
known. If
The second equation is none other than that of energy conservation
under adiabatic expansion.
The present state of the universe is matter-dominated in the sense
that bulk of the contribution to
The small component of radiation present today was, however, more
dominant in the past. This is because for radiation with the equation
of state
The microwave background radiation (MBR) energy density may be taken
as a close approximation to (
We may specify the redshift z of an epoch by the relation
Clearly 1 + zeq
At times t << teq (i.e. z >>
zeq), the radiation dominated over
matter, and we find that the function a (t) was approximately given by
(This presupposes the neglect of the curvature term
kc2 / a2 in Eq. 2 in
comparison with
where g denotes the effective degrees of freedom of relativistic
particles present in thermodynamic equilibrium at that
temperature. The number varies between a value of about 102
(at 1020 MeV) and 3 or so (at present).
Working backwards chronologically, there are three significant
epochs in the early universe. In the first epoch, electrons combined
with ions to form neutral atoms. The characteristic energy was the
binding energy (~ 13.6 eV) of the H-atom, and the temperature was
about 3000-4000 K. We denote this epoch by t =
tdec to indicate that
the radiation decoupled from matter in the absence of free electrons
as scatterers. During the second epoch, free neutrons and protons
combined to form light nuclei at temperatures between
108-109 K. In
the third epoch, that of the grand unified theories (GUTs), the
breakdown of grand-unification symmetry at energies of about
1014 GeV
led to the bifurcation of the electroweak interaction from the strong
interaction. For this t ~ 10-35 s. (There is also a
fourth epoch
preceding the GUTs epoch, prior to which the universe was governed by
the laws of quantum gravity. Known as the Planck epoch, it was at
tp ~
10-43 s. Classical general relativity could not be valid up to this
epoch.)
The third epoch, at temperatures around 1014 GeV, is of interest to
particle physicists. Some of the basic features of our
universe - e.g. the photon-to-baryon-number ratio, which is presently
observed to be (N
The confidence with which physicists extrapolate their discussions
to epochs as early as 10-35 s rests on the successes of the standard
hot big-bang model at the first two stages, namely the prediction of
relic abundances of light nuclei and the interpretation of MBR as the
relic radiation. The standard theory encounters many problems of a
fundamental nature, however, which require a radical rethinking of the
very early scenario. This was the motivation for introducing the
concept of inflation. Before considering the proposed remedy, it is
appropriate to take a look at the problems.
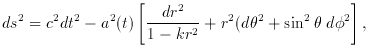
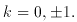
 ,
,  ) coordinates are the ``comoving
coordinates'' of a
typical ``fundamental observer'' who ``sees'' the universe as homogeneous
and isotropic. The proper time of such an observer is measured by t,
called the cosmic time, and the corresponding frame of reference is
called the cosmic rest frame. The function a (t) denotes
the typical
length scale of the universe and, for an expanding model, it is called
the expansion factor.
) coordinates are the ``comoving
coordinates'' of a
typical ``fundamental observer'' who ``sees'' the universe as homogeneous
and isotropic. The proper time of such an observer is measured by t,
called the cosmic time, and the corresponding frame of reference is
called the cosmic rest frame. The function a (t) denotes
the typical
length scale of the universe and, for an expanding model, it is called
the expansion factor.
 is the energy
density (
is the energy
density (
 c2) and
p the pressure of these
contents, these equations can be reduced to
c2) and
p the pressure of these
contents, these equations can be reduced to
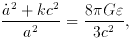
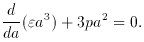
 comes from matter that is either at
rest in the cosmic rest frame or is moving slowly (compared to c)
relative to it. For such matter pm
comes from matter that is either at
rest in the cosmic rest frame or is moving slowly (compared to c)
relative to it. For such matter pm  0, and from Eq. 3 we get
0, and from Eq. 3 we get 
 a-3.
The simplest model of this kind is the flat model, for which
a-3.
The simplest model of this kind is the flat model, for which  m
m  (
( / a)2.
This leads therefore to a critical density
/ a)2.
This leads therefore to a critical density  c
c  2 x 10-29 h2
gcm-3 of the matter. For k = + 1 models,
2 x 10-29 h2
gcm-3 of the matter. For k = + 1 models,  >
>  c, whereas for
k = - 1
models,
c, whereas for
k = - 1
models,  <
<  c, In general
we write the density
c, In general
we write the density  as
as 
 c with
c with  > 1 for
k = 1,
> 1 for
k = 1,  < 1 for k = -1.
< 1 for k = -1.
 r = 3
pr, Eq. 3 gives
r = 3
pr, Eq. 3 gives  r
r  a-4. We denote by teq and
aeq
a-4. We denote by teq and
aeq  a (teq), the epoch and the expansion factor when
a (teq), the epoch and the expansion factor when  m =
m =  r. Clearly,
r. Clearly,
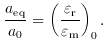
 r)0. A simple calculation gives
r)0. A simple calculation gives
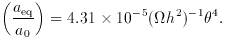
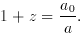
 2.3 x 104 (
2.3 x 104 ( h2)
h2)  -4; if we take
-4; if we take  mo
mo  3 x 10-31 gcm-3,
then zeq
3 x 10-31 gcm-3,
then zeq  103. This means that for z > zeq the
universe is
radiation-dominated, whereas for z < zeq
it is matter-dominated.
103. This means that for z > zeq the
universe is
radiation-dominated, whereas for z < zeq
it is matter-dominated.
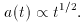
 / a. As
discussed below, this assumption is
nontrivial.) Since
/ a. As
discussed below, this assumption is
nontrivial.) Since 
 T4 for
radiation, it follows that T
T4 for
radiation, it follows that T  t-1/2. This
time-temperature relationship can be written, more quantitatively, as
t-1/2. This
time-temperature relationship can be written, more quantitatively, as

 / NB) = 3.52 x 107
(
/ NB) = 3.52 x 107
( h2)-1
h2)-1  3 - may have become frozen
in at this epoch. Discrete structures (galaxies, clusters,
superclusters, etc.) could conceivably grow from primordial seeds
going back to this epoch. (For reviews and discussions of some of
these problems, see
81,
84,
125).
3 - may have become frozen
in at this epoch. Discrete structures (galaxies, clusters,
superclusters, etc.) could conceivably grow from primordial seeds
going back to this epoch. (For reviews and discussions of some of
these problems, see
81,
84,
125).