Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
325-362 Copyright © 1991 by Annual Reviews. All rights reserved |
3.2 The Epicycles of Inflation
Since the inflationary idea seemed to be quite attractive, several mechanisms were devised by which this idea can be implemented. Each of these models has some advantages and disadvantages and none of them is completely satisfactory. We briefly highlight three models.
For the universe to expand exponentially, the energy density should
remain (at least approximately) constant. Various models of inflation
differ in the process by which this is achieved. In most of them the
quasi-constant energy density  (t) is derived from phase transition at
the GUTs epoch. Although in specific details one grand unified theory
may differ from another, almost all of them involve gauge theories
with a mediating role played by the Higgs scalar field
(t) is derived from phase transition at
the GUTs epoch. Although in specific details one grand unified theory
may differ from another, almost all of them involve gauge theories
with a mediating role played by the Higgs scalar field  . We need not
go into the intricacies of how
. We need not
go into the intricacies of how  is related to the other matter
fields. The feature of interest to us is that the potential energy
density V of the scalar field
is related to the other matter
fields. The feature of interest to us is that the potential energy
density V of the scalar field  depends on the ambient temperature T.
depends on the ambient temperature T.
At any given temperature T that is higher than a critical
temperature Tc, the minimum value of V is found
to be at the expected
zero of  . We may term this minimum
at
. We may term this minimum
at  = 0 as the vacuum state of
= 0 as the vacuum state of
 . As the temperature is lowered,
however, the minimum of V may no
longer remain at
. As the temperature is lowered,
however, the minimum of V may no
longer remain at  = 0 but may shift
to a finite value
= 0 but may shift
to a finite value  =
=  . This
phase transition occurs at T = Tc and may be
likened to the
condensation of steam. Thus
. This
phase transition occurs at T = Tc and may be
likened to the
condensation of steam. Thus  would
tend to transit from
would
tend to transit from  = 0 to
= 0 to  =
=  .
.
If  were to condense immediately at
Tc, all the excess energy could
be released at once. In the more likely case of supercooling, however,
were to condense immediately at
Tc, all the excess energy could
be released at once. In the more likely case of supercooling, however,
 may continue at
may continue at  = 0 and move to the true minimum
= 0 and move to the true minimum  =
=  later. During this transitional stage, the state
later. During this transitional stage, the state  = 0 is called the
false vacuum state, since the true vacuum is now at
= 0 is called the
false vacuum state, since the true vacuum is now at  =
=  . The
original model for the inflation, due to Guth
(48),
invoked this
temperature dependence of the potential energy of the Higgs field
V (
. The
original model for the inflation, due to Guth
(48),
invoked this
temperature dependence of the potential energy of the Higgs field
V ( , T). [The
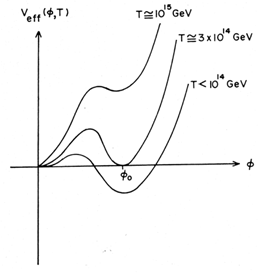
potential energy has the form shown in
Figure 3. Here Tc
, T). [The
potential energy has the form shown in
Figure 3. Here Tc  3 x 1014 GeV.]
3 x 1014 GeV.]
|
Figure 3. The potential energy of the Higgs
field |
At temperatures T >> Tc, the potential V
has only one minimum (at  =
0) with V(0)
=
0) with V(0)  (1014 GeV)4. As the temperature is lowered to
T ~ Tc, a
second minimum appears at
(1014 GeV)4. As the temperature is lowered to
T ~ Tc, a
second minimum appears at  =
=  . For T <<
Tc, the
. For T <<
Tc, the  =
=  minimum is the
``true'' minimum [i.e. V (
minimum is the
``true'' minimum [i.e. V ( )
)  0 << V
(0)]. Now consider what happens in
the early universe as matter cools through T
0 << V
(0)]. Now consider what happens in
the early universe as matter cools through T  Tc. At T
>> Tc, the
minimum configuration corresponds to
Tc. At T
>> Tc, the
minimum configuration corresponds to  = 0 whereas for T ~ Tc it is
= 0 whereas for T ~ Tc it is  =
=  . Matter in the universe does not instantaneously switch over from
. Matter in the universe does not instantaneously switch over from
 = 0 to
= 0 to  =
=  , however. The
universe can get ``stuck'' at
, however. The
universe can get ``stuck'' at  = 0 (the
false vacuum), with V = V (0), even at T <
Tc, and will expand
exponentially because the dominant energy density driving the
expansion is the constant V (0) - V (
= 0 (the
false vacuum), with V = V (0), even at T <
Tc, and will expand
exponentially because the dominant energy density driving the
expansion is the constant V (0) - V ( )
)  V (0). Over the course of time,
thermal fluctuations and quantum tunneling will induce a transition
from the false vacuum
V (0). Over the course of time,
thermal fluctuations and quantum tunneling will induce a transition
from the false vacuum  = 0 to the
true vacuum
= 0 to the
true vacuum  =
=  , thereby ending
the inflation in localized regions (``bubbles''). The phase transition
is expected to be completed by the expanding bubbles colliding,
coalescing, and reheating the matter.
, thereby ending
the inflation in localized regions (``bubbles''). The phase transition
is expected to be completed by the expanding bubbles colliding,
coalescing, and reheating the matter.
Detailed analysis, however, shows that this model does not work (50). In order to have sufficient amount of inflation, it is necessary to keep the ``false'' vacuum fairly stable. In such a case, the bubble nucleation rate is small and even the resulting bubbles do not coalesce together efficiently. The final configuration is very inhomogeneous and quite different from the universe we need.
The original model was soon replaced by a version based on a very
special form for V ( ) called
the Coleman-Weinberg potential
(3,
74,
75).
At zero temperature, this potential is given by
(25)
) called
the Coleman-Weinberg potential
(3,
74,
75).
At zero temperature, this potential is given by
(25)
This potential is extremely flat for
Figure 4. The Coleman-Weinberg potential
that was used in the first major revision of the inflationary model.
where we have ignored the
For the typical values of the Co1eman-Weinberg potential, this number
can easily be about 102, thus ensuring sufficient inflation.
As
Though it is an improvement on the original version, this model,
too, is not free from problems. The field should start its slow roll
over from a value
The original model for inflation used a strongly first order phase
transition whereas the second model may be considered to be using a
weakly first order (or even second order) phase transition. It is
possible to construct inflationary scenarios in which no phase
transition is involved. The idea of chaotic inflation, suggested by
Linde, falls in this class
(76).
In this model, the potential has a
very simple form: V (
A further epicycle in the saga of inflation envisages a universe
whose origin was without a big bang
(77).
In this version, the de
Sitter type inflationary phase is self-reproducing in a chaotic set up
with the help of large scale quantum fluctuations of a scalar field
An attractive feature of the de Sitter expansion is that because of
its rapidity, the universe loses all information on initial
conditions. This is a conjecture known as the cosmic baldness
hypothesis (10).
It has not been rigorously proved but looks
plausible. On the basis of this hypothesis, one can assert that
whatever the initial conditions, the universe will eventually reach
the de Sitter state.
A solution to the bubble nucleation and coelescence problem of the
original Guth model (sometimes referred to as the graceful exit
problem) was proposed in yet another way by La & Steinhardt
(71). In
their extended inflationary cosmology, these authors used the
Brans-Dicke theory of gravity
(see 20)
instead of general relativity
as the background theory for the early universe. The inflationary
phase in this model has a power law type of expansion factor instead
of the exponential one, thus allowing the inflationary phase to end
gracefully through bubble nucleation.
Nevertheless, this idea also ran into trouble with distortions of
the MBR and was changed to hyper-extended inflation. The background
theory of gravity for this model differs from the Brans-Dicke theory
through the inclusion of higher order couplings of the scalar field
with gravity (113).
In a rapidly changing subject in which the
half-life of a theory is one year, passing judgment on the merits of
this scenario is difficult.
The schemes and shortcomings discussed above are typical of several
other models suggested in the literature. The most serious constraint
on inflationary scenarios arises from the study of density
perturbations (discussed in detail in
Section 4). No single model for
inflation suggested so far can be considered completely satisfactory.
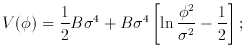


 and drops rapidly near
and drops rapidly near 

 . At finite temperatures, the
potential picks up a small barrier
near the origin [at
. At finite temperatures, the
potential picks up a small barrier
near the origin [at 
 O (T)] with height O
(T4), creating a local
minimum at
O (T)] with height O
(T4), creating a local
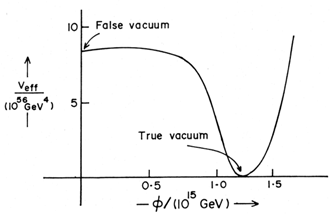
minimum at  = 0 (see
Figure 4). This false vacuum, however, is quite
unstable when the temperature becomes O (109 GeV)
(74). The scalar
field rapidly tunnels to
= 0 (see
Figure 4). This false vacuum, however, is quite
unstable when the temperature becomes O (109 GeV)
(74). The scalar
field rapidly tunnels to 

 0
0  O
(H), and starts ``rolling down'' the
gently sloped potential toward
O
(H), and starts ``rolling down'' the
gently sloped potential toward  =
=
 . Since the potential is nearly
flat in this region, the energy density driving the universe is
approximately constant and about V (0)
. Since the potential is nearly
flat in this region, the energy density driving the universe is
approximately constant and about V (0)  (3 x 1014 GeV)4. The evolution
of the scalar field in this slow rollover phase can be approximated as
(3 x 1014 GeV)4. The evolution
of the scalar field in this slow rollover phase can be approximated as
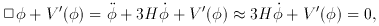
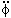 term and H = (4
term and H = (4  BG
BG  / 3c2)
/ 3c2)  2 x 1010 GeV
(in energy units). If the slow roll over lasts when
2 x 1010 GeV
(in energy units). If the slow roll over lasts when  varies from
varies from
 start
start  O (H) to some
O (H) to some  end
end  O (
O ( ), then
), then
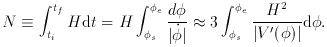
 0 approaches
0 approaches  , the field ``falls down'' the
potential and
oscillates around the minimum at
, the field ``falls down'' the
potential and
oscillates around the minimum at  =
=
 with the frequency
with the frequency  2 = V"(
2 = V"( )
)
 (2 x 1014
GeV)2 >> H2. These oscillations are damped
by the decay of
(2 x 1014
GeV)2 >> H2. These oscillations are damped
by the decay of
 into other particles (with some
decay time
into other particles (with some
decay time  -1, say);
and by the
expansion of the universe. If
-1, say);
and by the
expansion of the universe. If  -1 << H-1, the coherent-field energy
(1/2
-1 << H-1, the coherent-field energy
(1/2  2 + V)
will be converted into relativistic particles in a timescale
2 + V)
will be converted into relativistic particles in a timescale
 treheat
treheat 
 -1 << H-1. This will allow the
universe to be reheated to a
temperature of about Treheat
-1 << H-1. This will allow the
universe to be reheated to a
temperature of about Treheat 
 2 x 1014 GeV
2 x 1014 GeV  Tinitial. The decay
width of several Coleman-Weinberg models can be about
Tinitial. The decay
width of several Coleman-Weinberg models can be about  -1
-1  1013 GeV
>> H. This ensures good ``reheating'' of the universe
(2,
4,
36).
Because the field has already tunneled out of the false vacuum before
the onset of inflation, we do not face the problems that plagued the
original inflation. Instead of several bubbles having to collide,
coelesce, and make up the whole observable universe of today, we have
one huge bubble encompassing everything observable now.
1013 GeV
>> H. This ensures good ``reheating'' of the universe
(2,
4,
36).
Because the field has already tunneled out of the false vacuum before
the onset of inflation, we do not face the problems that plagued the
original inflation. Instead of several bubbles having to collide,
coelesce, and make up the whole observable universe of today, we have
one huge bubble encompassing everything observable now.
 s
s  H to ensure sufficient
inflation. The quantum
fluctuations in the scalar field are about
H to ensure sufficient
inflation. The quantum
fluctuations in the scalar field are about 

 (H / 2
(H / 2 )
(75,
120).
Since
)
(75,
120).
Since  s ~
s ~ 
 , the entire analysis based on semiclassical V (
, the entire analysis based on semiclassical V ( ) is of
doubtful validity. The second and more serious difficulty stems from
the calculation of density perturbations in this model: They are too
large by a factor of about 106, unless the parameter B
is artificially reduced by a factor 10-12 or so! (See
Section 4.)
) is of
doubtful validity. The second and more serious difficulty stems from
the calculation of density perturbations in this model: They are too
large by a factor of about 106, unless the parameter B
is artificially reduced by a factor 10-12 or so! (See
Section 4.)
 ) =
) =

 4. inflation results because of the rather
slow motion of
4. inflation results because of the rather
slow motion of  from some initial
value
from some initial
value  0 toward the
minimum. (The
initial nonzero value of the
0 toward the
minimum. (The
initial nonzero value of the  0 is supposed to be due to ``chaotic''
initial conditions.) This model can also lead to sufficient inflation
but suffers from two other difficulties: (a) To obtain the correct
value for the density perturbation, it is necessary to fine-tune
0 is supposed to be due to ``chaotic''
initial conditions.) This model can also lead to sufficient inflation
but suffers from two other difficulties: (a) To obtain the correct
value for the density perturbation, it is necessary to fine-tune  to
very small values:
to
very small values: 
 4 x 10-14. (b)
In order for the inflation to
take place, the kinetic energy of the scalar field has to be small
compared to its potential energy. Detailed calculation shows that this
requires the field to be uniform over sizes bigger than the Hubble
radius, a requirement completely against the original spirit of
inflation!
4 x 10-14. (b)
In order for the inflation to
take place, the kinetic energy of the scalar field has to be small
compared to its potential energy. Detailed calculation shows that this
requires the field to be uniform over sizes bigger than the Hubble
radius, a requirement completely against the original spirit of
inflation!
 . The bubbles of FRW models are
nucleated in it at random points of
space and time through quantum phase transitions.
. The bubbles of FRW models are
nucleated in it at random points of
space and time through quantum phase transitions.