


5.2. The Intrinsic versus Ensemble BE
Detailed comparisons of the global and intrinsic BEs have drawn
attention to the different slopes exhibited in Baldwin diagrams for
the two trends, with the intrinsic effect systematically steeper in
W versus
L (e.g., KRK).
As a quantitative example, AGN
ensembles plotted in the W
versus
L (e.g., KRK).
As a quantitative example, AGN
ensembles plotted in the W (C IV) versus continuum luminosity
plane typically display a logarithmic slope of ~ -0.1 to -0.3
(Korista et al. 1998 and references therein), while variable sources
display slopes of ~ -0.3 to -0.9
(KRK;
Edelson et al. 1990).
While this contrast may be ascribed in general terms to the
differences between static and time-variable systems, some additional
examination of this issue is potentially informative.
(C IV) versus continuum luminosity
plane typically display a logarithmic slope of ~ -0.1 to -0.3
(Korista et al. 1998 and references therein), while variable sources
display slopes of ~ -0.3 to -0.9
(KRK;
Edelson et al. 1990).
While this contrast may be ascribed in general terms to the
differences between static and time-variable systems, some additional
examination of this issue is potentially informative.
Quasars and Seyfert galaxies have quite similar spectra, to first
order, which implies that their broad-line regions scale in some
nearly uniform sense, in terms of covering factor, velocity field,
density, ionization parameter, etc. The ensemble Baldwin Effect tells
us that this scaling is not altogether homologous, although the
luminosity dependence is weak - a factor of 10 variation in
W (C IV)
over 6 orders of magnitude in L. Quasars evidently
undergo significant evolution in luminosity, and we can thus consider
the behavior of line emission as a Seyfert evolves to a quasar, or
vice versa. A variable Seyfert nucleus (e.g., Fairall 9, with a
factor of 30 variation in luminosity; see
Figure 5) arguably
represents this process in miniature. That being the case, it is
perhaps surprising that the intrinsic and global BEs are so different,
i.e., Seyfert nuclei do not simply slide along the locus of the
ensemble relation as they vary.
(C IV)
over 6 orders of magnitude in L. Quasars evidently
undergo significant evolution in luminosity, and we can thus consider
the behavior of line emission as a Seyfert evolves to a quasar, or
vice versa. A variable Seyfert nucleus (e.g., Fairall 9, with a
factor of 30 variation in luminosity; see
Figure 5) arguably
represents this process in miniature. That being the case, it is
perhaps surprising that the intrinsic and global BEs are so different,
i.e., Seyfert nuclei do not simply slide along the locus of the
ensemble relation as they vary.
Some perspective on the intrinsic versus ensemble behavior can be
derived from considering quasar luminosity evolution in conjunction
with the locally optimally-emitting cloud (LOC) model for the BLR
(Baldwin et al. 1995).
The essential idea of the LOC
model is that clouds emit with high efficiency in a given line only in
a rather restricted portion of the parameter space of cloud density n
and incident ionizing flux  (or
distance r from the continuum
source) (5).
If we consider an ensemble of clouds surrounding a continuum source,
we can imagine correspondingly a zone in radius where clouds with the
appropriate density will dominate the total emission in, say, C IV;
clouds at smaller radii are either too dense or too highly
ionized to emit strongly in this line, while clouds at larger radii
will have little C+3 or lie outside the BLR. If we were to
increase the luminosity of the central continuum source, the radius
describing the region of efficient C IV emission would move
outward. The effect on W
(or
distance r from the continuum
source) (5).
If we consider an ensemble of clouds surrounding a continuum source,
we can imagine correspondingly a zone in radius where clouds with the
appropriate density will dominate the total emission in, say, C IV;
clouds at smaller radii are either too dense or too highly
ionized to emit strongly in this line, while clouds at larger radii
will have little C+3 or lie outside the BLR. If we were to
increase the luminosity of the central continuum source, the radius
describing the region of efficient C IV emission would move
outward. The effect on W (C IV) would then depend on
cloud covering factor as a function of radius (see
Figure 7).
(C IV) would then depend on
cloud covering factor as a function of radius (see
Figure 7).
If the covering factor fc of the clouds diminishes
rapidly with
radius, we would expect the line equivalent width to decrease as the
source brightens (a Baldwin Effect); correspondingly, radial
distributions should also exist that would yield an increase in
equivalent width for higher L (an anti-Baldwin Effect). What radial
distribution constitutes the intermediate case, corresponding to the
homologous BLR? To obtain W independent of L, the
fractional coverage
independent of L, the
fractional coverage  fc represented by clouds with a given
density, within an interval of incident flux
fc represented by clouds with a given
density, within an interval of incident flux 
 , should be
independent of L. The relevant differential covering factor is then
, should be
independent of L. The relevant differential covering factor is then
Note that r
which is homologous and independent of L if
If the intrinsic Baldwin Effect ultimately stems from a steep fall-off
in circumnuclear covering factor (
An important independent constraint on fc(r) is
available from global fits to quasar spectra.
Baldwin (1997)
has reviewed the LOC
model and its predictions for relative line strengths as a function of
fc(r), parametrized in terms of the differential
power-law index
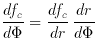
 sqrt(L /
sqrt(L /  ), so that dr / d
), so that dr / d 
 L1/2
L1/2  -3/2. If we express dfc / dr
-3/2. If we express dfc / dr  r
r , then
dfc / dr
, then
dfc / dr  L
L /2
/2  -
- /2,
and
/2,
and
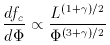
 = -1.
= -1.
 < -1), then the luminosity
evolution of AGNs must be accompanied (perhaps unsurprisingly) by
substantial structural changes within the BLR, in terms of the distribution
of matter. A less violent adjustment is required for a homologous profile,
which in turn provides a natural basis for producing grossly similar
Seyfert and quasar spectra. The structure of fc(r)
thus contains
potentially significant information on the physical evolution of AGNs.
< -1), then the luminosity
evolution of AGNs must be accompanied (perhaps unsurprisingly) by
substantial structural changes within the BLR, in terms of the distribution
of matter. A less violent adjustment is required for a homologous profile,
which in turn provides a natural basis for producing grossly similar
Seyfert and quasar spectra. The structure of fc(r)
thus contains
potentially significant information on the physical evolution of AGNs.
 . As can be seen
from his Figure 1, good agreement with the
average quasar spectrum is obtained with
. As can be seen
from his Figure 1, good agreement with the
average quasar spectrum is obtained with  = -1, which may
imply that the BLR is indeed homologous. In this case the dominant
cause underlying the intrinsic BE is likely to be variability and
light travel-time effects, as discussed in the previous section.
Further comparisons of this type, perhaps including added constraints from
linewidth measurements, may provide stronger constraints on
= -1, which may
imply that the BLR is indeed homologous. In this case the dominant
cause underlying the intrinsic BE is likely to be variability and
light travel-time effects, as discussed in the previous section.
Further comparisons of this type, perhaps including added constraints from
linewidth measurements, may provide stronger constraints on  and hence BLR structure, as well as the origins of the intrinsic BE.
and hence BLR structure, as well as the origins of the intrinsic BE.
5 Column density represents another free parameter
describing the clouds, and the distribution of column densities will
influence the proportions of ionization- and matter-bounded clouds.
Back.