

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
3.2 Dynamics of the Expansion
EXPANSION AND GEOMETRY
Note that this equation covers all contributions
to
The Friedmann equation shows that a universe that is spatially closed
(with k = +1) has negative
total ``energy'': the expansion will eventually be halted
by gravity, and the universe will recollapse.
Conversely, an unbound model is spatially open
(k = -1) and will expand forever.
This is marvelously simple: the dynamics of the entire
universe are the same as those of a cannonball fired
vertically against the Earth's gravity.
Just as the Earth's gravity defines an escape velocity for projectiles,
so a universe that expands sufficiently fast will
continue to expand forever.
Conversely, for a given rate of expansion there is a
critical density that will bring the
expansion asymptotically to a halt:
This connection between the rate of expansion of the
universe and its global geometry is an astonishing
and deep result. The proof of the equation quoted
above is ``only'' a question of inserting the Robertson-Walker
metric into the field equations [problem 3.1], but the
question inevitably arises of whether there is a
quasi-Newtonian way of seeing that the result must be true;
the answer is ``almost''.
First note that any open model will evolve towards
undecelerated expansion provided its equation of
state is such that
An alternative line of attack is to rewrite the Friedmann
equation in terms of the Hubble parameter:
Now consider holding the local observables H and
It is sometimes convenient to work with the time derivative
of the Friedmann equation, for the same reason that
acceleration arguments in dynamics are sometimes
more transparent than energy ones. Differentiating
with respect to time requires a knowledge of
Both this equation and the Friedmann equation in fact
arise as independent equations from different components
of Einstein's equations for the RW metric [problem 3.1].
DENSITY PARAMETERS ETC.
Since
then the current density of the universe may be expressed as
A powerful approximate model for the energy content of the
universe is to divide it into pressureless matter
(
(introducing the normalized scale factor a = R / R0).
For some purposes, this separation is unnecessary, since the
Friedmann equation treats all contributions to the density parameter equally:
Thus, a flat k = 0 universe requires
In terms of the deceleration parameter,
the
which implies q = 3
Lastly, it is often necessary to know the present
value of the scale factor, which may be read directly from the
Friedmann equation:
The Hubble constant thus sets the curvature length,
which becomes infinitely large as
SOLUTIONS TO THE FRIEDMANN EQUATION
The Friedmann equation may be solved most simply in
``parametric'' form, by recasting it in terms of the
conformal time d
Because H02
R02 = kc2 / (
which is straightforward to integrate provided
To the observer, the evolution of the scale factor is
most directly characterised by the change with redshift
of the Hubble parameter and the density parameter;
the evolution of H (z) and
This is a crucial equation, which can be used to obtain
the relation between
redshift and comoving distance. The radial equation of motion
for a photon is R dr = c dt = c dR /
This relation is arguably the single most important equation in
cosmology, since it shows how to relate comoving distance
to the observables of redshift, Hubble constant and density
parameters. The comoving distance determines the apparent
brightness of distant objects, and the comoving volume
element determines the numbers of objects that are observed.
These aspect of observational cosmology are discussed in
more detail below in section 3.4.
Lastly, using the expression for H (z) with
This last equation is very important. It tells us that, at
high redshift, all model universes apart from those
with only vacuum energy will tend to look like
the
MATTER-DOMINATED UNIVERSE
At redshifts higher than this, the universal dynamics were
dominated by the relativistic-particle content.
By a coincidence discussed below, this epoch is close
to another important event in cosmological history:
recombination. Once the temperature falls below
By conserving matter,
we can introduce a characteristic mass M*,
and from this a characteristic radius R*:
where we have used the expression for R0 in the first step.
When only matter is present, the conformal-time version of the
Friedmann equation is simple to integrate for R (
This cycloid solution
is a special case of the general solution for the evolution of
a spherical mass distribution:
R = A [1 - Ck (
At this point, we have reproduced one of the great
conclusions of relativistic cosmology: the universe is of
finite age, and had its origin in a mathematical
singularity at which the scale factor went to zero,
leading to a divergent spacetime curvature.
Since zero scale factor also implies infinite density (and
temperature), the inferred picture of the early universe is one
of unimaginable violence. The term big bang was
coined by Fred Hoyle to describe this beginning, although it was intended
somewhat critically. The problem with the singularity is
that it marks the breakdown of the laws of physics;
we cannot extrapolate the solution for R (t) to t < 0, and
so the origin of the expansion becomes an unexplained
boundary condition. It was only after about 1980 that a
consistent set of ideas became available
for ways of avoiding this barrier, as discussed in chapter 11.
The parametric solution cannot be rearranged to give
R (t), but it is clearly possible to solve for t (R).
This is most simply expressed
in terms of the density parameter and the age of the universe
at a given stage of its development:
When we insert the redshift dependences of H (z) and
this gives us the time-redshift relation.
An alternative route to this result would have been
to use the general differential expression for comoving distance dr /
dz; since c dt = [R0 / (1 + z)]
dr, this gives the age of the universe as an integral over z.
An accurate and very useful approximation to the above exact result is
which interpolates between the exact ages of H-1 for
an empty universe and 2/3 H-1 for a critical-density
MATTER PLUS RADIATION BACKGROUND
reflecting the R-3 and R-4
dependencies of matter and radiation densities respectively. Now define
dimensionless masses of the form y
MODELS WITH VACUUM ENERGY
The Friedmann equation itself is independent of the
equation of state, and just says H2
R2 = kc2 / (
STATIC UNIVERSE
Since
Since
Notice that what this says is that a positive
vacuum energy acts in a repulsive way, balancing
the attraction of normal matter. This is related
to the idea of
DE SITTER SPACE
An interesting interpretation of this behaviour
was promoted in the early days of cosmology by Eddington:
the cosmological constant is what caused the
expansion. In models without
THE STEADY-STATE MODEL
The effect of this extra term must be to cancel
the matter density and pressure, leaving just the overall
effective form of the vacuum tensor, which is required to
produce de Sitter space and the exponential expansion.
This ad hoc field and the lack of any physical motivation for
it beyond the cosmological problem it was designed to solve
was always the most unsatisfactory feature of the steady-state
model, and may account for the strong reactions generated by the theory.
Certainly, the debate between steady-state supporters and protagonists
of the big bang produced some memorable displays of vitriol in the
1960s. At the start of the decade, the point at issue was whether the
proper density of active galaxies was constant as predicted by the
steady-state model. Since the radio-source count data were in a somewhat
primitive state at that time, the debate remained inconclusive until the
detection of the microwave background in 1965. For many, this spelled
the end of the steady-state universe, but doubts lingered on about
whether the radiation might originate in interstellar dust.
These were perhaps only finally laid to rest in 1990,
with the demonstration that the radiation was
almost exactly Planckian in form (see chapter 9).
BOUNCING AND LOITERING MODELS
and we are interested in the conditions under which
the lhs vanishes, defining a turning point in the expansion.
Setting the rhs to zero yields a cubic equation, and it
is possible to give the conditions under which this has a
solution (see Felten & Isaacman 1986), which are as
follows.
If
If
If
where the function f is similar in spirit to Ck:
cosh if
In fact, bounce models can be ruled out quite strongly.
The same cubic equations that define the critical
conditions for a bounce also give an inequality for
the maximum redshift possible (that of the bounce):
A reasonable lower limit for
The main results of this section are summed up in
figure 3.5..
Since the radiation density is very small today,
the main task of relativistic cosmology is to work out
where on the
FLAT UNIVERSE
Although it is a
mathematically distinct case, in practice
the properties of a flat model can usually
be obtained by taking the limit
It now makes more sense to work throughout in terms of the normalized
scale factor a (t), so that the Friedmann equation for a
matter-radiation mix is
which may be integrated to give the time as a function of scale factor:
this goes to 2/3 a3/2 for a matter-only model,
and to 1/2 a2 for radiation only.
One further way of presenting the model's dependence on time
is via the density. Following the above, it is easy to show that
The whole universe thus always obeys the rule-of-thumb for the
collapse from rest of a gravitating body:
the collapse time
Because
and the t (a) relation is
The x4 on the bottom looks like trouble, but it can be
rendered tractable by the substitution y =
sqrt(x3 |
Here, k in Sk is used to mean sin if
where we include a simple approximation that is accurate to a few % over the
region of interest (
HORIZONS
i.e. just the interval of conformal time.
What happens as t0 -> 0 in this expression? We can
replace dt by dR /
A particle horizon is not at all the same thing as an event horizon:
for the latter, we ask whether
There are some unique aspects to
the idea of a horizon in a closed universe, where
you can in principle return to your starting point by
continuing for long enough in the same direction. However, the
related possibility of viewing the back of your head (albeit
with some time delay) turns out to be more difficult once dynamics
are taken into account. For a matter-only model,
it is easy to show that the horizon
only just reaches the stage of allowing a photon to circumnavigate
the universe at the point of recollapse - the ``big crunch''.
A photon that starts at r = 0 at t = 0 will return to its initial
position when r = 2 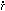 r)2 / 2 - GM
/ (Rr) = constant. In fact, to get this far, we do require general
relativity: the gravitation from mass shells at large distances is not
Newtonian, and so we cannot employ the usual argument about
their effect being zero. In fact, the result that the
gravitational field inside a uniform shell is zero
does hold in general relativity, and is known as Birkhoff's
theorem (see chapter 2).
General relativity becomes even more vital in giving us the constant
of integration in Friedmann's equation [problem 3.1]:
r)2 / 2 - GM
/ (Rr) = constant. In fact, to get this far, we do require general
relativity: the gravitation from mass shells at large distances is not
Newtonian, and so we cannot employ the usual argument about
their effect being zero. In fact, the result that the
gravitational field inside a uniform shell is zero
does hold in general relativity, and is known as Birkhoff's
theorem (see chapter 2).
General relativity becomes even more vital in giving us the constant
of integration in Friedmann's equation [problem 3.1]:
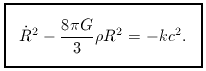
 , i.e. those from
matter, radiation and vacuum; it is independent
of the equation of state.
A common shorthand for relativistic cosmological models,
which are described by the Robertson-Walker metric and
which obey the Friedmann equation, is to speak of FRW models.
, i.e. those from
matter, radiation and vacuum; it is independent
of the equation of state.
A common shorthand for relativistic cosmological models,
which are described by the Robertson-Walker metric and
which obey the Friedmann equation, is to speak of FRW models.
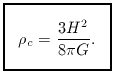
 R2 is a declining function of R -
the potential energy becomes negligible by comparison with the total
and
R2 is a declining function of R -
the potential energy becomes negligible by comparison with the total
and  tends to a constant. In this
mass-free limit, there
can be no spatial curvature and the open RW metric must
be just a coordinate transformation of Minkowski spacetime.
We will exhibit transformation later in this chapter
and show that it implies
R = ct for this model, proving the k = -1 case.
tends to a constant. In this
mass-free limit, there
can be no spatial curvature and the open RW metric must
be just a coordinate transformation of Minkowski spacetime.
We will exhibit transformation later in this chapter
and show that it implies
R = ct for this model, proving the k = -1 case.
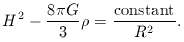
 fixed but increasing
R without limit. Clearly, in
the RW metric this corresponds to going to the k = 0 form:
the scale of spatial curvature goes to infinity and
the comoving separation for any given proper separation
goes to zero, so that the comoving
geometry becomes indistinguishable from the Euclidean form.
This case also has potential
and kinetic energy much greater than total energy, so that the
rhs of the Friedmann equation is effectively zero.
This establishes the k = 0 case, leaving the closed
universe as the only stubborn holdout against Newtonian arguments.
fixed but increasing
R without limit. Clearly, in
the RW metric this corresponds to going to the k = 0 form:
the scale of spatial curvature goes to infinity and
the comoving separation for any given proper separation
goes to zero, so that the comoving
geometry becomes indistinguishable from the Euclidean form.
This case also has potential
and kinetic energy much greater than total energy, so that the
rhs of the Friedmann equation is effectively zero.
This establishes the k = 0 case, leaving the closed
universe as the only stubborn holdout against Newtonian arguments.
 ,
but this can be eliminated by means of conservation of energy:
d [
,
but this can be eliminated by means of conservation of energy:
d [ c2 R3] = -pd
[R3]. We then obtain
c2 R3] = -pd
[R3]. We then obtain
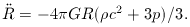
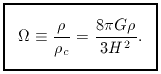
 and H
change with time, this defines an epoch-dependent density parameter. The
current value of the parameter should
strictly be denoted by
and H
change with time, this defines an epoch-dependent density parameter. The
current value of the parameter should
strictly be denoted by  0. Because this is
such a common symbol, we shall keep the formulae
uncluttered by normally dropping the subscript;
the density parameter at
other epochs will be denoted by
0. Because this is
such a common symbol, we shall keep the formulae
uncluttered by normally dropping the subscript;
the density parameter at
other epochs will be denoted by  (z).
The critical density therefore just depends on the
rate at which the universe is expanding.
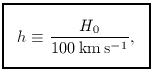
If we now also define a dimensionless (current) Hubble parameter as
(z).
The critical density therefore just depends on the
rate at which the universe is expanding.
If we now also define a dimensionless (current) Hubble parameter as
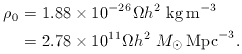

 R-3),
radiation (
R-3),
radiation (
 R-4) and vacuum energy
(
R-4) and vacuum energy
( constant).
The first two relations just say that the number density
of particles is diluted by the expansion, with photons also
having their energy reduced by the redshift; the third relation
applies for Einstein's cosmological constant.
In terms of observables, this means that the density is written as
constant).
The first two relations just say that the number density
of particles is diluted by the expansion, with photons also
having their energy reduced by the redshift; the third relation
applies for Einstein's cosmological constant.
In terms of observables, this means that the density is written as
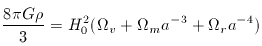
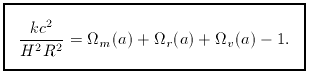

 i = 1 at all times,
whatever the form of the contributions to the density, even if the
equation of state cannot be decomposed in this simple way.
i = 1 at all times,
whatever the form of the contributions to the density, even if the
equation of state cannot be decomposed in this simple way.
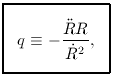
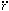 form of the Friedmann
equation says that
form of the Friedmann
equation says that
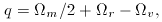
 m / 2 + 2
m / 2 + 2 r -1 for a flat universe.
One of the classical problems of cosmology is to
test this relation experimentally.
r -1 for a flat universe.
One of the classical problems of cosmology is to
test this relation experimentally.
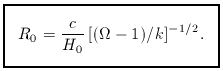
 approaches unity from
either direction. Only in the limit of zero density
does this length become equal to the other common measure
of the size of the universe - the Hubble length, c /
H0.
approaches unity from
either direction. Only in the limit of zero density
does this length become equal to the other common measure
of the size of the universe - the Hubble length, c /
H0.
 = c dt / R (denoting derivatives
with respect to
= c dt / R (denoting derivatives
with respect to  by
primes):
by
primes):
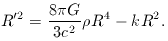
 - 1), the Friedmann equation becomes
- 1), the Friedmann equation becomes
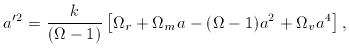
 v = 0.
Solving the Friedmann equation for R (t) in this way is
important for determining global quantities such as the
present age of the universe, and explicit solutions for
particular cases are considered below.
However, from the point of view of observations, and in
particular the distance-redshift relation, it is
not necessary to proceed by the direct route of
determining R (t).
v = 0.
Solving the Friedmann equation for R (t) in this way is
important for determining global quantities such as the
present age of the universe, and explicit solutions for
particular cases are considered below.
However, from the point of view of observations, and in
particular the distance-redshift relation, it is
not necessary to proceed by the direct route of
determining R (t).
 (z) is given immediately
by the Friedmann equation in the form
H2 = 8
(z) is given immediately
by the Friedmann equation in the form
H2 = 8  G
G
 / 3 -
kc2 / R2. Inserting the above dependence of
/ 3 -
kc2 / R2. Inserting the above dependence of
 on a gives
on a gives
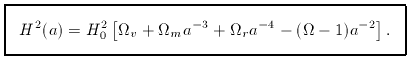
 = c dR / (RH).
With R = R0 / (1 + z), this gives
= c dR / (RH).
With R = R0 / (1 + z), this gives
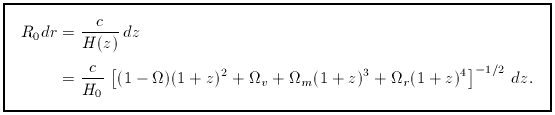
 (a) - 1 =
kc2 / (H2 R2) gives
the redshift dependence of the total density parameter:
(a) - 1 =
kc2 / (H2 R2) gives
the redshift dependence of the total density parameter:
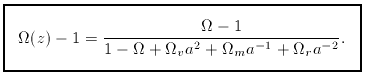
 = 1 model. This is not
surprising given the
form of the Friedmann equation: provided
= 1 model. This is not
surprising given the
form of the Friedmann equation: provided  R2 ->
R2 ->  as R -> 0, the -kc2 curvature term will become
negligible at early times.
If
as R -> 0, the -kc2 curvature term will become
negligible at early times.
If 
 1, then in the distant
past
1, then in the distant
past  (z) must
have differed from unity by a tiny amount: the density and
rate of expansion needed to have been finely balanced for the
universe to expand to the present. This tuning of the initial
conditions is called the flatness problem and is one of
the motivations for the applications of quantum theory to
the early universe that are discussed in later chapters.
(z) must
have differed from unity by a tiny amount: the density and
rate of expansion needed to have been finely balanced for the
universe to expand to the present. This tuning of the initial
conditions is called the flatness problem and is one of
the motivations for the applications of quantum theory to
the early universe that are discussed in later chapters.
 r h2
r h2  4.2 x 10-5, so at present
it should be a good approximation to ignore radiation.
However, the different redshift dependences of matter and
radiation densities mean that this assumption fails at
early times:
4.2 x 10-5, so at present
it should be a good approximation to ignore radiation.
However, the different redshift dependences of matter and
radiation densities mean that this assumption fails at
early times:  m /
m /  r
r  (1
+ z)-1.
One of the critical epochs in cosmology is therefore
the point at which these contributions were equal:
the redshift of matter-radiation equality
(1
+ z)-1.
One of the critical epochs in cosmology is therefore
the point at which these contributions were equal:
the redshift of matter-radiation equality
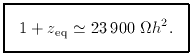
 104 K,
ionized material can form neutral hydrogen. Observational
astronomy is only possible from this point on, since
Thomson scattering from electrons in ionized
material prevents photon propagation. In practice, this
limits the maximum redshift of observational interest to
about 1000 (as discussed in detail in chapter 9); unless
104 K,
ionized material can form neutral hydrogen. Observational
astronomy is only possible from this point on, since
Thomson scattering from electrons in ionized
material prevents photon propagation. In practice, this
limits the maximum redshift of observational interest to
about 1000 (as discussed in detail in chapter 9); unless
 is very low or vacuum energy
is important, a matter-dominated model is therefore a good approximation
to reality.
is very low or vacuum energy
is important, a matter-dominated model is therefore a good approximation
to reality.
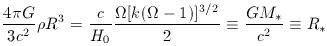
 ), and
integration of dt = d
), and
integration of dt = d / R gives t (
/ R gives t ( ):
):
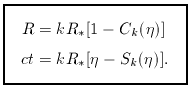
 )],
t = B [
)],
t = B [ - Sk (
- Sk ( )], where A3 = GMB2 and
the mass M need not be the mass of the universe.
In the general case, the variable
)], where A3 = GMB2 and
the mass M need not be the mass of the universe.
In the general case, the variable  is known as the
development angle; it is only equal to the conformal
time in the special case of the solution to the Friedmann equation.
We will later use this solution to
study the evolution of density inhomogeneities.
The evolution of R (t) in this solution is plotted in
figure 3.4. A particular
point to note is that the behaviour at early times is
always the same: potential and kinetic
energies greatly exceed total energy and we always have the
k = 0 form R
is known as the
development angle; it is only equal to the conformal
time in the special case of the solution to the Friedmann equation.
We will later use this solution to
study the evolution of density inhomogeneities.
The evolution of R (t) in this solution is plotted in
figure 3.4. A particular
point to note is that the behaviour at early times is
always the same: potential and kinetic
energies greatly exceed total energy and we always have the
k = 0 form R  t2/3.
t2/3.
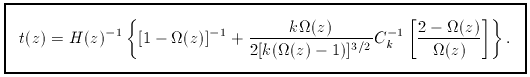
 (z),
(z),
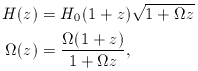
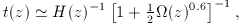
 = 1 model.
= 1 model.
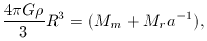
 GM / (c2 R0), which
reduce to ym, r = k
GM / (c2 R0), which
reduce to ym, r = k  m, r / [2(
m, r / [2( - 1)].
The parametric solutions then become
- 1)].
The parametric solutions then become
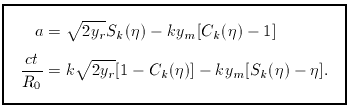
 - 1),
whatever the form of the contributions to
- 1),
whatever the form of the contributions to  . In terms of the cosmological constant itself, we have
. In terms of the cosmological constant itself, we have
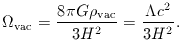
 =
=  ; if we
cast the equation in its original form without defining
these parameters, then zero expansion implies
; if we
cast the equation in its original form without defining
these parameters, then zero expansion implies
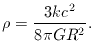
 can have either sign,
this appears not to constrain k. However, we also want to have
zero acceleration for this model, and so need the
time derivative of the Friedmann equation:
can have either sign,
this appears not to constrain k. However, we also want to have
zero acceleration for this model, and so need the
time derivative of the Friedmann equation:
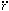 = -4
= -4  GR
(
GR
( + 3p) / 3. A
further condition for a static model is therefore that
+ 3p) / 3. A
further condition for a static model is therefore that
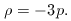
 = -p
for vacuum energy, and this is the only
source of pressure if we ignore radiation, this tells
us that
= -p
for vacuum energy, and this is the only
source of pressure if we ignore radiation, this tells
us that  = 3
= 3 vac and hence that the
mass density is twice the vacuum density. The total
density is hence positive and k = 1; we have a closed model.
vac and hence that the
mass density is twice the vacuum density. The total
density is hence positive and k = 1; we have a closed model.
 +
3p as the effective source density for gravity. This insight
alone should make one appreciate that the static model cannot
be stable: if we perturb the scale factor by a small positive amount,
the vacuum repulsion is unchanged whereas the ``normal'' gravitational
attraction is reduced, so that the model will tend to expand further (or
contract, if the initial perturbation was negative). Thinking along these
lines, a tidy history of science would have required Einstein to predict
the expanding universe in advance of its observation. However, it is
perhaps not so surprising that this prediction was never clearly made,
despite the fact that expanding models were studied by Lemaître
and by Friedmann in the years prior to Hubble's
work. In those days, the idea of a quasi-Newtonian
approach to cosmology was not developed; the common
difficulty of obtaining a clear physical interpretation
of solutions to Einstein's equations obscured the
meaning of the expanding universe even for its creators.
+
3p as the effective source density for gravity. This insight
alone should make one appreciate that the static model cannot
be stable: if we perturb the scale factor by a small positive amount,
the vacuum repulsion is unchanged whereas the ``normal'' gravitational
attraction is reduced, so that the model will tend to expand further (or
contract, if the initial perturbation was negative). Thinking along these
lines, a tidy history of science would have required Einstein to predict
the expanding universe in advance of its observation. However, it is
perhaps not so surprising that this prediction was never clearly made,
despite the fact that expanding models were studied by Lemaître
and by Friedmann in the years prior to Hubble's
work. In those days, the idea of a quasi-Newtonian
approach to cosmology was not developed; the common
difficulty of obtaining a clear physical interpretation
of solutions to Einstein's equations obscured the
meaning of the expanding universe even for its creators.
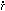 2 - 8
2 - 8  G
G
 R2
/ 3 = -kc2:
since the density is constant and R will increase without
limit, the two terms on the lhs must eventually become
almost exactly equal and the curvature term on the rhs will
be negligible. Thus, even if k
R2
/ 3 = -kc2:
since the density is constant and R will increase without
limit, the two terms on the lhs must eventually become
almost exactly equal and the curvature term on the rhs will
be negligible. Thus, even if k  0, the universe will have a density that differs only
infinitesimally from the critical, so that we can solve the equation by
setting k = 0, in which case
0, the universe will have a density that differs only
infinitesimally from the critical, so that we can solve the equation by
setting k = 0, in which case
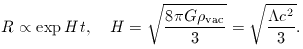
 , the expansion is merely
an initial condition: anyone who asks why the universe
expands at a given epoch is given the unsatisfactory
reply that it does so because it was expanding at
some earlier time, and this chain of reasoning
comes up against a barrier at t = 0. It would be more satisfying to
have some mechanism that set the expansion into
motion, and this is what is provided by vacuum repulsion.
This tendency of models with positive
, the expansion is merely
an initial condition: anyone who asks why the universe
expands at a given epoch is given the unsatisfactory
reply that it does so because it was expanding at
some earlier time, and this chain of reasoning
comes up against a barrier at t = 0. It would be more satisfying to
have some mechanism that set the expansion into
motion, and this is what is provided by vacuum repulsion.
This tendency of models with positive  to end up undergoing an exponential phase of expansion
(and moreover one with
to end up undergoing an exponential phase of expansion
(and moreover one with  = 1) is
exactly what is used in inflationary cosmology to
generate the initial conditions for the big bang.
= 1) is
exactly what is used in inflationary cosmology to
generate the initial conditions for the big bang.
 exp(Ht), exactly as for de Sitter space. Furthermore, it is necessary
that k = 0, as may be seen by considering the
transverse part of the Robertson-Walker metric:
d
exp(Ht), exactly as for de Sitter space. Furthermore, it is necessary
that k = 0, as may be seen by considering the
transverse part of the Robertson-Walker metric:
d  2 = [R
(t) Sk (r) d
2 = [R
(t) Sk (r) d  ]2. This has
the convention that r is a dimensionless
comoving coordinate; if we divide by R0
and change to physical radius r', the metric becomes
d
]2. This has
the convention that r is a dimensionless
comoving coordinate; if we divide by R0
and change to physical radius r', the metric becomes
d  2 = [a
(t) R0 Sk (r' / R0)
d
2 = [a
(t) R0 Sk (r' / R0)
d  ]2.
The current scale factor R0 now plays the role
of a curvature length, determining the distance over which the model is
spatially Euclidean. However, any such curvature radius must be constant
in the steady-state model, so the only possibility is that it is infinite
and that k = 0. We thus see that de Sitter space is a steady-state
universe: it contains a constant vacuum energy density, and has an
infinite age, lacking any big-bang singularity. In this sense, some
aspects of the steady-state model have been resurrected in inflationary
cosmology. However, de Sitter space is a rather uninteresting
model because it contains no matter. Introducing matter into a
steady-state universe violates energy conservation, since matter does
not have the p = -
]2.
The current scale factor R0 now plays the role
of a curvature length, determining the distance over which the model is
spatially Euclidean. However, any such curvature radius must be constant
in the steady-state model, so the only possibility is that it is infinite
and that k = 0. We thus see that de Sitter space is a steady-state
universe: it contains a constant vacuum energy density, and has an
infinite age, lacking any big-bang singularity. In this sense, some
aspects of the steady-state model have been resurrected in inflationary
cosmology. However, de Sitter space is a rather uninteresting
model because it contains no matter. Introducing matter into a
steady-state universe violates energy conservation, since matter does
not have the p = - c2 equation of state that allows the
density to remain constant. This is the most radical
aspect of steady-state models: they require
continuous creation of matter. The energy to
accomplish this has to come from somewhere, and
Einstein's equations are modified by
adding some ``creation'' or ``C-field'' term to the energy-momentum
tensor:
c2 equation of state that allows the
density to remain constant. This is the most radical
aspect of steady-state models: they require
continuous creation of matter. The energy to
accomplish this has to come from somewhere, and
Einstein's equations are modified by
adding some ``creation'' or ``C-field'' term to the energy-momentum
tensor:
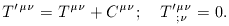
 term
and underwent a ``bounce'' to reach its present state
of expansion. Working out the conditions for these different events is a
matter of integrating the Friedmann equation.
For the addition of
term
and underwent a ``bounce'' to reach its present state
of expansion. Working out the conditions for these different events is a
matter of integrating the Friedmann equation.
For the addition of  , this can only
in general be done numerically. However, we can
find the conditions for the different behaviours
described above analytically, at least if we simplify
things by ignoring radiation. The equation in the
form of the time-dependent Hubble parameter looks like
, this can only
in general be done numerically. However, we can
find the conditions for the different behaviours
described above analytically, at least if we simplify
things by ignoring radiation. The equation in the
form of the time-dependent Hubble parameter looks like
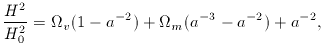
always
implies recollapse, which is intuitively reasonable (either the mass causes
recollapse before
 dominates,
or the density is low enough that
dominates,
or the density is low enough that  comes to dominate, which cannot lead to infinite expansion
unless
comes to dominate, which cannot lead to infinite expansion
unless  is positive.
is positive.
(2)
 is positive and
is positive and  m < 1, the model always
expands to infinity.
m < 1, the model always
expands to infinity.
(3)
 m > 1, recollapse
is only avoided if
m > 1, recollapse
is only avoided if  v
exceeds a critical value
v
exceeds a critical value
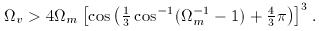
(4)
 is large enough, the
stationary point of the expansion is at a < 1 and we have a
bounce cosmology. This critical value is
is large enough, the
stationary point of the expansion is at a < 1 and we have a
bounce cosmology. This critical value is
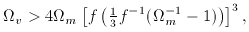
 m < 0.5,
otherwise cos. If the universe lies exactly on the critical line,
the bounce is at infinitely early times and we have a solution that is
the result of a perturbation of the Einstein static model. Models that almost
satisfy the critical
m < 0.5,
otherwise cos. If the universe lies exactly on the critical line,
the bounce is at infinitely early times and we have a solution that is
the result of a perturbation of the Einstein static model. Models that almost
satisfy the critical  v (
v ( m) relation
are known as loitering models, since they
spend a long time close to constant scale factor.
Such models were briefly popular in the early 1970s,
when there seemed to be a sharp peak in the quasar
redshift distribution at z
m) relation
are known as loitering models, since they
spend a long time close to constant scale factor.
Such models were briefly popular in the early 1970s,
when there seemed to be a sharp peak in the quasar
redshift distribution at z  2. However, this no longer seems a reasonable explanation for what
is undoubtedly a mixture of evolution and observational selection.
2. However, this no longer seems a reasonable explanation for what
is undoubtedly a mixture of evolution and observational selection.
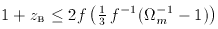
 m of 0.1 then
rules out a bounce once objects are seen at z > 2.
m of 0.1 then
rules out a bounce once objects are seen at z > 2.
 matter
-
matter
-  vacuum plane
the real universe lies. The existence of high-redshift
objects rules out the bounce models, so that the idea
of a hot big bang cannot be evaded. As subsequent
chapters will show, the data favour a position somewhere
near the point (1,0), which is the worst possible
situation: it means that the issues of recollapse
and closure are very difficult to resolve.
vacuum plane
the real universe lies. The existence of high-redshift
objects rules out the bounce models, so that the idea
of a hot big bang cannot be evaded. As subsequent
chapters will show, the data favour a position somewhere
near the point (1,0), which is the worst possible
situation: it means that the issues of recollapse
and closure are very difficult to resolve.
 total = 1; when dominated by matter,
this is often termed the Einstein-de Sitter model.
Paradoxically, this importance arises because it is
an unstable state: as we have seen earlier, the universe
will evolve away from
total = 1; when dominated by matter,
this is often termed the Einstein-de Sitter model.
Paradoxically, this importance arises because it is
an unstable state: as we have seen earlier, the universe
will evolve away from  = 1,
given a slight perturbation.
For the universe to have expanded by so many e-foldings
(factors of e expansion)
and yet still have
= 1,
given a slight perturbation.
For the universe to have expanded by so many e-foldings
(factors of e expansion)
and yet still have  ~ 1 implies
that it was very close to being spatially flat at early times. Many
workers have conjectured that it would be contrived if this flatness
was other than perfect - a prejudice raised to the status
of a prediction in most models of inflation.
~ 1 implies
that it was very close to being spatially flat at early times. Many
workers have conjectured that it would be contrived if this flatness
was other than perfect - a prejudice raised to the status
of a prediction in most models of inflation.
 -> 1
for either open or closed universes with k = ± 1.
Nevertheless, it is usually easier to start again from the
k = 0 Friedmann equation,
-> 1
for either open or closed universes with k = ± 1.
Nevertheless, it is usually easier to start again from the
k = 0 Friedmann equation, 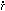 2 = 8
2 = 8  G
img src="../GIFS/rho2.gif" alt="rho" align=middle> R2
/ (3c2). Since both sides are quadratic in R,
this makes it clear that the value of R0 is arbitrary,
unlike models with
G
img src="../GIFS/rho2.gif" alt="rho" align=middle> R2
/ (3c2). Since both sides are quadratic in R,
this makes it clear that the value of R0 is arbitrary,
unlike models with 
 1:
the comoving geometry is Euclidean, and there is no natural curvature scale.
1:
the comoving geometry is Euclidean, and there is no natural curvature scale.
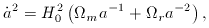
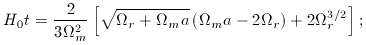
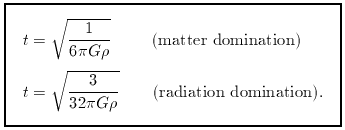
 1 /
sqrt(G
1 /
sqrt(G  ).
).
 r is so
small, the deviations from a matter-only model are unimportant for
z
r is so
small, the deviations from a matter-only model are unimportant for
z  1000, and
so the distance-redshift relation for the
k = 0 matter plus radiation model is effectively
just that of the
1000, and
so the distance-redshift relation for the
k = 0 matter plus radiation model is effectively
just that of the  m =
1 Einstein-de Sitter model.
An alternative k = 0 model of greater observational interest has a
significant cosmological constant, so that
m =
1 Einstein-de Sitter model.
An alternative k = 0 model of greater observational interest has a
significant cosmological constant, so that  m +
m +  v = 1
(radiation being neglected for simplicity).
This may seem contrived, but once k = 0 has been established,
it cannot change: individual contributions to
v = 1
(radiation being neglected for simplicity).
This may seem contrived, but once k = 0 has been established,
it cannot change: individual contributions to  must adjust to keep in balance.
The advantage of this model is that it is the only way of retaining
the theoretical attractiveness of k = 0 while changing the
age of the universe from the relation H0
t0 = 2/3, which characterises the
Einstein-de Sitter model. Since much observational
evidence indicates that H0 t0
must adjust to keep in balance.
The advantage of this model is that it is the only way of retaining
the theoretical attractiveness of k = 0 while changing the
age of the universe from the relation H0
t0 = 2/3, which characterises the
Einstein-de Sitter model. Since much observational
evidence indicates that H0 t0  1 (see chapter 5),
this model has received a good deal of interest in recent years.
To keep things simple we shall neglect radiation, so that
the Friedmann equation is
1 (see chapter 5),
this model has received a good deal of interest in recent years.
To keep things simple we shall neglect radiation, so that
the Friedmann equation is
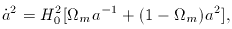
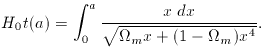
 m - 1| /
m - 1| /  m), which turns the integral into
m), which turns the integral into
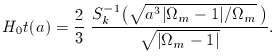
 m > 1,
otherwise sinh; these are still k = 0 models.
This t (a) relation is compared to models without
vacuum energy in figure 3.6.
Since there is nothing special about the current era, we can clearly
also rewrite this expression as
m > 1,
otherwise sinh; these are still k = 0 models.
This t (a) relation is compared to models without
vacuum energy in figure 3.6.
Since there is nothing special about the current era, we can clearly
also rewrite this expression as
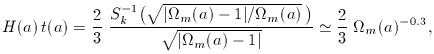
 m
m  0.1). In the general case of significant
0.1). In the general case of significant  but k
but k  0,
this expression still gives a very good approximation to the exact result,
provided
0,
this expression still gives a very good approximation to the exact result,
provided  m is
replaced by 0.7
m is
replaced by 0.7 m -
0.3
m -
0.3 v + 0.3
(Carroll, Press & Turner 1992).
v + 0.3
(Carroll, Press & Turner 1992).
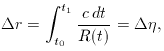
 , which the Friedmann equation says is
, which the Friedmann equation says is  dR / sqrt(
dR / sqrt( R2) at
early times. Thus, this integral converges if
R2) at
early times. Thus, this integral converges if
 R2
->
R2
->  as
t0 -> 0, otherwise it diverges.
Provided the equation of state is such that
as
t0 -> 0, otherwise it diverges.
Provided the equation of state is such that  changes faster than R-2, light
signals can only
propagate a finite distance between the big bang and the present;
there is then said to be a particle horizon.
Such a horizon therefore exists in conventional
big bang models, which are dominated by radiation at early times.
changes faster than R-2, light
signals can only
propagate a finite distance between the big bang and the present;
there is then said to be a particle horizon.
Such a horizon therefore exists in conventional
big bang models, which are dominated by radiation at early times.
 r diverges as t ->
r diverges as t ->  . If it does, then
seeing a given event is just a question of waiting long enough.
Clearly, an event horizon requires R (t) to increase more quickly than
t, so that distant parts of the universe recede ``faster than light''.
This does not occur unless the universe is dominated by vacuum energy at
late times, as discussed above.
Despite this distinction, cosmologists usually
say the horizon when they mean the particle horizon.
. If it does, then
seeing a given event is just a question of waiting long enough.
Clearly, an event horizon requires R (t) to increase more quickly than
t, so that distant parts of the universe recede ``faster than light''.
This does not occur unless the universe is dominated by vacuum energy at
late times, as discussed above.
Despite this distinction, cosmologists usually
say the horizon when they mean the particle horizon.
 , at which
point the conformal time
, at which
point the conformal time  = 2
= 2  also (from above)
and the model has recollapsed. Since we live in an expanding
universe, it is not even possible
to see the same object in two different directions, at
radii r and 2
also (from above)
and the model has recollapsed. Since we live in an expanding
universe, it is not even possible
to see the same object in two different directions, at
radii r and 2  -
r. This requires a horizon size
larger than
-
r. This requires a horizon size
larger than  ; but conformal time
; but conformal time  =
=  is attained
only at maximum expansion, so antipodal pairs of high-redshift
objects are visible only in the collapse phase.
These constraints do not apply if
the universe has a significant cosmological constant;
loitering models should allow one to see antipodal pairs
at approximately the same redshift. This effect
has been sought, but without success.
is attained
only at maximum expansion, so antipodal pairs of high-redshift
objects are visible only in the collapse phase.
These constraints do not apply if
the universe has a significant cosmological constant;
loitering models should allow one to see antipodal pairs
at approximately the same redshift. This effect
has been sought, but without success.