


3.3 Structure Formation
The Friedmann-Lemaître model is unstable
to the gravitational growth of departures from a homogeneous mass
distribution. The present large-scale homogeneity could have
grown out of primeval chaos, but the initial conditions would
be absurdly special. That is, the Friedmann-Lemaître model
requires that the present structure - the clustering of mass in
galaxies and systems of galaxies - grew
out of small primeval departures from homogeneity. The
consistency test for an acceptable set of cosmological parameters
is that one has to be able to assign a physically sensible
initial condition that evolves into the present structure of the
universe. The constraint from this consideration in
line 3c is discussed by White et al.
[44], and in
line 3b by Bahcall et al.
([45],
[46]).
Here I explain the cautious ratings in line 3a.
As has been widely discussed, it may be possible to read the
values of  and other
cosmological parameters from the spectrum of angular fluctuations of the CBR
([47] and
references therein). This assumes Nature has kept the evolution
of the early universe simple, however, and we have hit on
the right picture for its evolution. We may know in the next few
years. If the precision measurements of the CBR anisotropy from
the MAP and PLANCK satellites match in all detail the prediction
of one of the structure formation models now under discussion it
will compel acceptance. But meanwhile we should bear in mind
the possibility that Nature was not kind enough to have presented
us with a simple problem.
and other
cosmological parameters from the spectrum of angular fluctuations of the CBR
([47] and
references therein). This assumes Nature has kept the evolution
of the early universe simple, however, and we have hit on
the right picture for its evolution. We may know in the next few
years. If the precision measurements of the CBR anisotropy from
the MAP and PLANCK satellites match in all detail the prediction
of one of the structure formation models now under discussion it
will compel acceptance. But meanwhile we should bear in mind
the possibility that Nature was not kind enough to have presented
us with a simple problem.
An example of the possible ambiguity in the interpretation of the
present anisotropy measurements is shown in
Fig. 3. The two models
assume the same dynamical actors -cold dark matter (CDM),
baryons, three families of massless neutrinos, and the CBR - but
different initial conditions. In the adiabatic model the primeval
entropy per conserved particle number is homogeneous, the space
distribution of the primeval mass density fluctuations is a
stationary random process with the scale-invariant
spectrum  k, and the cosmological parameters
are
k, and the cosmological parameters
are  =
0.35,
=
0.35,  = 0.65, and h =
0.625 (following
[49]).
The isocurvature initial condition in the other model is that the
primeval mass distribution is homogeneous - there are no
curvature fluctuations - and structure formation is seeded by an
inhomogeneous composition. In the model
shown here the primeval entropy per baryon is homogeneous, to
agree with the standard model for light element production, and
the primeval distribution of the CDM has fluctuation spectrum
= 0.65, and h =
0.625 (following
[49]).
The isocurvature initial condition in the other model is that the
primeval mass distribution is homogeneous - there are no
curvature fluctuations - and structure formation is seeded by an
inhomogeneous composition. In the model
shown here the primeval entropy per baryon is homogeneous, to
agree with the standard model for light element production, and
the primeval distribution of the CDM has fluctuation spectrum
 (16)
(16)
The cosmological parameters are  = 0.2,
= 0.2,  = 0.8, and
h = 0.7. The lower density parameter produces a more
reasonable-looking cluster mass function for the
isocurvature initial condition
[50].
In both models the density parameter in baryons is
= 0.8, and
h = 0.7. The lower density parameter produces a more
reasonable-looking cluster mass function for the
isocurvature initial condition
[50].
In both models the density parameter in baryons is
 B = 0.03, the rest
of
B = 0.03, the rest
of  is in CDM, and space
sections are flat (
is in CDM, and space
sections are flat ( = 1 -
= 1 -
 ).
Both models are normalized to the large-scale
galaxy distribution. The adiabatic initial condition follows
naturally from inflation,
as a remnant of the squeezed field that drove the rapid
expansion. A model for the isocurvature condition assumes the CDM
is (or is the remnant of) a massive scalar field that was in the
ground level during inflation and became squeezed to a classical
realization. In the simplest models for inflation this produces
m = -3 in Eq. (16). The tilt to m = -1.8 requires only
modest theoretical ingenuity
[51].
That is, both models
have pedigrees from commonly discussed early universe physics.
).
Both models are normalized to the large-scale
galaxy distribution. The adiabatic initial condition follows
naturally from inflation,
as a remnant of the squeezed field that drove the rapid
expansion. A model for the isocurvature condition assumes the CDM
is (or is the remnant of) a massive scalar field that was in the
ground level during inflation and became squeezed to a classical
realization. In the simplest models for inflation this produces
m = -3 in Eq. (16). The tilt to m = -1.8 requires only
modest theoretical ingenuity
[51].
That is, both models
have pedigrees from commonly discussed early universe physics.
The lesson from Fig. 3 is that at least two families
of models, with different relations between  and the
value of l at the peak, come close to the measurements of the
CBR fluctuation spectrum, within the still substantial
uncertainties. An estimate of
and the
value of l at the peak, come close to the measurements of the
CBR fluctuation spectrum, within the still substantial
uncertainties. An estimate of  from the CBR
anisotropy measurements thus may depend on the choice of the
model for structure formation. Programs of measurement of
from the CBR
anisotropy measurements thus may depend on the choice of the
model for structure formation. Programs of measurement of
 Tl in
progress should be capable of
distinguishing between the adiabatic and isocurvature models,
even given the freedom to adjust the shape of P (k).
The interesting possibility is that
some other model for structure formation with a very different
value of
Tl in
progress should be capable of
distinguishing between the adiabatic and isocurvature models,
even given the freedom to adjust the shape of P (k).
The interesting possibility is that
some other model for structure formation with a very different
value of  may give an even
better fit to the improved measurements.
may give an even
better fit to the improved measurements.
I assign a failing grade to the Einstein-de Sitter model in line
3a because the adiabatic and isocurvature models both prefer low
 ([52],
[53]).
I add question marks to indicate this still is a model-dependent result.
([52],
[53]).
I add question marks to indicate this still is a model-dependent result.



 and other
cosmological parameters from the spectrum of angular fluctuations of the CBR
([47] and
references therein). This assumes Nature has kept the evolution
of the early universe simple, however, and we have hit on
the right picture for its evolution. We may know in the next few
years. If the precision measurements of the CBR anisotropy from
the MAP and PLANCK satellites match in all detail the prediction
of one of the structure formation models now under discussion it
will compel acceptance. But meanwhile we should bear in mind
the possibility that Nature was not kind enough to have presented
us with a simple problem.
and other
cosmological parameters from the spectrum of angular fluctuations of the CBR
([47] and
references therein). This assumes Nature has kept the evolution
of the early universe simple, however, and we have hit on
the right picture for its evolution. We may know in the next few
years. If the precision measurements of the CBR anisotropy from
the MAP and PLANCK satellites match in all detail the prediction
of one of the structure formation models now under discussion it
will compel acceptance. But meanwhile we should bear in mind
the possibility that Nature was not kind enough to have presented
us with a simple problem.



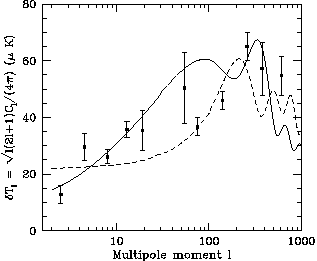
 =
=  / l is
(Tl)2, as
in Eqs. (5) to (7). Data are from the compilation by Ratra
/ l is
(Tl)2, as
in Eqs. (5) to (7). Data are from the compilation by Ratra
 k, and the cosmological parameters
are
k, and the cosmological parameters
are  = 0.65, and h =
0.625 (following
= 0.65, and h =
0.625 (following

 Tl in
progress should be capable of
distinguishing between the adiabatic and isocurvature models,
even given the freedom to adjust the shape of P (k).
The interesting possibility is that
some other model for structure formation with a very different
value of
Tl in
progress should be capable of
distinguishing between the adiabatic and isocurvature models,
even given the freedom to adjust the shape of P (k).
The interesting possibility is that
some other model for structure formation with a very different
value of