Einstein and de
Sitter (1932)
argued that the case
m = 1,
= 0, is a reasonable
working model: the low pressure matter term in
equation (6) is the only component one could be sure
is present, and the and
space curvature terms are not logically required in a relativistic expanding
universe.
Now everyone agrees that this Einstein-de Sitter model is the elegant case, because it has no characteristic time to compare to the epoch at which we have come on the scene. This, with the perception that the Einstein-de Sitter model offers the most natural fit to the inflation scenario for the very early universe, led to a near consensus in the early 1990s that our universe almost certainly is Einstein-de Sitter.
The arguments make sense, but not the conclusion. For the
reasons discussed in Section 4.1, it
seems to me exceedingly difficult to reconcile
m = 1 with the
dynamical evidence.
The paradigm has shifted, to a low density cosmologically flat universe, with
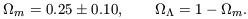
| (7) |
There still are useful cautionary discussions (Rowan-Robinson 2000), but the community generally has settled on these numbers. The main driver was not the dynamical evidence, but rather the observational fit to the adiabatic cold dark matter (CDM) model for structure formation (Ostriker & Steinhardt 1995).
I have mixed feelings about this. The low mass density model certainly makes sense from the point of view of dynamics (Bahcall et al. 2000; Peebles, Shaya & Tully 2000; and references therein). It is a beautiful fit to the new evidence from weak lensing and the SNeIa redshift-magnitude relation. But the paradigm shift was driven by a model for structure formation, and the set of assumptions in the model must be added to the list to be checked to complete the cosmological tests. I am driven by aspects of the CDM model that make me feel uneasy, as discussed next.