6. MEASURING _m

The present author, like many theorists, has long regarded the Einstein-de Sitter (_m = 1, = 0) cosmology as the most attractive one. For one thing, there are only three possible constant values for - 0, 1, and 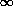- of which the only one that can describe our universe is _m = 1. Also, cosmic inflation is the only known solution for several otherwise intractable problems, and all simple inflationary models predict that the universe is flat, i.e. that _m + = 1. Since there is no known physical reason for a non-zero cosmological constant, it was often said that inflation favors = 1. Of course, theoretical prejudice is not a reliable guide. In recent years, many cosmologists have favored _m ~ 0.3, both because of the H₀ - t₀ constraints and because cluster and other relatively small-scale measurements have given low values for _m. (For a summary of arguments favoring low _m 0.2 and = 0, see Coles & Ellis (1997). A review that notes that larger scale measurements favor higher _m is Dekel, Burstein, & White 1997.) But the most exciting new evidence has come from cosmological-scale measurements.

Type Ia Supernovae. At present, the most promising techniques for measuring _m and on cosmological scales use the small-angle anisotropies in the CMB radiation and high-redshift Type Ia supernovae (SNe Ia). We will discuss the latter first. SNe Ia are the brightest supernovae, and the spread in their intrinsic brightness appears to be relatively small. The Supernova Cosmology Project (Perlmutter et al. 1997a) demonstrated the feasibility of finding significant numbers of such supernovae. The first seven high redshift SNe Ia that they analyzed gave for a flat universe _m = 1 - = 0.94^+0.34_-0.28, or equivalently = 0.06^+0.28_-0.34 (< 0.51 at the 95% confidence level) (Perlmutter et al. 1997a). But adding one z = 0.83 SN Ia for which they had good HST data lowered the implied _m to 0.6 ± 0.2 in the flat case (Perlmutter et al. 1998). Analysis of their larger dataset of 42 high-redshift SNe Ia gives for the flat cast _m = 0.28^{+0.09 +0.05}_{-0.08 -0.04} where the first errors are statistical and the second are identified systematics (Perlmutter et al. 1999). The High-Z Supernova team has also searched successfully for high-redshift supernovae to measure _m (Garnavich et al. 1997, Riess et al. 1998), and their three HST SNe Ia, two at z 0.5 and one at 0.97, imply _m = 0.4 ± 0.3 in the flat case. The main concerns about the interpretation of this data are evolution of the SNe Ia (Drell, Loredo, & Wasserman 1999) and dimming by dust. A recent specific supernova evolution concern that was discussed at this workshop is that the rest frame rise-times of distant supernovae may be longer than nearby ones (Riess et al. 1999). But a direct comparison between nearby supernova and the SCP distant sample shows that they are rather consistent with each other (Aldering, Nugent, & Knop 1999). Ordinary dust causes reddening, but hypothetical grey dust would cause much less reddening and could in principle provide an alternative explanation for the fact that high-redshift supernovae are observed to be dimmer than expected in a critical-density cosmology. It is hard to see why the largest dust grains, which would be greyer, should preferentially be ejected by galaxies (Simonsen & Hannestad 1999). Such dust, if it exists, would also absorb starlight and reradiate it at long wavelengths, where there are other constraints that could, with additional observations, rule out this scenario (Aguirre & Haiman 1999). But another way of addressing this question is to collect data on supernovae with redshift z > 1, where the dust scenario predicts considerably more dimming than the cosmology. The one z > 1 supernova currently available, SCP's ``Albinoni'' (SN1998eq) at z = 1.2, will help, and both the SCP and the High-Z group are attempting to get a few more very high redshift supernovae.

CMB anisotropies. The location of the first Doppler (or acoustic, or Sakharov) peak at angular wavenumber l 250 indicated by the presently available data (Scott, this volume) is evidence in favor of a flat universe _m + 1. New data from the MAXIMA and BOOMERANG balloon flights apparently confirms this, and the locations of the second and possibly third peak appear to be consistent with the predictions (Hu, Spergel, & White 1997) of simple cosmic inflation theories. Further data should be available in 2001 from the NASA Microwave Anisotropy Probe satellite.

Large-scale Measurements. The comparison of the IRAS redshift surveys with POTENT and related analyses typically give values for the parameter _{I m}^0.6 / b_I (where b_I is the biasing parameter for IRAS galaxies), corresponding to 0.3 _m 3 (for an assumed b_I = 1.15). It is not clear whether it will be possible to reduce the spread in these values significantly in the near future - probably both additional data and a better understanding of systematic and statistical effects will be required. A particularly simple way to deduce a lower limit on _m from the POTENT peculiar velocity data was proposed by Dekel & Rees (1994), based on the fact that high-velocity outflows from voids are not expected in low- models. Data on just one nearby void indicates that _m 0.3 at the 97% C.L. Stronger constraints are available if we assume that the probability distribution function (PDF) of the primordial fluctuations was Gaussian. Evolution from a Gaussian initial PDF to the non-Gaussian mass distribution observed today requires considerable gravitational nonlinearity, i.e. large _m. The PDF deduced by POTENT from observed velocities (i.e., the PDF of the mass, if the POTENT reconstruction is reliable) is far from Gaussian today, with a long positive-fluctuation tail. It agrees with a Gaussian initial PDF if and only if _m ~ 1; _m < 1 is rejected at the 2 level, and _m 0.3 is ruled out at 4 (Nusser & Dekel 1993; cf. Bernardeau et al. 1995). It would be interesting to repeat this analysis with newer data.

Measurements on Scales of a Few Mpc. A study by the Canadian Network for Observational Cosmology (CNOC) of 16 clusters at z ~ 0.3, mostly chosen from the Einstein Medium Sensitivity Survey (Henry et al. 1992), was designed to allow a self-contained measurement of _m from a field M / L which in turn was deduced from their measured cluster M / L. The result was _m = 0.19 ± 0.06 (Carlberg et al. 1997). These data were mainly compared to standard CDM models, and they appear to exclude _m = 1 in such models.

Estimates on Galaxy Halo Scales. Work by Zaritsky et al. (1993) has confirmed that spiral galaxies have massive halos. They collected data on satellites of isolated spiral galaxies, and concluded that the fact that the relative velocities do not fall off out to a separation of at least 200 kpc shows that massive halos are the norm. The typical rotation velocity of ~ 200-250 km s^-1 implies a mass within 200 kpc of ~ 2 x 10¹² M. A careful analysis taking into account selection effects and satellite orbit uncertainties concluded that the indicated value of _m exceeds 0.13 at 90% confidence (Zaritsky & White 1994), with preferred values exceeding 0.3. Newer data suggesting that relative velocities do not fall off out to a separation of ~ 400 kpc (Zaritsky et al. 1997) presumably would raise these _m estimates.

Cluster Baryons vs. Big Bang Nucleosynthesis. White et al. (1993) emphasized that X-ray observations of the abundance of baryons in clusters can be used to determine _m if clusters are a fair sample of both baryons and dark matter, as they are expected to be based on simulations (Evrard, Metzler, & Navarro 1996). The fair sample hypothesis implies that

(1)

We can use this to determine _m using the baryon abundance _b h² = 0.019 ± 0.001 from the measurement of the deuterium abundance in high-redshift Lyman limit systems, of which a third has recently been discovered (Kirkman et al. 1999). Using X-ray data from an X-ray flux limited sample of clusters to estimate the baryon fraction f_b = 0.075 h^-3/2 (Mohr, Mathiesen, & Evrard 1999) gives _m = 0.25 h^-1/2 = 0.3 ± 0.1 using h = 0.65 ± 0.08. Estimating the baryon fraction using Sunyaev-Zel'dovich measurements of a sample of 18 clusters gives f_b = 0.77 h^-1 (Carlstrom et al. 1999), and implies _m = 0.25 h^-1 = 0.38 ± 0.1.

Cluster Evolution. The dependence of the number of clusters on redshift can be a useful constraint on theories (e.g., Eke et al. 1996). But the cluster data at various redshifts are difficult to compare properly since they are rather inhomogeneous. Using just X-ray temperature data, Eke et al. (1998) conclude that _m 0.45 ± 0.2, with _m = 1 strongly disfavored.

Power Spectrum. In the context of the CDM class of models, two additional constraints are available. The spectrum shape parameter _m h 0.25 ± 0.05, implying _m 0.4 ± 0.1. A new measurement _m = 0.34 ± 0.1 comes from the amplitude of the power spectrum of fluctuations at redshift z ~ 3, measured from the Lyman forest (Weinberg et al. 1999). This result is strongly inconsistent with high-_m models because they would predict that the fluctuations grow much more to z = 0, and thus would be lower at z = 3 than they are observed to be.